[Paper Review] 25.(i2i translation) Image-to-Image translation with Conditional Adversarial Networks

[Paper Review] 25. Image-to-Image translation with Conditional Adversarial Networks

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Structured Losses for image modeling
   2. Conditional GANs
   3. Pix2Pix
4. Method
   1. Objective
   2. Network Architectures
   3. Optimization and Inference

0. Abstract

investigate CONDITIONAL adversarial networks

as a solution to image-to-image translation

Can be used to solve variety of tasks! ( below )

1. Introduction

explore GANs in conditional setting

\(\rightarrow\) “condition on INPUT IMAGE”

2. Related Work

1) Structured Losses for image modeling

image-to-image translation

• often formulated as per-pixel classification / regression
• learn a structured loss
  • penalize the “joint configuration of the output”

2) Conditional GANs

several other papers have also used GANs for image-to-image mapping…

but only applied the GAN “unCONDITIONALLY”

3) Pix2Pix

• generator : “U-net”

• discriminator : convolutional “PatchGAN” classifier

  ( only penalizes structure at the scale of image patches )

3. Method

GANs vs CGANs

• GANs = \(G : z \rightarrow y\)
• conditional GANs = \(G : {x,z} \rightarrow y\)

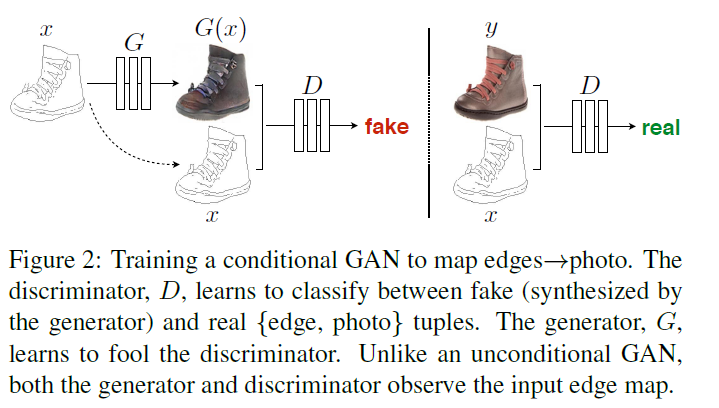
1) Objective

(a) objective of conditional GAN

• \(\mathcal{L}_{c G A N}(G, D)= \mathbb{E}_{x, y}[\log D(x, y)]+ \mathbb{E}_{x, z}[\log (1-D(x, G(x, z))]\).

(b) objective of original GAN

• \(\mathcal{L}_{G A N}(G, D)= \mathbb{E}_{y}[\log D(y)]+\mathbb{E}_{x, z}[\log (1-D(G(x, z))]\).

(c) L1 distance

• beneficial to mix GAN objective with more traditional loss
• L1 encourages less blurring than L2
• \(\mathcal{L}_{L 1}(G)=\mathbb{E}_{x, y, z}\left[ \mid \mid y-G(x, z) \mid \mid _{1}\right]\).

FINAL OBJECTIVE :

• \(G^{*}=\arg \min _{G} \max _{D} \mathcal{L}_{c G A N}(G, D)+\lambda \mathcal{L}_{L 1}(G)\).

without \(z\), can still learn mapping from \(x\) to \(y\)… BUT deterministic output!

\(\rightarrow\) provide noise only by dropout ( both at train + test )

BUT…minor stochasticity

2) Network Architectures

module :

• convolution - BatchNorm - ReLU

a) Generator with skips

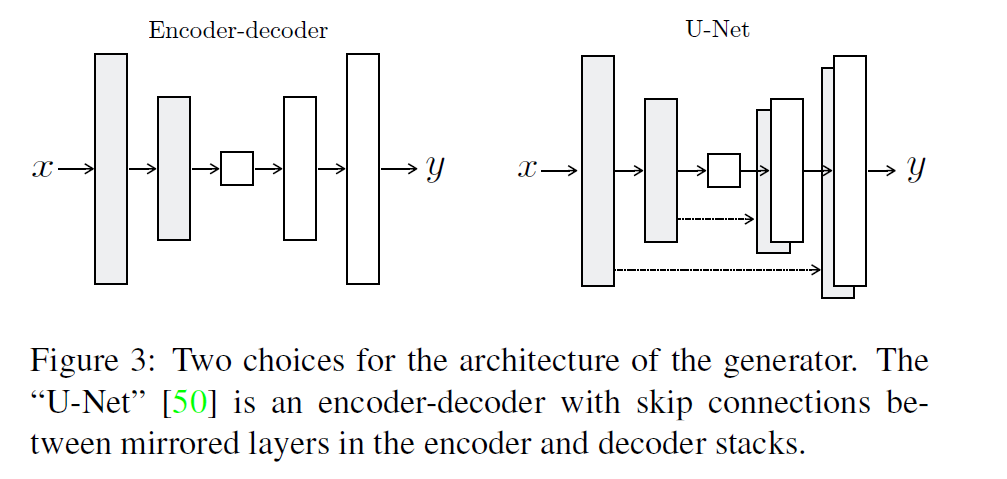
• add skip connections, following the general shape of a “U-Net”

b) Markovian discriminator (PatchGAN)

L1 & L2 loss : produce blurry results…

but in many cases, they capture low frequencies!

By using both…

• restrict \(D\) to only model high-frequency structure
• relying on an L1-term to force low-frequency correctness

3) Optimization and Inference

rather than training \(G\) to minimize \(\log (1-D(x, G(x, z))\)…

maximize \(\log D(x, G(x, z))\) !

At inference time…

• apply BN using stat of test batch, rathern than training batch