[Paper Review] 29.(i2i translation) StarGAN v2 ; Diverse Image Synthesis for Multiple Domains

[Paper Review] 29. StarGAN v2 : Diverse Image Synthesis for Multiple Domains

Contents

1. Abstract
2. Introduction
3. StarGAN v2
   1. Proposed Framework
   2. Training Objectives

0. Abstract

good image-to-image translation model :

• property 1) diversity of generated images
• property 2) scalability over multiple domains

1. Introduction

to address scalability, StarGAN has been rpoposed

• learns the mappings between all available domains, using only SINGLE generator

  • takes “domain label” as an additional input
  • then, learns to transform an image into the corresponding domain

• problem

  • deterministic mapping

    ( does not capture multi-modal nature of data distn )

StarGAN v2

• a scalable approach, that can generate DIVERSE images across MULTIPLE domains
• can represent “diverse styles of a specific domains”

2. StarGAN v2

describe

• 1) proposed framework
• 2) training objective functions

1) Proposed Framework

Goal : train a SINGLE \(G\) that can generate diverse images of each domain \(y\) that corresponds to the image \(x\)

• generate domain-specific style vectors

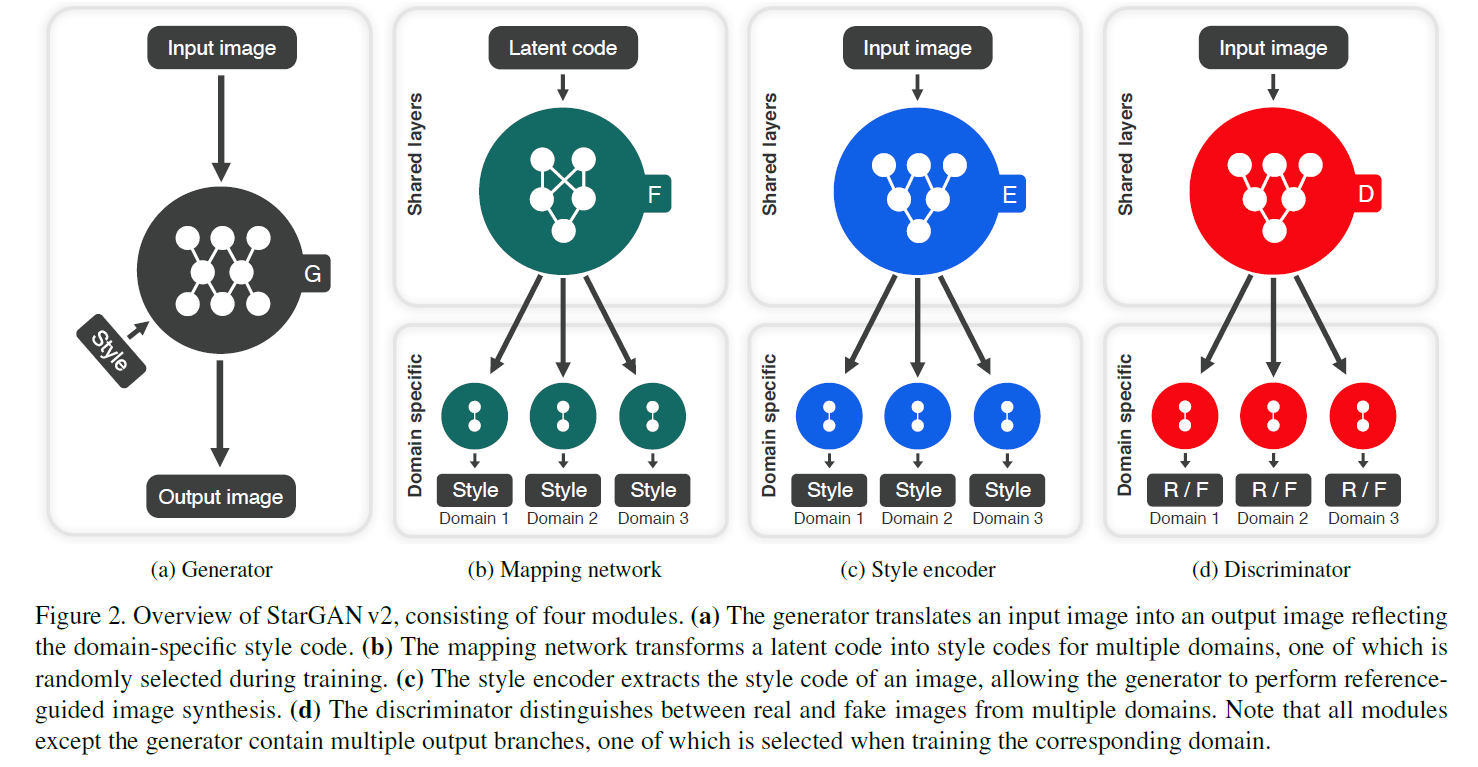
[ a. Generator, \(G\) ]

• input : \(x\)

• output : \(G(x,s)\)

  ( reflecting specific style code \(s\) , provided by…. mapping network \(F\) or style encoder \(E\) )

[ b. Mapping Network, \(F\) ]

• input : latent code \(\mathbf{z}\) & domain \(y\)

• output : \(s=F_y(\mathbf{z})\)

• consists of MLP, with multiple output branches,

  to provide style codes for all available domains

[ c. Style Encoder, \(E\) ]

• input : \(x\) & corresponding domain \(y\)
• output : \(s= E_y(x)\)
• goal : extract the style code of \(x\)

[ d. Discriminator, \(D\) ]

• learns a binary classification
• determine whether \(x\) is …
  • real image of its domain \(y\)
  • fake image \(G(x,s)\)

2) Training Objectives

[ a. Adversarial objective ]

• generate a target style code \(\widetilde{\mathbf{s}}=F_{\widetilde{y}}(\mathbf{z})\)
• \(\mathcal{L}_{a d v}= \mathbb{E}_{\mathbf{x}, y}\left[\log D_{y}(\mathbf{x})\right]+ \mathbb{E}_{\mathbf{x}, \widetilde{y}, \mathbf{z}}\left[\log \left(1-D_{\widetilde{y}}(G(\mathbf{x}, \widetilde{\mathbf{s}}))\right)\right]\).

[ b. Style Reconstruction ]

• \(\mathcal{L}_{s t y}=\mathbb{E}_{\mathbf{x}, \widetilde{y}, \mathbf{z}}\left[\left \mid \mid \widetilde{\mathbf{s}}-E_{\widetilde{y}}(G(\mathbf{x}, \widetilde{\mathbf{s}}))\right \mid \mid _{1}\right]\).

[ c. Style Diversification ]

• enable \(G\) to produce diverse images!

• regularize \(G\) with “diversity sensitive loss”

• \(\mathcal{L}_{d s}=\mathbb{E}_{\mathbf{x}, \widetilde{y}, \mathbf{z}_{1}, \mathbf{z}_{2}}\left[\left \mid \mid G\left(\mathbf{x}, \widetilde{\mathbf{s}}_{1}\right)-G\left(\mathbf{x}, \widetilde{\mathbf{s}}_{2}\right)\right \mid \mid _{1}\right]\).

  • where target style codes \(\widetilde{\mathbf{s}}_{1}\) and \(\widetilde{\mathbf{s}}_{2}\) :

    produced by \(F\) conditioned on two random latent codes \(\mathbf{z}_{1}\) and \(\mathbf{z}_{2}\)

[ d. Cycle consistency loss ]

• preserve source characteristics

• guarantee that the genrated image \(G(x,\tilde{s})\) preserves domain invariant characteristics of its input images \(x\)

• \(\mathcal{L}_{c y c}=\mathbb{E}_{\mathbf{x}, y, \widetilde{y}, \mathbf{z}}\left[ \mid \mid \mathbf{x}-G(G(\mathbf{x}, \widetilde{\mathbf{s}}), \hat{\mathbf{s}}) \mid \mid _{1}\right]\).

[ e. Full Objective ]

• \(\min _{G, F, E} \max _{D} \mathcal{L}_{a d v}+\lambda_{s t y} \mathcal{L}_{s t y} -\lambda_{d s} \mathcal{L}_{d s}+\lambda_{c y c} \mathcal{L}_{c y c}\).