[Paper Review] 04.Improved Precision and Recall Metric for Assessing Generative ModelsPermalink

ContentsPermalink

1. Abstract
2. Introduction
3. Precision & Recall
4. Improved Precision & Recall using kNN

0. AbstractPermalink

estimate the quality and coverage of the samples produced by generative model is important!

propose an EVALUATION metric, that can..

• separately & reliably measure BOTH of theses aspects
• by forming explicit, non-parametric representations of the manifolds of real & generated data

1. IntroductionPermalink

goal of generative methods : learn the MANIFOLD of training data

( so that we can subsequently generate novel samples, that are INDISTINGUISHABLE from training set )

when modeling complex manifold… 2 separate goals :

• 1) individual samples drawn from the model should be faithful to the examples ( =high quality )
• 2) variations should match that observed in the training set

widely used metric :

• FID(Frechet Inception Distance), IS(Inception Score), KID(Kernel Inception Distance)
• precision & recall

Precision : average sample quality of the sample distribution

Recall : coverage of the sample distribution

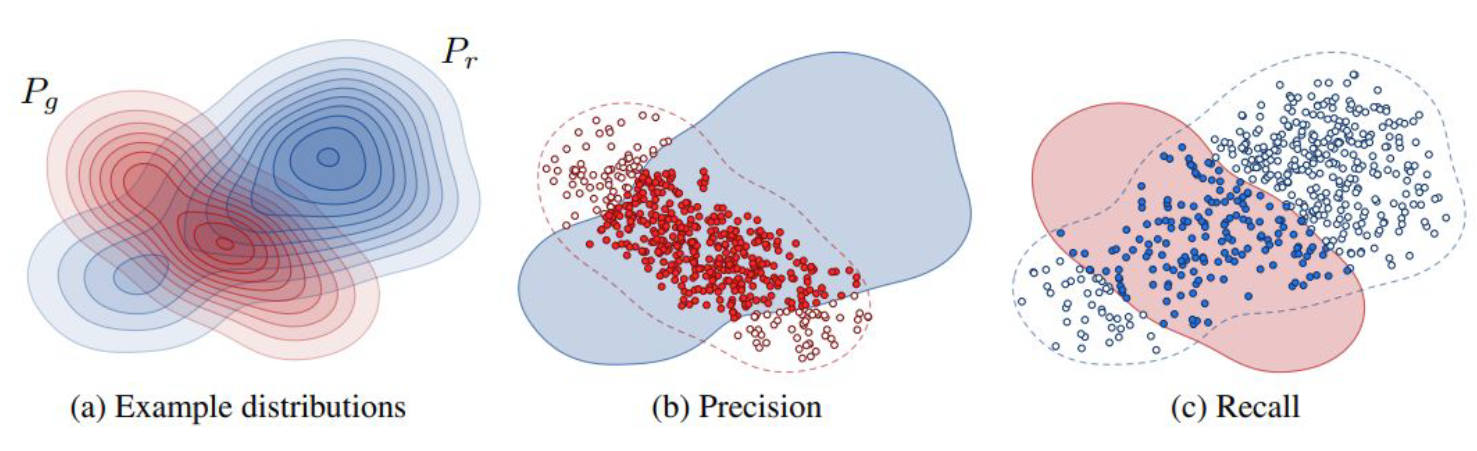
2. Precision & RecallPermalink

Precision

• = (REAL의 support에 빠진 FAKE) / (전체 FAKE)
• 직관적 이해 : fraction of generated images that are realistic

Recall

• = (FAKE의 support에 빠진 REAL) / (전체 REAL)
• 직관적 이해 : fraction of training data manifold covered by the generator

3. Improved Precision & Recall using kNNPermalink

key idea : form explicit non-parametric representations of the manifolds of real & generated data

• $X_{r} \sim P_{r}$ & $X_{g} \sim P_{g}$

embed both into high-dimensional feature space using a pre-trained classifier network

• becomes feature vectors by $\mathbf{\Phi}_{r}$ and $\mathbf{\Phi}_{g}$
• take an equal number of samples from each distribution ( $\mid \mathbf{\Phi}_{r} \mid = \mid \mathbf{\Phi}_{g} \mid$ )

For each set of feature vectors $\boldsymbol{\Phi} \in\left\{\boldsymbol{\Phi}_{r}, \mathbf{\Phi}_{g}\right\}$, estimate the corresponding manifold in the feature space

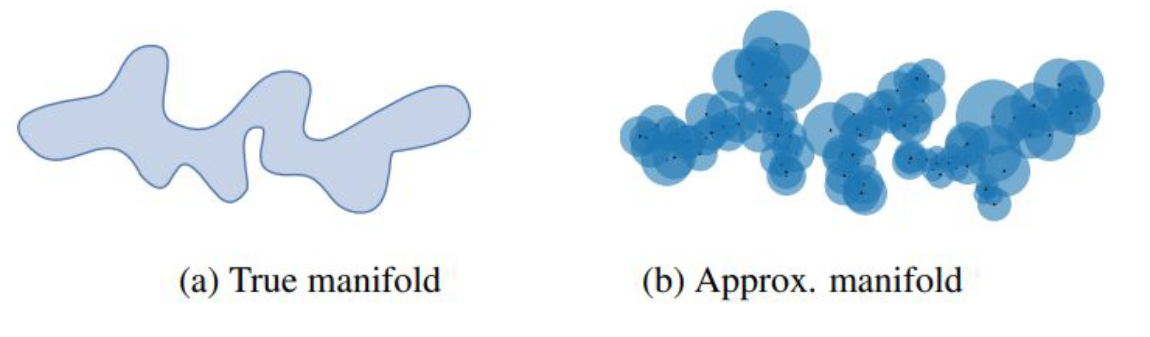
• approximate true manifold using k-NN radi

To determine whether a given sample $\phi$ is located within this volume….

define a binary function

$f(\boldsymbol{\phi}, \boldsymbol{\Phi})=\left\{\begin{array}{l} 1, \text { if } \mid \mid \boldsymbol{\phi}-\boldsymbol{\phi}^{\prime} \mid \mid _{2} \leq \mid \mid \boldsymbol{\phi}^{\prime}-\mathrm{NN}_{k}\left(\boldsymbol{\phi}^{\prime}, \mathbf{\Phi}\right) \mid \mid _{2} \text { for at least one } \phi^{\prime} \in \mathbf{\Phi} \\ 0, \text { otherwise } \end{array}\right.$.

New Metric using kNNPermalink

$\operatorname{precision}\left(\mathbf{\Phi}_{r}, \mathbf{\Phi}_{g}\right)=\frac{1}{ \mid \mathbf{\Phi}_{g} \mid } \sum_{\boldsymbol{\phi}_{g} \in \boldsymbol{\Phi}_{g}} f\left(\boldsymbol{\phi}_{g}, \mathbf{\Phi}_{r}\right) \quad \operatorname{recall}\left(\mathbf{\Phi}_{r}, \mathbf{\Phi}_{g}\right)=\frac{1}{ \mid \mathbf{\Phi}_{r} \mid } \sum_{\boldsymbol{\phi}_{r} \in \mathbf{\Phi}_{r}} f\left(\boldsymbol{\phi}_{r}, \mathbf{\Phi}_{g}\right)$.