[Paper Review] 07.(improved gan training)Which Training Methods for GANs do actually Converge?

[Paper Review] 07.Which Training Methods for GANs do actually Converge?

Contents

1. Abstract
2. Introduction
3. Instabilities in GAN training
   1. Background
   2. The Dirac-GAN
   3. Where do instabilities come from?
4. Regularization strategies
   1. WGAN
   2. Instance noise
   3. Zero-centered gradient penalties

0. Abstract

for local convergence of GAN training…

\(\rightarrow\) show that requirement of ABSOLUTE CONTINUITY is necessary

Introduces..

• 1) in case of distn that are NOT absolutely continuous…

  \(\rightarrow\) unregularized GAN is not always convergent

• 2) discuss regularization strategies to stabilize training

  • ex) instance noise
  • ex) zero-centered gradient penalties

1. Introduction

GD based GAN optimization : does not lead to convergence!

Assumption of absolute continuity

• not true for common use cases of GANs

This paper shows ….

[1] that this assumption is necessary!

• via simple yet prototypical example

  unregularized GAN training is NOT ALWAYS locally convergent

[2] how recent techniques for stabilizing GAN training affect local convergence on our example problem

Contributions

• 1) identify a simple yet prototypcal counter example,

  showing that (unregularized) GD based GAN optimization is NOT ALWAYS locally convergent

• 2) introduce REGULARIZATION techniques stabilize training

• 3) simplified gradient penalties

2. Instabilities in GAN training

(1) Background

• min-max two player game
• discriminator \(D_{\psi}(x)\) & generator \(G_{\theta}(z)\)
• training objective ( notation of Nagarajan & Kolter, 2017 )
  • \(L(\theta, \psi)=\mathrm{E}_{p(z)}\left[f\left(D_{\psi}\left(G_{\theta}(z)\right)\right)\right] +\mathrm{E}_{p_{\mathcal{D}}(x)}\left[f\left(-D_{\psi}(x)\right)\right]\).
  • \(f(t)=-\log (1+\exp (-t))\).
• usually trained using..
  • SimGD ( Simultaneous GD )
  • AltGD ( Alternating GD )

Local Convergence of GAN

• can be analyzed by looking at the spectrum of Jacobian \(F_{h}^{\prime}\left(\theta^{*}, \psi^{*}\right)\).
• if \(F_{h}^{\prime}\left(\theta^{*}, \psi^{*}\right)\) …
  • has eigenvalues with absolute value bigger than 1 :
    • will generally not converge to \(\left(\theta^{*}, \psi^{*}\right)\)
  • all eigenvalues have absolute value smaller than 1 :
    • will converge to \(\left(\theta^{*}, \psi^{*}\right)\) with linear rate \(\mathcal{O}\left( \mid \lambda_{\max } \mid ^{k}\right)\).

(2) The Dirac-GAN

show that UNregularized GAN training is neither locally/globally convergent

Dirac-GAN consists of

• [generator] univariate generator distn … \(p_{\theta}=\delta_{\theta}\)
• [discriminator] linear discriminator … \(D_{\psi}(x)=\psi \cdot x\).
• true data distn \(p_D\) : Dirac-distn concentrated at 0

GAN training objective

• \(L(\theta, \psi)=f(\psi \theta)+f(0)\).

\(\rightarrow\) do not converge in this SIMPLE setup!

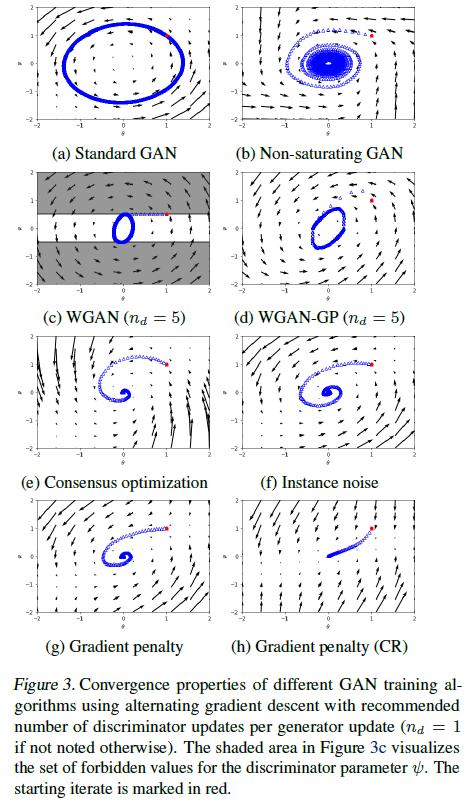
(3) Where do instabilities come from?

have to take a closer look at oscillatory behavior that GANs exhibit both for Dirac-GAN & for more complex systems

\(\rightarrow\) can be understood with figure below (1-b)

• process repeats indefinitely, does not converge

3. Regularization strategies

unregularized GAN training does not always converge to Nash-equilibrium

\(\rightarrow\) discuss how several regularization techniques influence convergence of Dirac-GAN

(1) WGAN

divergence of distributions

• (before) Hensen-Shannon
• (after) Wasserstein

even for absolutely continuous densities & infinitesimal lr…

WGANs are not always locally convergent

(2) Instance noise

add instance noise ( i.e independent Gaussian noise ) to data points

when using Gaussian instance noise with std \(\sigma\)…

• eigenvalues of Jacobian of the gradient vector field are…

  \(\lambda_{1 / 2}=f^{\prime \prime}(0) \sigma^{2} \pm \sqrt{f^{\prime \prime}(0)^{2} \sigma^{4}-f^{\prime}(0)^{2}}\).

(3) Zero-centered gradient penalties

eigenvalues of Jacobian of gradient vector filed for gradient-regularized Dirac-GAN at equilibrium point…

• \(\lambda_{1 / 2}=-\frac{\gamma}{2} \pm \sqrt{\frac{\gamma^{2}}{4}-f^{\prime}(0)^{2}}\).