(CS224W) 1.Introduction ; ML for Graphs

[ 1. Introduction : ML for Graphs ]

( 참고 : CS224W: Machine Learning with Graphs )

Contents

• 1-1. Why Graphs

• 1-2. Applications of Graph ML

• 1-3. Choice of Graph Representation

1-1. Why Graphs

1) Graphs

= general language for describing & analyzing entities with…

• 1) “relations”
• 2) “interactions”

Lots of data are “graphs”!

• ex) computer network, event graphs,…

2) Types of networks & graphs

Networks ( = Natural Graphs )

• 1) Social networks ( society )
• 2) Communication & Transactions
• 3) Biomedicine ( ex. genes )
• 4) Brain connections ( ex. thoughts )

Graphs ( = representation )

• 1) information/knowledge
• 2) similarity networks
• 3) relational structures

Relational Graphs

• model better relationships between entities!

• use DL for complex modeling

3) Networks are complex

Why is it complex?

• arbitrary size & complex structure
• no fixed node ordering or reference point
• dynamic & multi-modal features

4) DL in graphs

[ Input ]

• Network

[ Output ] (Prediction)

• 1) node labels
• 2) new links
• 3) generated graphs / subgraphs

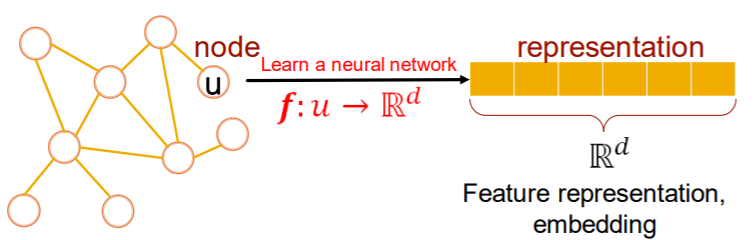
Key point : “Representation Learning”

• “automatically” learn features with DNN

• map to \(d\)-dim embeddings

  • similar nodes = similar in embedded space

5) Outline

• 1) Traditional methods
  • Graphlets, Graph Kernels
• 2) Node Embeddings
  • DeepWalk, Node2vec
• 3) GNN
  • GCN, GraphSAGE, GAT
• 4) Knowledge graph & reasoning
  • TransE, BetaE

• 5) Deep Generative models ( for graphs )

• 6) Applications

1-2. Applications of Graph ML

1) Diverse Tasks

• 1) Node classification
  • ex) categorizing users/items
• 2) Link prediction
  • ex) knowledge graph completion
• 3) Graph Classification
  • ex) Molecule property prediction
• 4) Clustering
  • ex) community detection
• 5) etc
  • Graph generation, Graph evolution ..

Diverse level of tasks

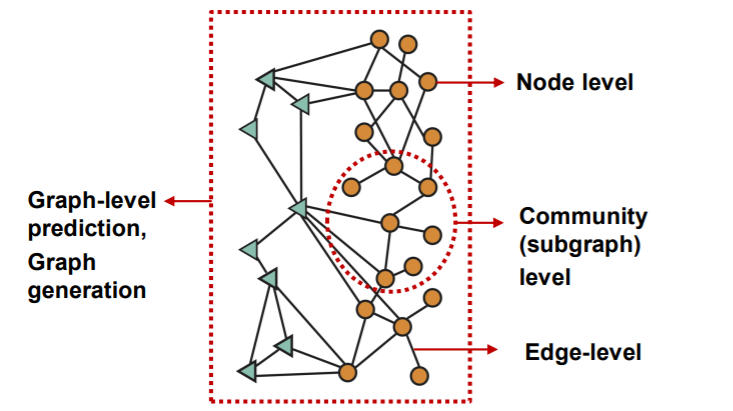
2) Example of “NODE-level” ML

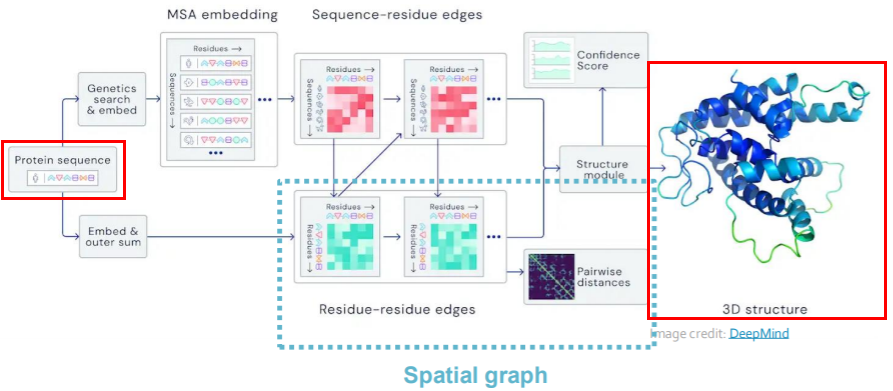
ex) Protein Folding

• Protein
  • protein= sequence of amino acid
  • 3d structure
  • interact with each other
• Goal : “predict 3D structure”, based on “amino acid sequence”
• key idea of AlphaFold : “spatial graph”
  • (1) node : amino acids
  • (2) edges : proximity between nodes

3) Example of “EDGE-level” ML

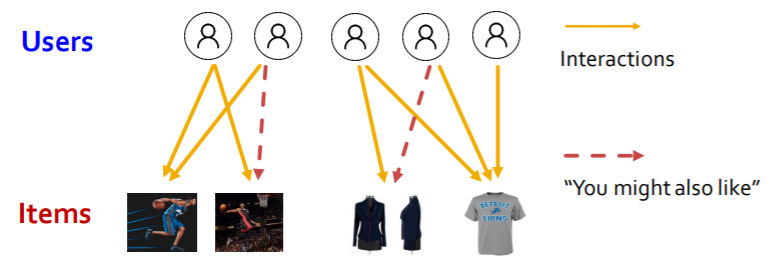
ex) Recommender Systems

• Formulation
  • (1) node : user & items
  • (2) edge : user & item interaction

• Goal : “Recommend item to users”

  ( predict whether 2 nodes are related )

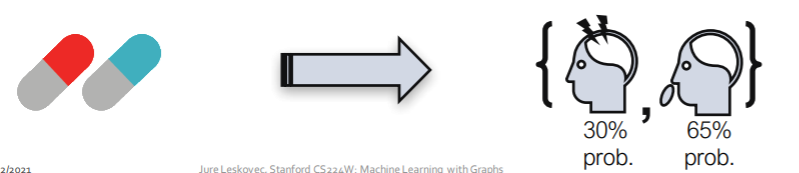
ex) Drug Side Effects

• Background : many patients & many drugs

• Goal : predict adverse side effects of “pair of drugs”

• Formulation
  • (1) node : drugs & proteins
  • (2) edges : interactions
    • drug-protein interaction
    • protein-protein interaction
    • drug-drug interaction

4) Example of “SUBGRAPH-level” ML

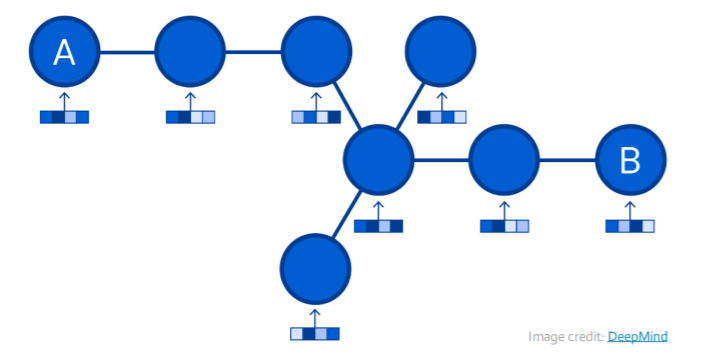
ex) Traffic Prediction

• want to move from A to B…. how long will it take?
• Formulation
  • (1) node : road segments
  • (2) edges : connectivity between nodes
• ex) Google Maps : traffic prediction with GNN

5) Examples of “GRAPH-level” ML

ex) Drug Discovery

• Antibiotics = small molecular graphs
• Formulation
  • (1) node : atoms
  • (2) edges : chemical bonds
• (Q) Which molecules should be prioritized?
• ex) graph classification model
  • predict promising molecules among candidates

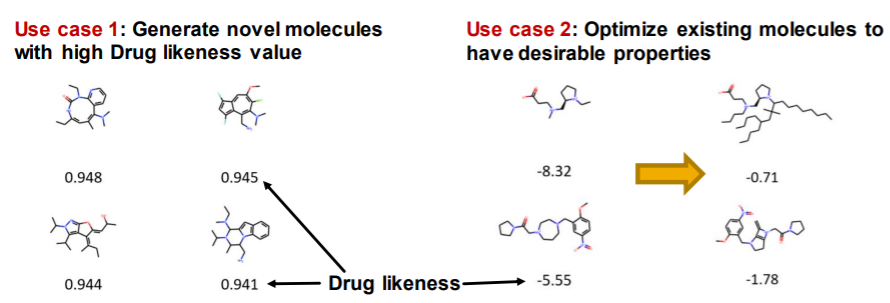
ex) Graph generation

• generate novel molecules ( new structure )
  • with “high drug likeness”
  • with “desirable properties”

ex) Physics Simulation

• Formulation
  • (1) node : particles
  • (2) edges : interaction between nodes
• Goal : predict how a graph will EVOLVE

1-3. Choice of Graph Representation

1) Components of Network

• (1) Objects : nodes, vertices ( notation : \(N\) )

• (2) Interactions : links, edges ( notation : \(E\) )

• (3) System : network, graph ( notation : \(G(N,E)\) )

Notation :

• \(\mid N \mid\) : number of nodes
• \(\mid E \mid\) : number of edges

[ Question ]

Which one is proper representation??

How to build a graph?

• 1) what are nodes?
• 2) what are edges?

[ Answer ]

• differ by domain/tasks!

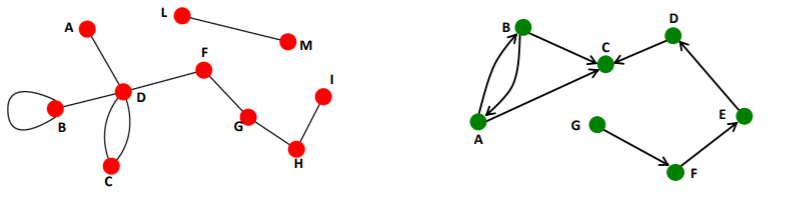
2) Directed & Undirected Graphs

Directed

• links = arcs
• ex) phone calls, following in INSTAGRAM

Undirected

• links = symmetrical, reciprocal
• ex) collaborations, friendship in FB

3) Node Degree

Node degree ( \(k_i\) )

• # of edges, adjacent to node \(i\)

Average degree

• \(\bar{k}=\langle k\rangle=\frac{1}{N} \sum_{i=1}^{N} k_{i}=\frac{2 E}{N}\).

Directed Network

In-degree & Out-degree

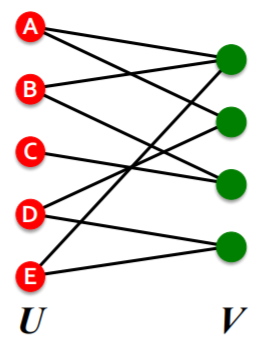
4) Bipartite Graph

graph, whose nodes can be divided into “2 disjoint sets \(U\), \(V\)”, where …

every link connects a node in \(U\) to one in \(V\)

( = \(U\) & \(V\) : independent sets )

ex) User-Movie rating

Folded / Projected Bipartite Graphs

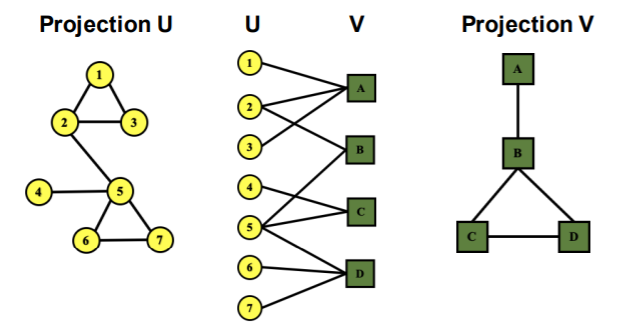
5) Adjacency Matrix

Different ways of representing graphs :

• 1) adjacency matrix

• 2) edge list & adjacency list

Adjacency Matrix

\(n \times n\) matrix ( \(n\) : number of nodes )

• connected = 1
• disconnected = 0

( Undirected Graph : symmetric adjacency matrix )

Problem : Adjacency matrices are SPARSE!

6) Edge list & Adjacency list

Different ways of representing graphs :

• 1) adjacency matrix

• 2) edge list & adjacency list

(a) Edge list

• ex) (2,3), (2,4), (3,2), (3,4) ,… (5,2)

(b) Adjacency list

• easier when network is large & sparse
• ex)
  • 1 :
  • 2 : 3,4
  • 3 : 2,4
  • 4 : 5
  • 5 : 1,2

7) Node & Edge ATTRIBUTES

ex) weight, ranking, type, sign, …

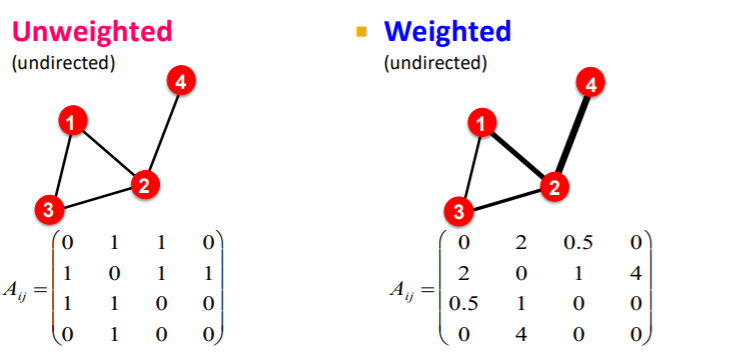
8) More Types of Graphs

unweighted & weighted

• unweighted ( 1 or 0 )
• weighted ( not binary )

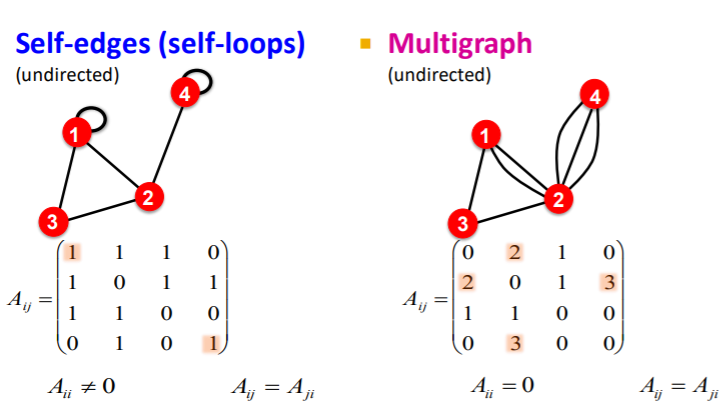
self-edges & multi-graph

• self-edges ( self-loops )
• multi-graph
  • multiple edges between pair of nodes

connected & disconnected graph

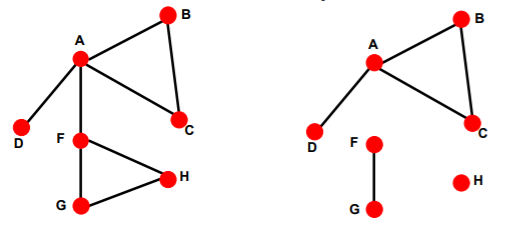
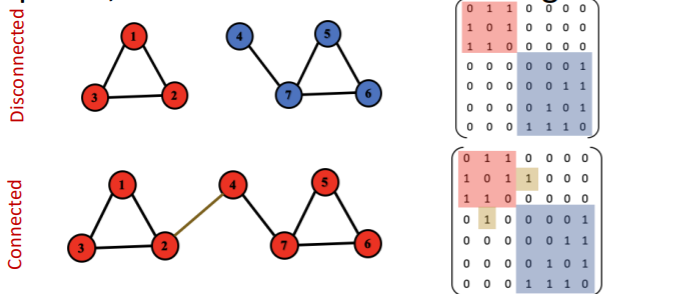
strongly & weakly connected graph

• strongly : both A-B & B-A path
• weakly : disregard edge direction

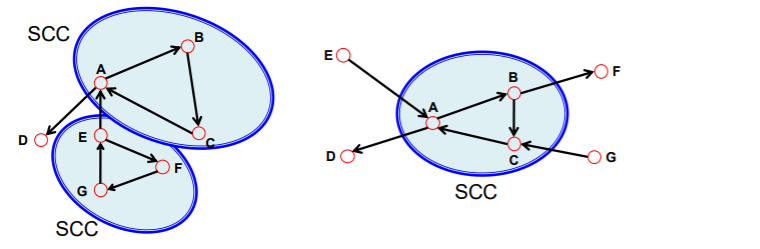
Strongly connected components (SCCs)