(CS224W) 11.Reasoning over Knowledge Graphs

[ 11. Reasoning over Knowledge Graphs ]

( 참고 : CS224W: Machine Learning with Graphs )

Contents

• Review
• 11-1. Reasoning in KG
• 11-2. Answering Predictive Queries
• 11-3. Query2Box

Review

Knowledge Graph (KG) Completion

• H : head / R : relation / T :tail

• goal : given (H,R), predict T

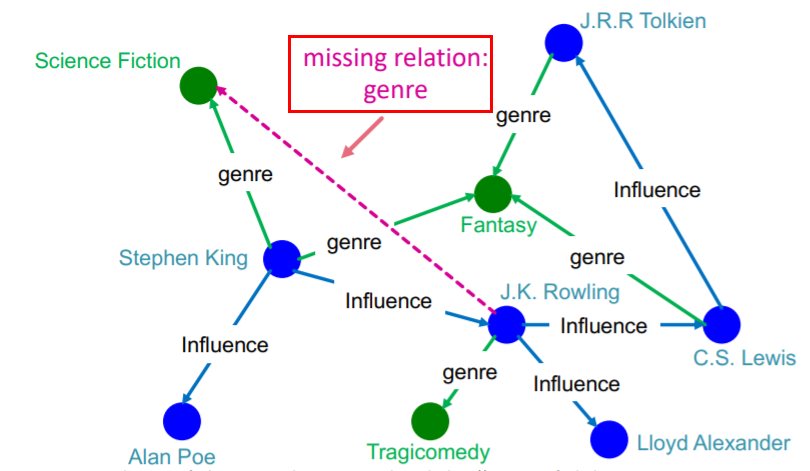
• example )

  • H : “J.K.Rowling”
  • R : “genre”
  • T: “Science Fiction”

11-1. Reasoning in KG

Question : how to perform “MULTI-hop” reasoning over KGs?

Reasoning over KG

1. Answering multi-hop queries
   1. Path queries
   2. Conjunctive queries
2. Query2Box

Task : how to do multi-hop reasoning ( = complex queries ), on “incomplete, massive” KG?

Types of Queries

(a) One-Hop queries

(b) Path queries

(c) Conjunctive queries

(a) Predictive one-hop queries

KG completion \(\approx\) one-hop queries

• KG completion : is link \((h,r,t)\) in KG?
• One-hop query : is \(t\) the answer to query \((h,r)\) ?

(b) Path queries

• generalization of one-hop queries
• add more relations on the path
• ex) \(n\)-hop path query :
  • \(q = (v_a, (r_1, \cdots r_n))\).
  • \(v_a\) : anchor entity
  • answer = \([[q]]_G\)

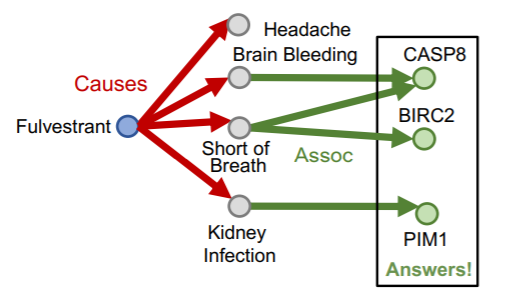
Example : “What proteins are associated with adverse events caused by Fulvestrant?”

• ( anchor entity )
  • \(v_a\) = e : Fulvestrant
• ( relation )
  • \((r_1, r_2)\) = (r : Cause, r : Associate)
• ( query )
  • ( e: Fulvestrant, ( r : Cause, r : Associate ) )

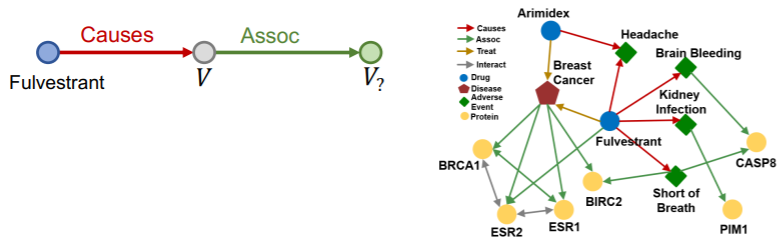
How to answer? traverse in the KG…!?

Problem : KGs are INCOMPLETE! ( = many relations are missing! )

Then, how about…

• (step 1) KG completion
• (step 2) traverse..?

\(\rightarrow\) NO! completed KG is a “dense graph” ( time complexity problem )

Solution : Predictive Queries

\(\rightarrow\) Implicitly impute and account for the incomplete KG

• can answer without KG completion!
• generalization of “link prediction”

11-2. Answering Predictive Queries on KGs

Key idea : Embed queries

• generalize TransE to “multi-hop” reasoning
• ( TransE ) score function : \(f_{r}(h, t)=- \mid \mid \mathbf{h}+\mathbf{r}-\mathbf{t} \mid \mid\)
• ( TransE ) Reinterpretation
  • query embedding : \(\mathbf{q}=\mathbf{h}+\mathbf{r}\)
  • (before) \(f_{r}(h, t)=- \mid \mid \mathbf{h}+\mathbf{r}-\mathbf{t} \mid \mid\)
  • (after) \(f_{q}(t)=- \mid \mid \mathbf{q}-\mathbf{t} \mid \mid\)

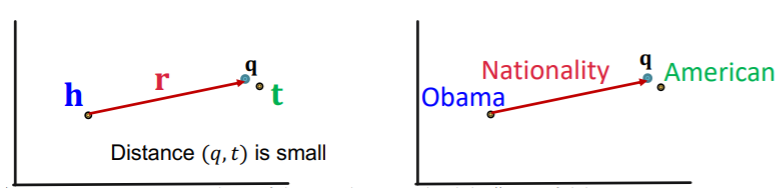
• Query Embedding : just “vector addition”

Example :

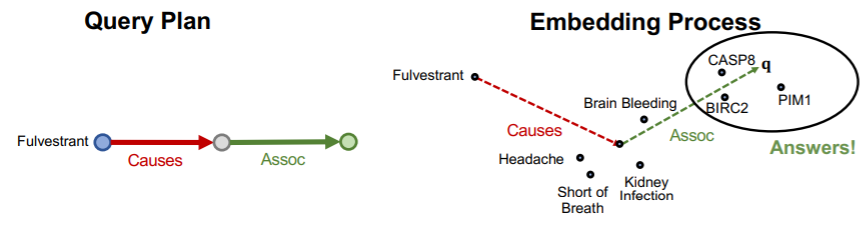
Traversing KG in vector space

• TransE : can handle composition relations
• TransR, DistMult, ComlEx : cannot ~

Conjunctive Queries

how about queries with “logic conjunction” operation?

• ex) “What are drugs that cause Short of Breath AND treat diseases associated with protein ESR2?”

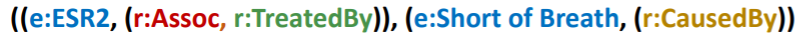
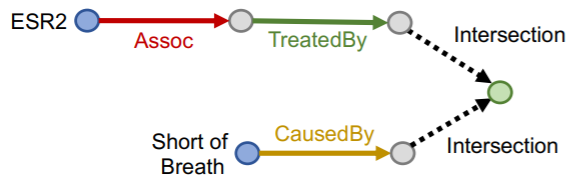
Traverse KG from “2 anchor nodes”

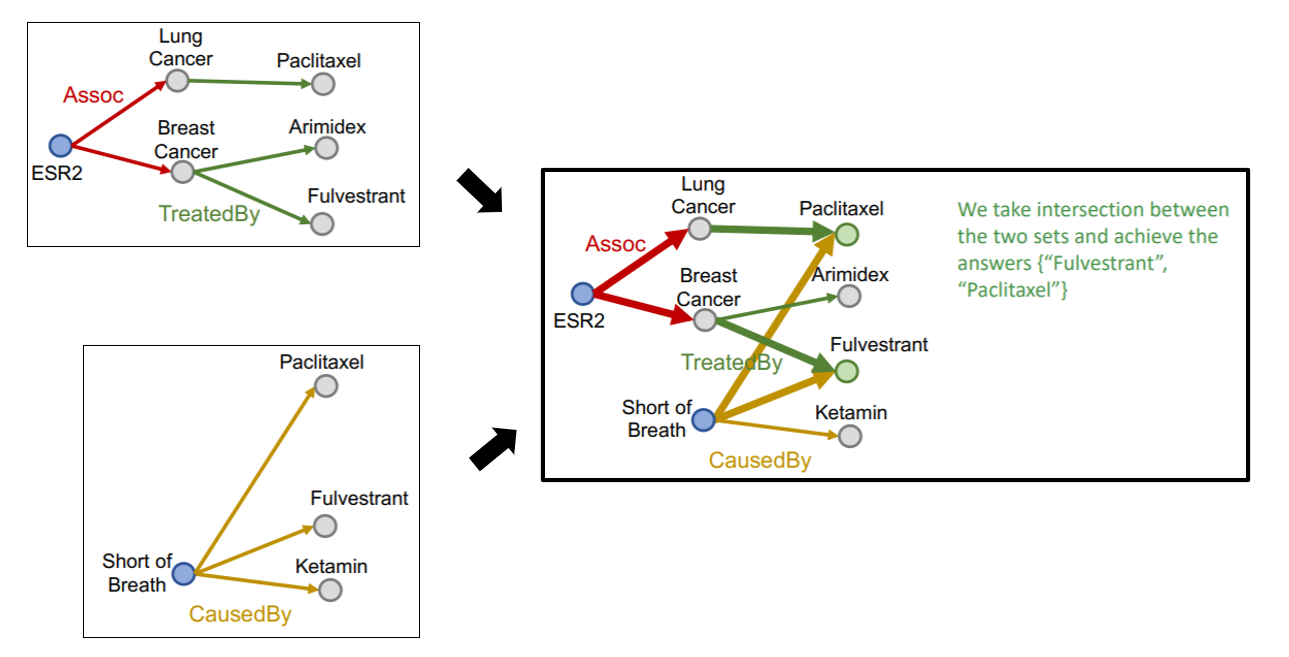
Problem : what is certain link is missing…?

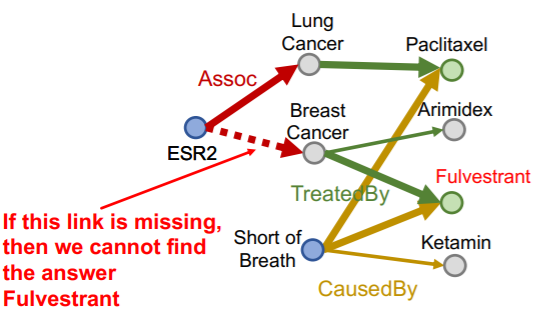
\(\rightarrow\) we have to “implicitly” impute it!

Key point :

• 1) How to make “intermediate node representation”?
• 2) How to define “intersection operation” in latent space?

11-3. Query2Box

Box Embeddings

embed queries with “BOXES”

• \(\mathbf{q}=(\operatorname{Center}(q), \text{Offset}(q))\).
• why? can easily define “intersection of boxes”

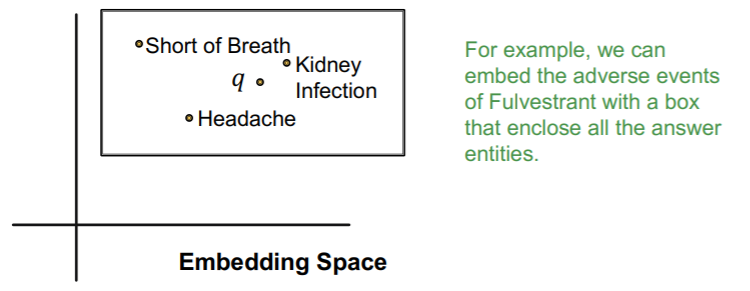
Need to figure out…

• 1) Entity embeddings ( # of params : \(d \mid V \mid\) )
• 2) Relation embeddings ( # of params : \(2 \mid R \mid\) )
• 3) Intersection operator \(f\)

Projection Operator, \(\mathcal{P}\)

• input : box
• projection & expansion : with Relation embedding
• output : box

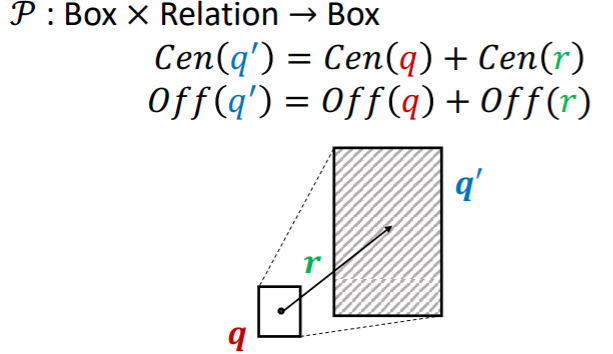
Example :

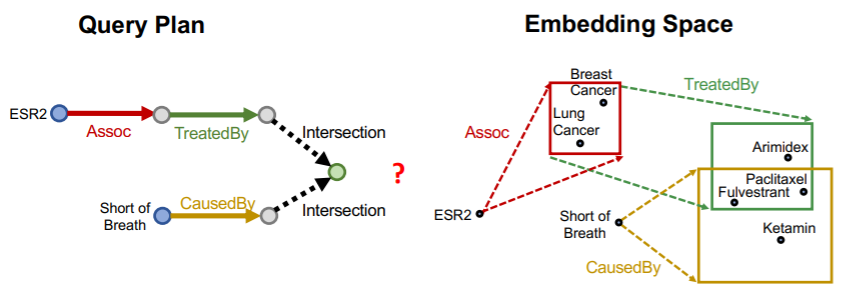
Intersection Operator, \(\mathcal{J}\)

• input : multiple boxes
• output : intersection box
• key point
  • center of new box : weighted average of boxes
  • size of new box : shrink

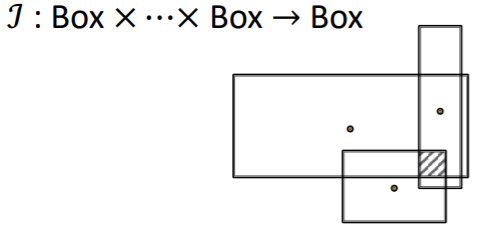
[ a) Center ]

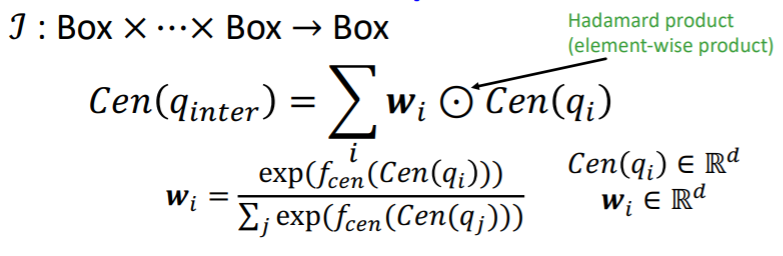
• \(w_i\) : “self-attention” score for each center of each input
• \(f_\text{cen}\) : NN

[ b) Offset ]

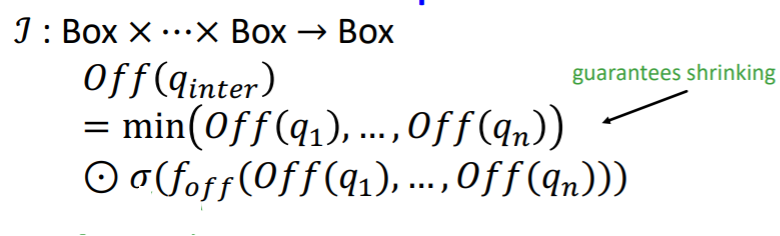
• \(\sigma\) : sigmoid ( 0 ~ 1 )
• \(f_\text{off}\) : NN

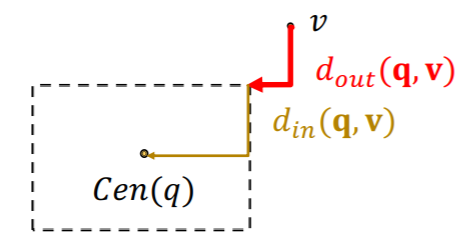
Entity-to-Box distance

Score function \(f_q(v)\) ( = negative distance )

• inverse distance of “node \(v\)” as answer to \(q\)
• notation
  • \(\mathbf{q}\) : query box
  • \(\mathbf{v}\) : entity embedding ( box )
• \(f_q(v) = -d_{\text {box }}(\mathbf{q}, \mathbf{v})\).
• \(d_{\text {box }}(\mathbf{q}, \mathbf{v})=d_{\text {out }}(\mathbf{q}, \mathbf{v})+\alpha \cdot d_{\text {in }}(\mathbf{q}, \mathbf{v})\),
  • where \(0<\alpha<1\).
  • if “inside the box”, “distance should be DOWNweighted”

Union Operation (OR)

• EPFO (Existential Positive First-Order) queries

  = conjunctive queries + disjunction

  = AND-OR queries

• union over arbitrary queries \(\rightarrow\) TOO high dim

  then…how to handle them?

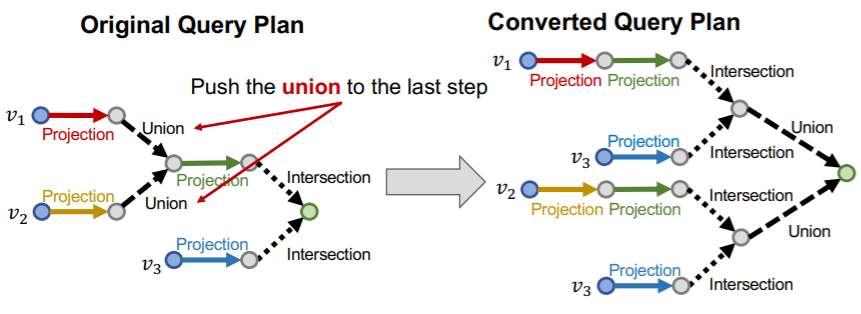
Key idea :

• step 1) take all unions out
• step 2) do union only at the LAST STEP

\(\rightarrow\) Disjunctive Normal Form (DNF)

Disjunctive Normal Form (DNF)

\(q=q_{1} \vee q_{2} \vee \cdots \vee q_{m}\).

• \(q_i\) : conjunctive query

Process

• step 1) embed all \(q_i\)

• step 2) “aggregate at LAST step”

Distance between

• 1) entity embedding \(\mathbf{v}\)
• 2) DNF \(\mathbf{q}\)

\(\rightarrow\) \(d_{b o x}(\mathbf{q}, \mathbf{v})=\min \left(d_{b o x}\left(\mathbf{q}_{1}, \mathbf{v}\right), \ldots, d_{b o x}\left(\mathbf{q}_{m}, \mathbf{v}\right)\right)\)

Training Overview

Intuition : given query embedding \(\mathbf{q}\)…

• maximize \(f_q(v)\) for \(v \in [[q]]\)
• minimize \(f_q(v')\) for \(v \notin [[q]]\)

Parameters :

• 1) Entity embeddings ( # of params : \(d \mid V \mid\) )
• 2) Relation embeddings ( # of params : \(2 \mid R \mid\) )
• 3) Intersection operator \(f\)

Training Procedure

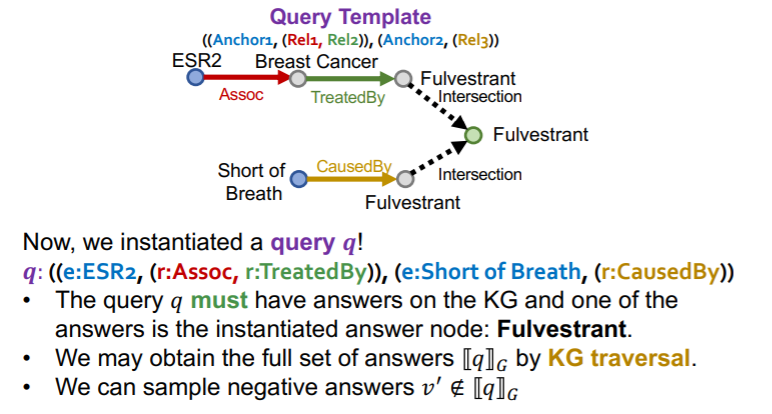
So, how to generate dataset?

( = how to generate queries, from multiple query templates? )

• query templates :

  

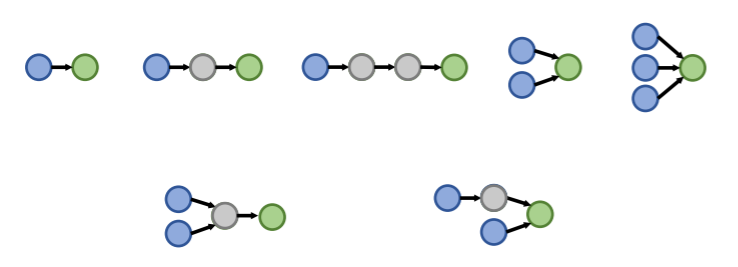
• how to instantiate a query template?

  • Start from instantiating the answer node of the query template, and then iteratively instantiate the other edges and nodes until we ground all the anchor nodes