(CS224W) 12.Frequent Subgraph Mining with GNNs

[ 12. Frequent Subgraph Mining with GNNs ]

( 참고 : CS224W: Machine Learning with Graphs )

Contents

• 12-1. Subgraphs & Motifs

• 12-2. Neural Subgraph Matching
• 12-3. Mining Frequent Subgraphs

1. Subgraphs & Motifs

(1) Introduction

def ) “building blocks” of networks

• can “characterize” & “discriminate” networks

example :

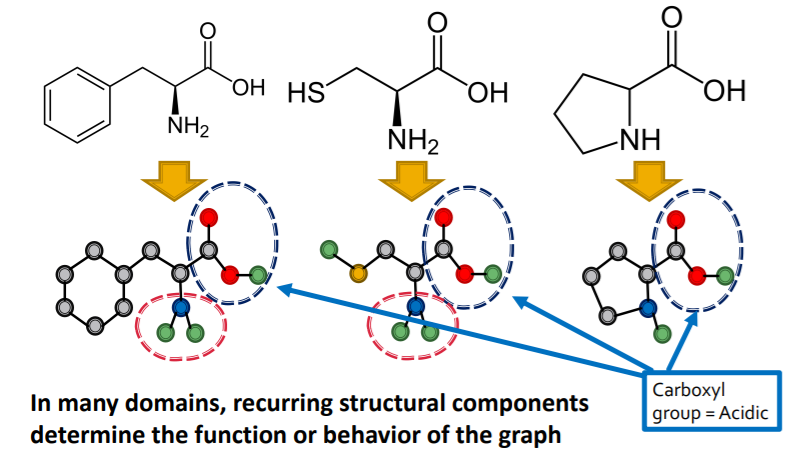
(2) Subgraphs

2 ways to formalize subgraphs

• 1) “NODE”-induced subgraph
• 2) “EDGE”-induced subgraph

a) “NODE”-induced subgraph

• subset of the NODES & all edges induced by the nodes
• called “induced subgraph”
• example )
  • Chemistry ( functional groups )

\[G^{\prime}=\left(V^{\prime}, E^{\prime}\right) \text { is a node induced subgraph iff }\]

• \[V^{\prime} \subseteq V\]
• \[E^{\prime}=\left\{(u, v) \in E \mid u, v \in V^{\prime}\right\}\]
• \[G^{\prime} \text { is the subgraph of } G \text { induced by } V^{\prime}\]

b) “EDGE”-induced subgraph

• subset of the EDGES & all corresponding nodes
• called “non-induced subgraph” / “subgraph”
• example )
  • Knowledge graphs (focus on edges representing logical relations)

\(G^{\prime}=\left(V^{\prime}, E^{\prime}\right) \text { is an edge induced subgraph iff }\).

• \(E^{\prime} \subseteq E\).
• \(V^{\prime}=\left\{v \in V \mid(v, u) \in E^{\prime} \text { for some } u\right\}\).

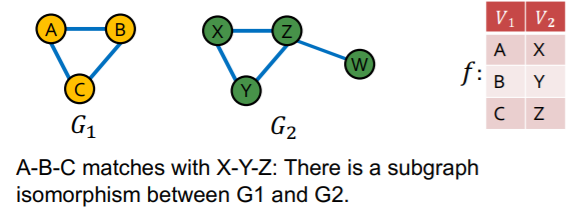
c) Graph Isomorphism

check whether 2 graphs are identical!

[ Definition ]

• \(G_{1}=\left(V_{1}, E_{1}\right)\) and \(G_{2}=\left(V_{2}, E_{2}\right)\) are isomorphic …

  if there exists a bijection \(f: V_{1} \rightarrow V_{2}\) such that \((u, v) \in\) \(E_{1}\) iff \((f(a), f(b)) \in E_{2}\)

  ( + \(f\) is called the isomorphism )

d) Subgraph Isomorphism

[ Definition ]

• \(G_2\) is subgraph isomorphic to \(G_1\) ….

  if some “subgraph of \(G_2\)” is isomorhic to \(G_1\)

  ( = \(G_1\) is a subgraph of \(G_2\) )

\(\rightarrow\) NP-hard problem

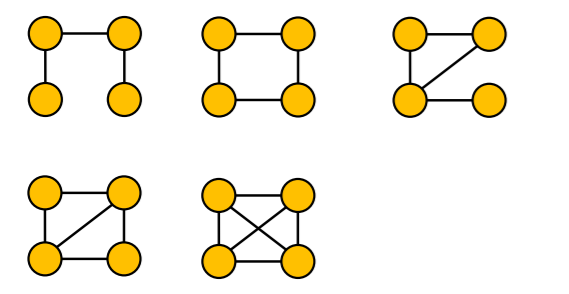
e) Examples

non-isomorphic + connected + undirected + size 4

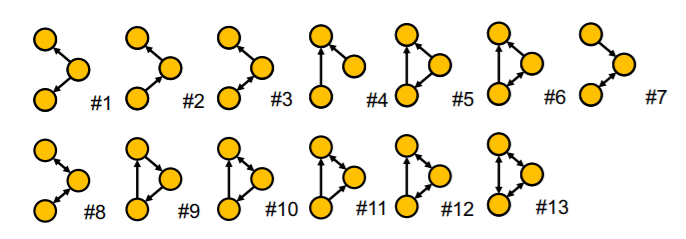
non-isomorphic + connected + directed + size 3

(3) Network Motifs

“(1) recurring, (2) significant (3) patterns of interconnections”

Definition

• (1) Recurring : # of frequency

  \(\rightarrow\) “how to define frequency?”

• (2) Significant : more frequent than random graph

  \(\rightarrow\) “how to define random graph?”

• (3) Pattern : small (node-induced) subgraph

Why do we need motifs?

• Help us understand how graphs work
• Help us make predictions based on presence or lack of presence in a graph dataset

a) Subgraph FREQUENCY (SF)

Notation

• \(G_T\) : Target graph ( = big graph )
• \(G_Q\) : Query graph ( = small graph )

[ Graph-level SF ]

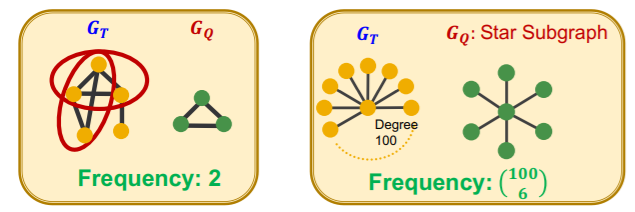
[ Node-level SF ]

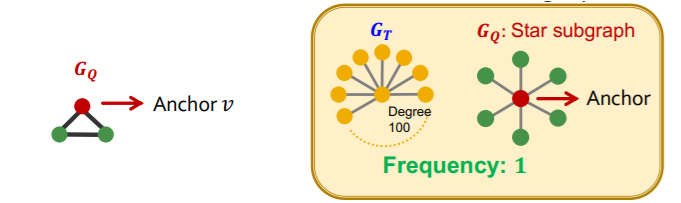
• \((G_Q,v)\) : “node-anchored” subgraph
• robust to outliers

Want to find out “frequency of multiple subgraphs” in dataset!

\(\rightarrow\) treat \(G_T\) as a large dataset, with “disconnected components” ( = individual graphs )

b) Motif SIGNIFICANCE

more frequent than null-model ( = random model )

\(\rightarrow\) so, how to define “RANDOM graphs”?

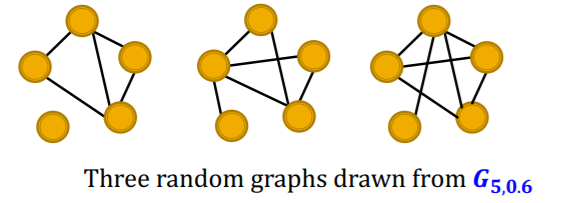
[ Erdos-Renyi (ER) random graphs ]

• \(G_{n,p}\) : undirected graph / \(n\) nodes / edge probability of \(p\)

• can be disconnected

• example :

  

[ Configuration Model ]

• goal : generate random graph…

  • with \(N\) nodes
  • with degree \(k_1, \cdots k_N\)

• compare

  • (1) \(G^{\text{real}}\)
  • (2) \(G^{\text{random}}\)

  ( both have same degree sequence! )

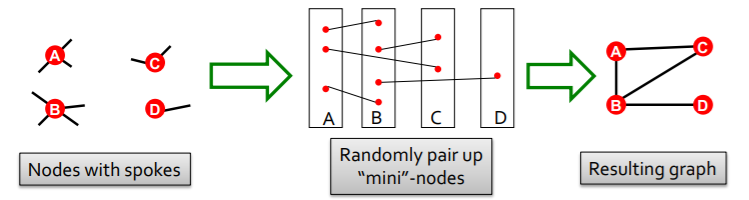
Overview

• intuition : Motifs are overrepresented in a network when compared to random graphs

• 3 step

  • step 1) count motifs in \(G^{\text{real}}\)

  • step 2) generate random graph

    • with similar statistics

      ( ex. nodes / edges / degree sequences)

  • step 3) use statistical measures to evaluate “significance of each motif”

    • ex) Z-score

Z-score :

• \(Z_i\) : captures “significance” of motif \(i\)
• \(Z_{i}=\left(N_{i}^{\mathrm{real}}-\bar{N}_{i}^{\mathrm{rand}}\right) / \operatorname{std}\left(N_{i}^{\mathrm{rand}}\right)\).
  • \(N_{i}^{\text {real }}\) : # (motif \(i\) ) in graph \(G^{\text {real }}\)
  • \(\bar{N}_{i}^{\text {rand }}\) : average #(motifs \(i\) ) in random graph
• Network significance profile (SP) : normalized Score

Network significance profile (SP) :

• \(S P_{i}=Z_{i} / \sqrt{\sum_{j} Z_{j}^{2}}\).
• vector of “normalized Z-scores”
• dimension = # of types of motifs
• meaning : relative significance of subgraphs

2. Neural Subgraph Matching

(1) Subgraph Matching

Question : is QUERY graph a subgraph of TARGET graph?

• QUERY graph : connected
• TARGET graph : can be disconnected

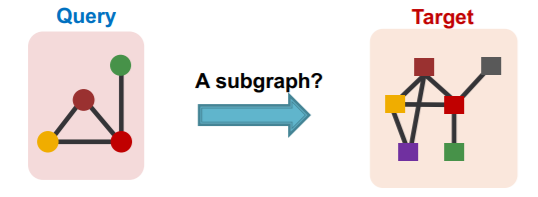
use GNN to “predict” subgraph isomorphism

• binary prediction

• use embeddings to decide if neighborhood of \(u\) is isomorphic to subgraph of neighborhood of \(v\)

• do not only predict its existence,

  but also identify corresponding nodes \(u\) & \(v\)

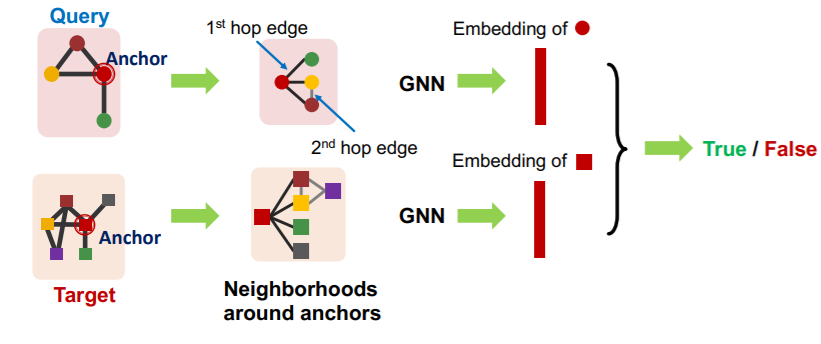
a) Decomposing graphs ( into neighborhoods )

• 1) for each node in \(G_T\) ….
  • obtain a k-hop neighborhood around the anchor
• 2) for each node in \(G_Q\) ….
  • same
• 3) embed all those neighborhoods with GNN
  • By computing the embeddings for the anchor

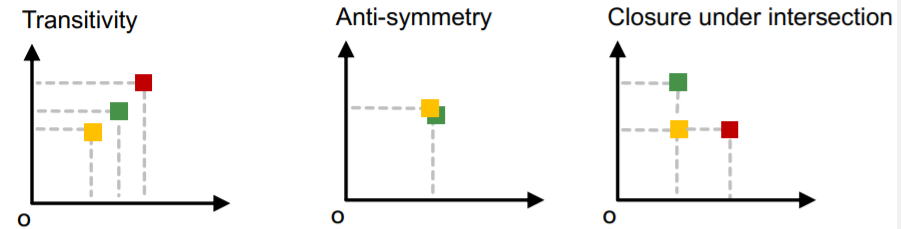
b) Order Embedding Space

• mapping : graph \(A\) \(\rightarrow\) point \(Z_A\)
• \(Z_A\) is non-negative in all dimensions
• key point : Transitivity

• Example

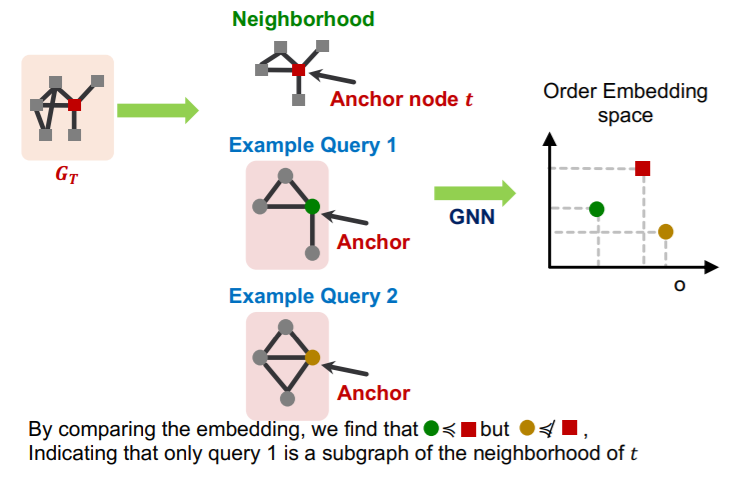
Why “order embedding space”?

• 1) transitivity

  • if \(G_1\) is a subgraph of \(G_2\) and \(G_2\) is a subgraph of \(G_3\)

    \(\rightarrow\) then \(G_1\) is a subgraph of \(G_3\)

• 2) anti-symmetry

  • if \(G_1\) is a subgraph of \(G_2\) and \(G_2\) is a subgraph of \(G_1\)

    \(\rightarrow\) then \(G_1\) is isomorphic to \(G_2\)

• 3) closure under intersection

c) Order constraint

• What loss function should we use, so that the learned order embedding reflects the subgraph relationship?
• design loss functions based on the order constraint

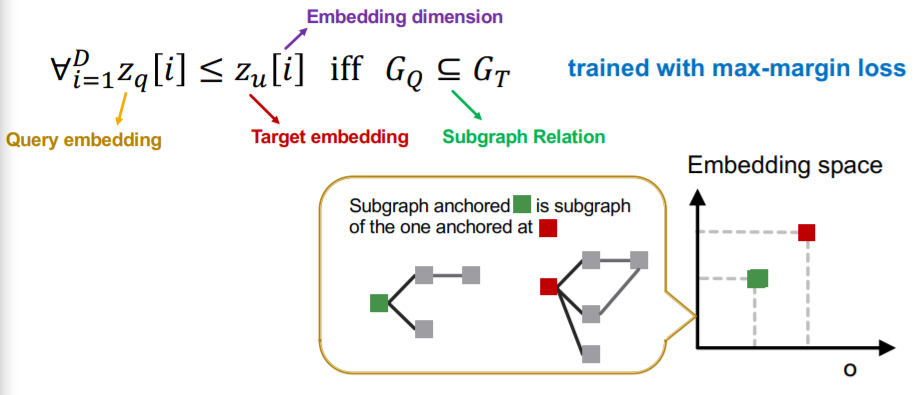
d) Max-margin Loss

• optimize by minimizing “Max-margin loss”

• margin between \(G_q\) & \(G_t\)

  = \(E\left(G_{q}, G_{t}\right)=\sum_{i=1}^{D}\left(\max \left(0, z_{q}[i]-z_{t}[i]\right)\right)^{2}\)

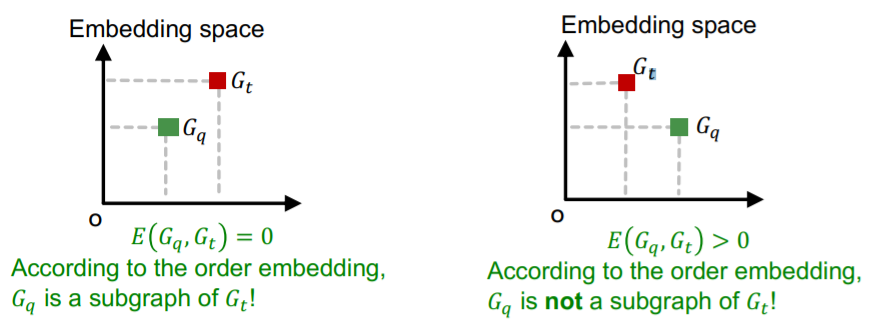
\(E\left(G_{q}, G_{t}\right)=0\), when \(G_{q}\) is a subgraph of \(G_{t}\)

\(E\left(G_{q}, G_{t}\right)>0\), when \(G_{q}\) is not a subgraph of \(G_{t}\)

Trained in a way that…

• 1) positive examples :
  • minimize \(E(G_q, G_t)\), when \(G_q\) is a subgraph of \(G_t\)
• 2) negative examples :
  • minimize \(\text{max}(0,\alpha-E(G_q,G_t))\)

3. Mining Frequent Subgraphs

(1) Representation Learning

Goal : find most frequent size-\(k\) motifs!

Process

• 1) enumerate all size-\(k\) connected subgraphs
• 2) count # of each subgraph types

But computationally hard….

\(\rightarrow\) use “REPRESENTATION learning”

how?

• task 1) Combinatorial explosion

  solution 1) organize the search space

• task 2) Subgraph isomorphism

  solution 2) prediction using GNN

Settings

• \(G_T\) : target graph
• \(k\) : size parameter
• \(r\) : desired number of results ( = TOP \(r\) graphs )

Task

• among all possible graphs of \(k\) nodes,

  identify top \(r\) graphs with highest frequency in \(G_T\)

• use “node-level” definition

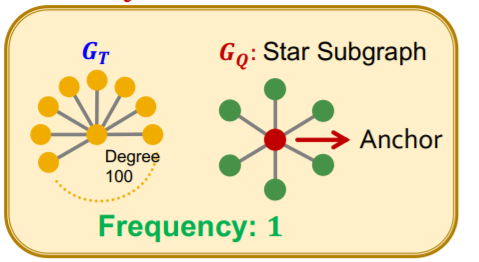
(2) SPMiner

a) overview

• SPMiner = neural model to identify frequent motifs

• procedure

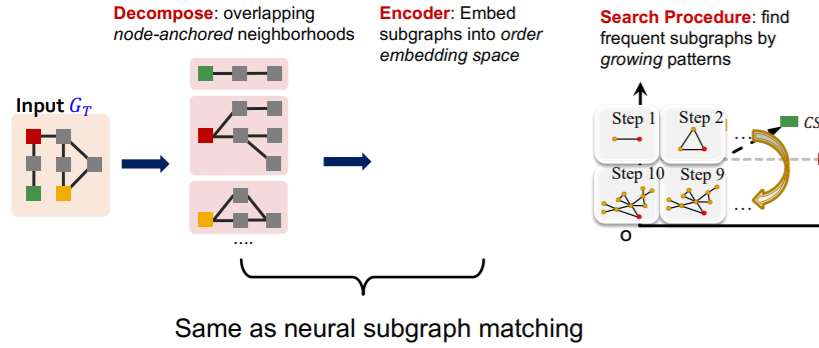
  • step 1) decompose
    • decompose into subgraphs
    • overlapping node-anchored neighborhoods ( ex. 2-hop )
  • step 2) encoder
    • embed subgraphs
    • caution : to “order embedding” space
      • can quickly find out the frequency of a given subgraph \(G_Q\)
  • step 3) search procedure
    • find frequent subgraphs, by “growing patterns”

  

b) Motif Frequency Estimation with SPMiner

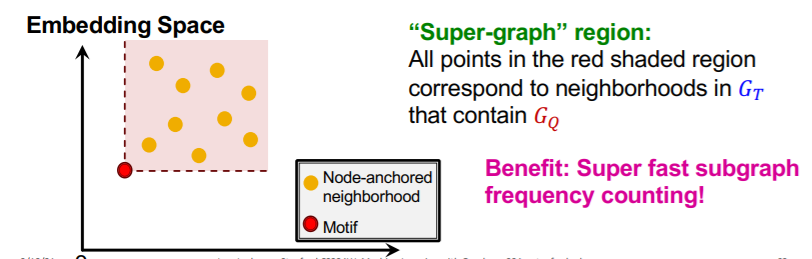
\(G_{N_i}\) = set of subgraphs of \(G_T\)

Task :

• estimate frequency of \(G_Q\) ( = query graph = motif = red dot )
• by counting the number of \(G_{N_i}\) ( = yellow dot )
• such that their embeddings \(Z_{N_i}\) satisfy \(Z_Q \leq Z_{N_i}\)

[ Search Procedure ]

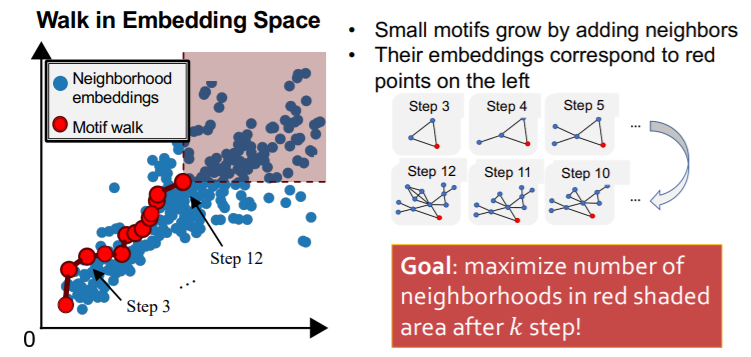
• step 1) randomly select starting node \(u\) in \(G_T\)
  • set \(S=\{u\}\)
• step 2) Grow a motif iteratively…
  • choose a neighbor of node in \(S\) & add it to \(S\)
  • grow motifs to find larger motifs
• step 3) Terminate
  • when reached a desired motif size
  • tesult : “subgraph of target graph induced by \(S\)”

[ Choosing the next node ]

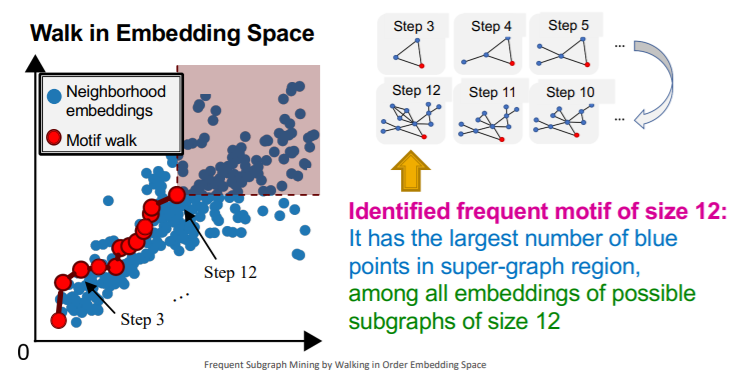
• Total Violation of a subgraph \(G\)

  = # of neighborhoods, that do not contain \(G\)

  = # of neighborhoods, that do not satisfy \(Z_Q \leq Z_{N_i}\)

• minimizing Total Violation

  = maximizing frequency

• use “GREEDY strategy”

  • at every step, add node that gives “smallest total violation”