[ 13. Community Detection in Networks ]
( 참고 : CS224W: Machine Learning with Graphs )
Contents
- 13-1. Community Detection in Networks
- 13-2. Network Communities
- 13-3. Louvain Algorithm
- 13-4. Detecting Overlapping Communities : BigCLAM
1. Community Detection in Networks
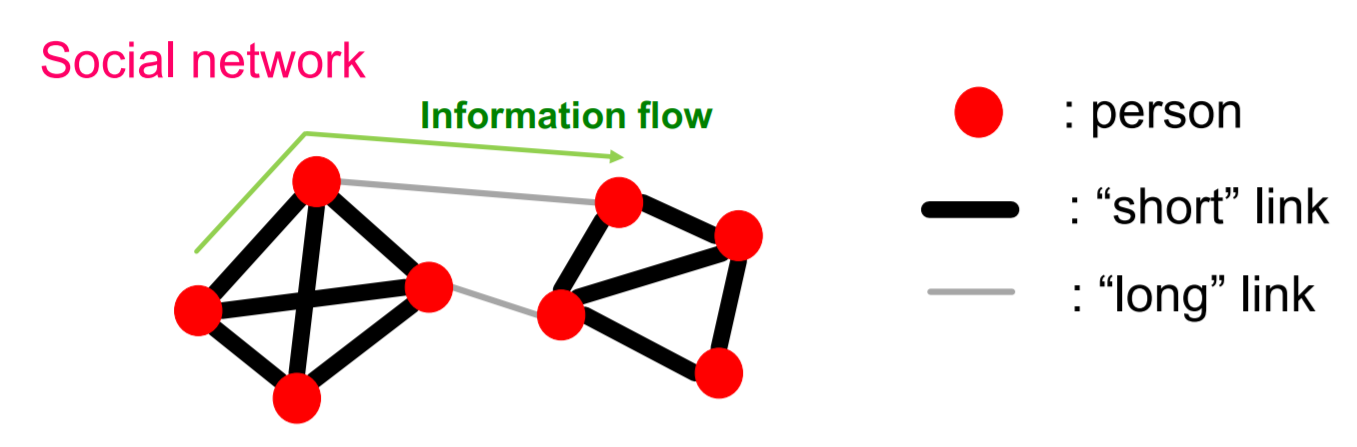
(1) Flow of Information
- people are “embedded” in social network
- Information flows through links
- 1) short link
- 2) long link
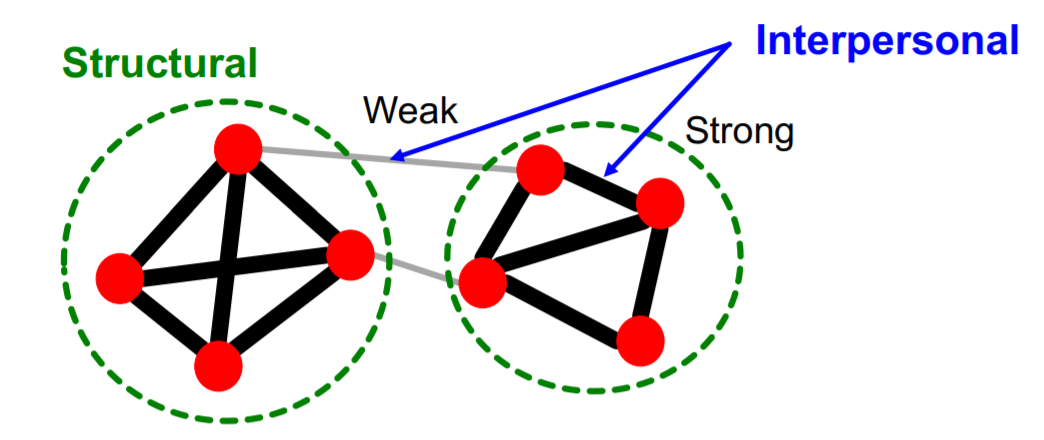
(2) Two perspective of friendships
1) Structural
- span different parts of the network
- ex) group (A), group (B), ..
2) Interpersonal
- friendship between person (a) & person (b)
- ex) strong, weak
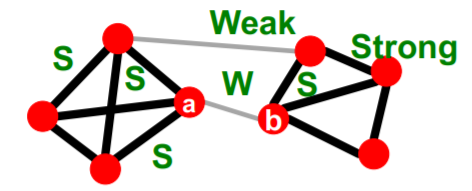
(3) Granovetter’s Explanation
connection between the (1) social and (2) structural role of an edge
1) Structure
- Structurally embedded (tightly-connected) edges = socially STRONG
- Long-range edges = socially WEAK
2) Information
- Structurally embedded (tightly-connected) edges = heavily REDUNDANT
- Long-range edges = allows to gather new INFORMATION
(4) Triadic Closure
key idea : if (A&B) and (B&C) \(\rightarrow\) (A&C) is likely!
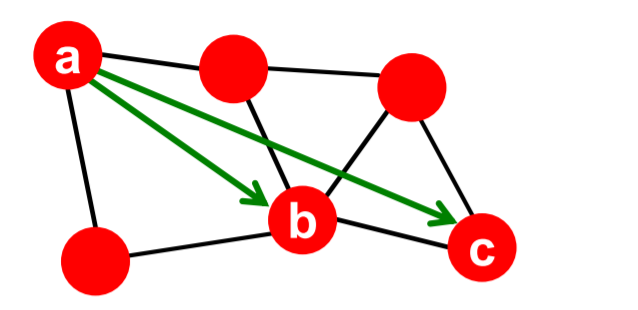
Triadic closure = High clustering coefficient
[ Intuition ]
if B and C both have “friend A” in common…
- 1) B is more likely to meet C
- 2) B & C trust each other
- 3) A has incentive to bring B & C together
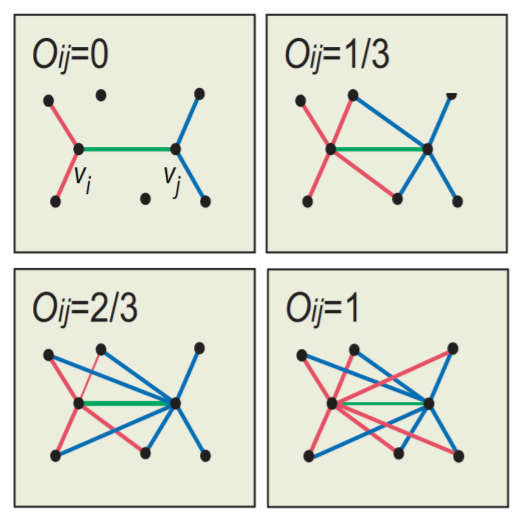
(5) Edge Overlap
\(O_{i j}=\frac{ \mid (N(i) \cap N(j))-\{i, j\} \mid }{ \mid (N(i) \cup N(j))-\{i, j\} \mid }\).
- \(N(i)\) : neighbors of node \(i\)
(6) Conceptual Picture of Networks
2. Network Communities
(1) Granovetter’s theory
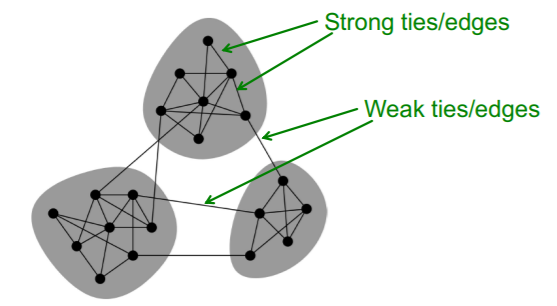
Networks = composed of “tightly connected set of nodes”
Network Communities
- lots of internal connections
- few external connections
\(\rightarrow\) so, how to “automatically find densely connected groups”?
(2) Social Network Data
Examples
- Zachary’s Karate Club network
- Micro-Markets in Sponsored Search
- NCAA Football network
(3) Modularity \(Q\)
Modularity = measure of “how well a network is PARTITIONED” into communities
- small communities ( disjoint networks ) : \(s \in S\)

Null model = “Configuration Model”
- settings :
- graph : \(G\)
- # of nodes : \(n\)
- # of edges : \(m\)
- construct rewired network \(G^{'}\)
Expected number of edges between nodes \(i\) & \(j\) ( of degrees \(k_i\) & \(k_j\) )
= \(k_{i} \cdot \frac{k_{j}}{2 m}=\frac{k_{i} k_{j}}{2 m}\).
- \(2m\) : # of directed edges
Expected number of edges in (multigraph) \(G^{'}\) :
\(\begin{aligned} &=\frac{1}{2} \sum_{i \in N} \sum_{j \in N} \frac{k_{i} k_{j}}{2 m}=\frac{1}{2} \cdot \frac{1}{2 m} \sum_{i \in N} k_{i}\left(\sum_{j \in N} k_{j}\right)= \\ &=\frac{1}{4 m} 2 m \cdot 2 m=m \end{aligned}\).
Modularity of partitioning \(S\) of graph \(G\)
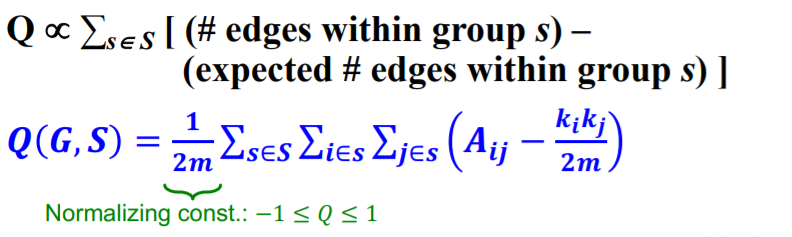
- range : [ -1 ~ 1 ]
- if positive, number of edges within group exceeds the expected number
-
greater than 0.3~0.7 : significant community structure
- both applicable to “weighted & unweighted” networks
Reformulation :


3. Louvain Algorithm
(1) Introduction
- “Greedy” algorithm
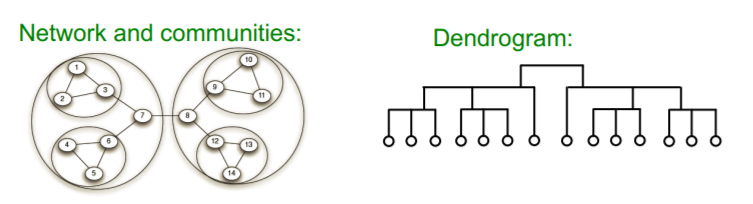
- work both for “weighted & unweighted” graphs
- provides “Hierarchical” communities
- details
- fast
- rapid convergance
- high modularity output
(2) 2 Phases
[ Phase 1 ] Modularity is optimized by allowing only local changes to node-communities memberships
[ Phase 2 ] The identified communities are aggregated into super-nodes to build a new network
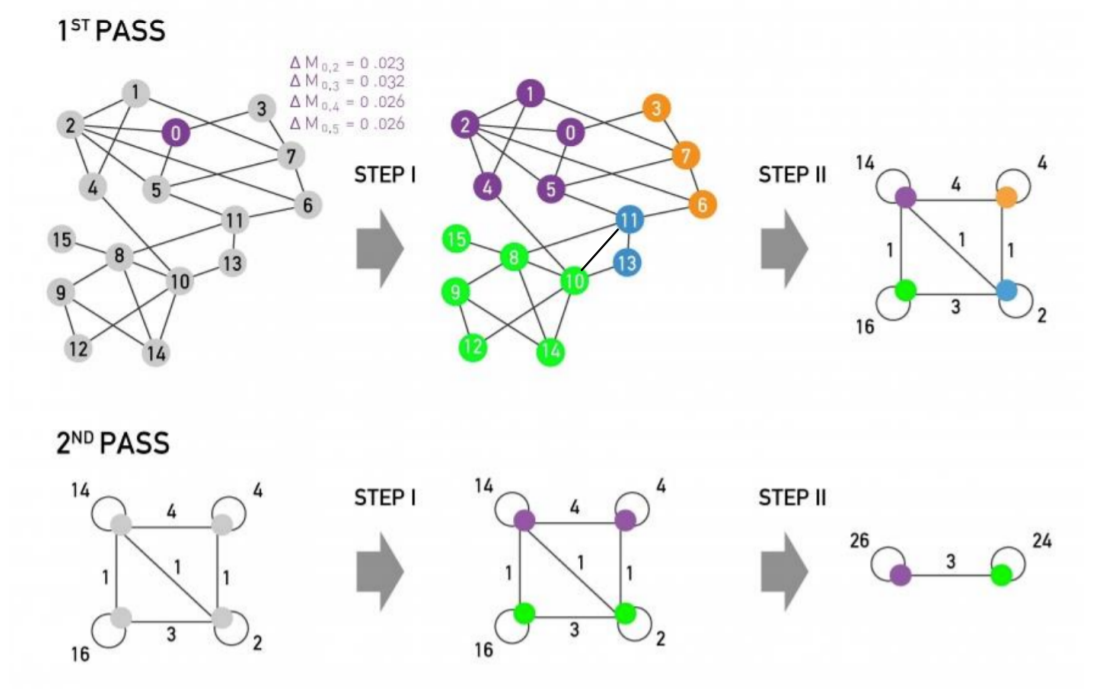
Phase 1
- step 1) set each node as “distinct community”
- step 2) for ( \(i\) in ALL_NODES ) :
- compute \(\Delta Q\) , when putting node \(i\) into “community of neighbor \(j\)”
- change the community of \(i\) to node \(j\), which gives the largest gain in \(\Delta Q\)
- run until no movement
Modularity Gain, \(\Delta Q\)
settings : “move node \(i\) from community \(D\) to \(C\) “
- \(\Delta Q(D \rightarrow i \rightarrow C)=\Delta Q(D \rightarrow i)+\Delta Q(i \rightarrow C)\).
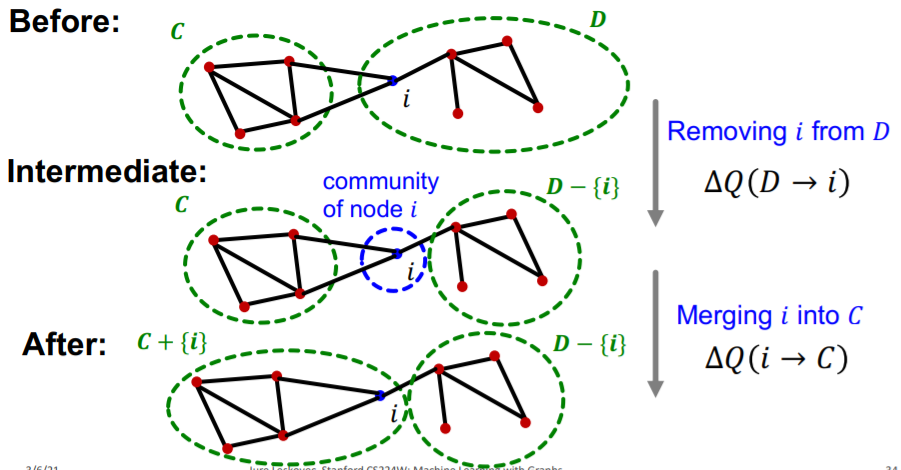
How to calculate \(\Delta Q(i \rightarrow C)\) ?
-
step 1) calculate \(Q(C)\) ( = modularity within \(C\) )
- Notation
- \(\boldsymbol{\Sigma}_{\boldsymbol{i n}} \equiv \sum_{i, j \in C} A_{i j}\) : ~ link “BETWEEN” nodes in \(C\)
- \(\boldsymbol{\Sigma}_{\boldsymbol{t o t}} \equiv \sum_{i \in C} k_{i}\) : ~ link “ALL” nodes in \(C\)
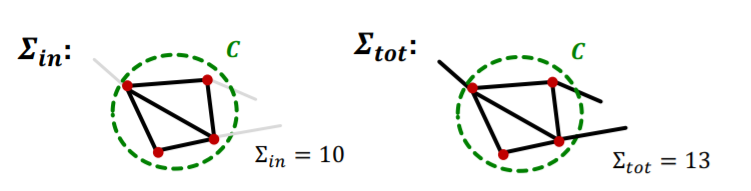
- Notation
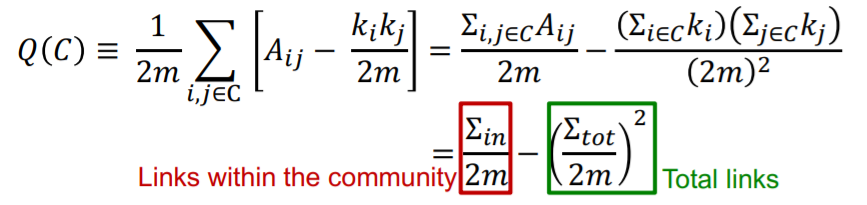
-
step 2) calculate \(k_{i,in}\) & \(k_{i}\)
-
Notation
- \(\boldsymbol{k}_{\boldsymbol{i}, \boldsymbol{i n}} \equiv \sum_{j \in C} A_{i j}+\sum_{j \in C} A_{j i}\) : sum of link BETWEEN node \(i\) & \(C\)
- \(\boldsymbol{k}_i\) : sum of ALL link of node \(i\)
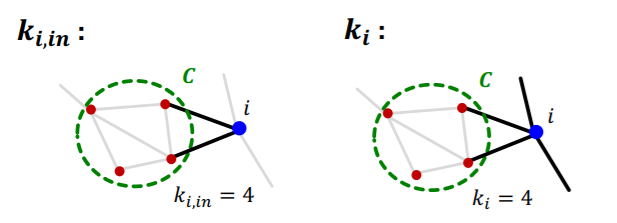
-
- step 3) calculate \(Q_{before}\) & \(Q_{after}\)
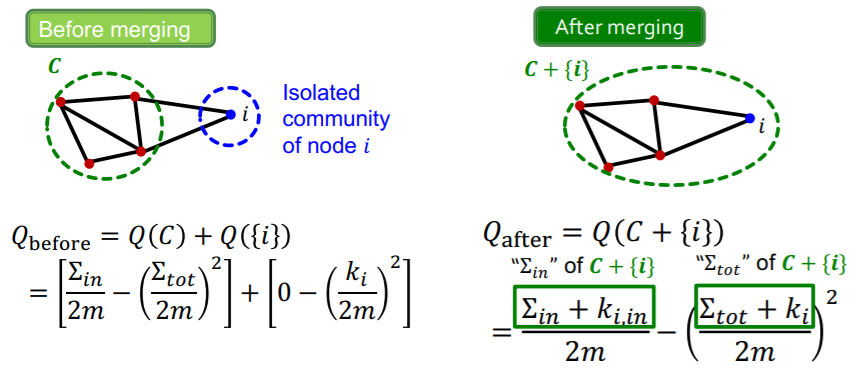
-
step 4) calculate \(\Delta Q(i \rightarrow C)\)
\(\Delta Q(i \rightarrow C)= Q_{\text {after }}-Q_{\text {before }} \\ =\left[\frac{\Sigma_{i n}+k_{i, i n}}{2 m}-\left(\frac{\Sigma_{t o t}+k_{i}}{2 m}\right)^{2}\right] -\left[\frac{\Sigma_{i n}}{2 m}-\left(\frac{\Sigma_{t o t}}{2 m}\right)^{2}-\left(\frac{k_{i}}{2 m}\right)^{2}\right]\).
( calculate \(\Delta Q(D \rightarrow i)\) in the same way )
(3) Summary
[ Phase 1 ]
- calculate \(C^{\prime}=\operatorname{argmax}_{\mathrm{C}}, \Delta Q\left(C \rightarrow i \rightarrow C^{\prime}\right)\)
- if \(\Delta Q\left(C \rightarrow i \rightarrow C^{\prime}\right)>0\), then update
- \(C \leftarrow C-\{i\}\).
- \(C^{\prime} \leftarrow C^{\prime}+\{i\}\).
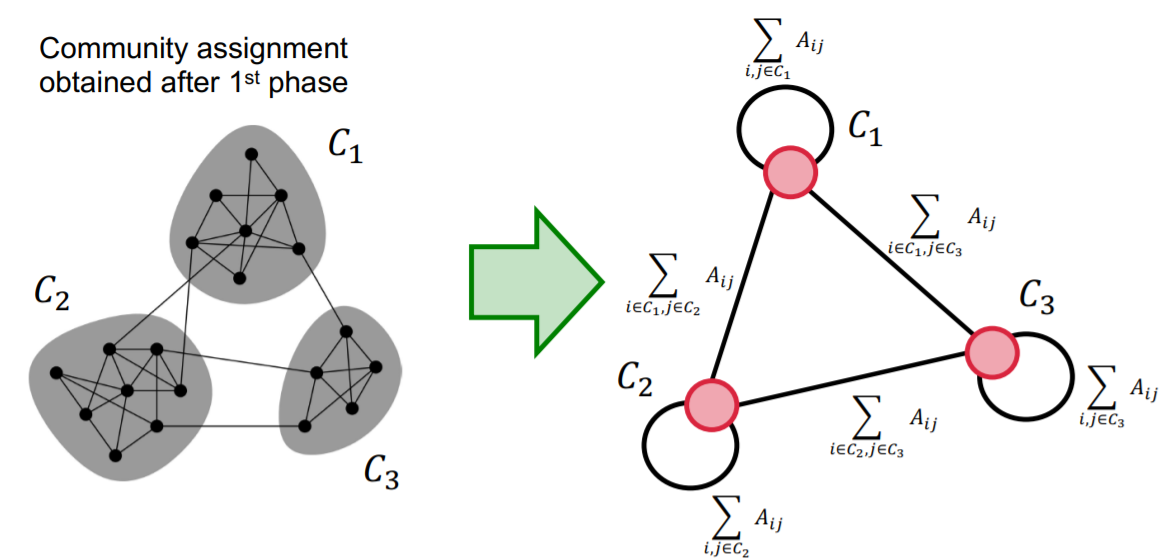
[ Phase 2 ]
- communities obtained in the first phase are contracted into super-nodes
- then, do the same as [ Phase 1 ] on the super-node network
4. Detecting Overlapping Communities : BigCLAM
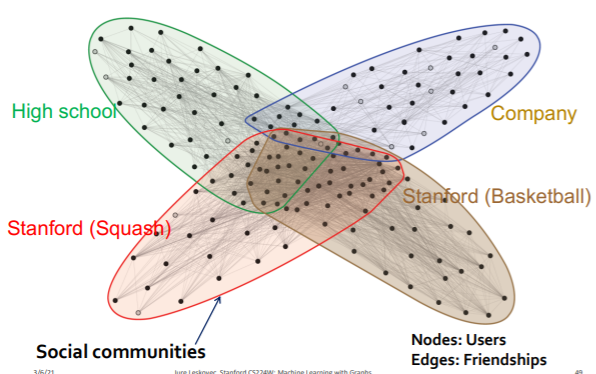
(1) Overlapping Communities
(2) Plan of Action
step 1) Community Affiliation Graph Model (AGM)
- define a “GENERATIVE” model for graphs
- based on “node community affiliations”
step 2) for a given graph \(G\)…
- assume \(G\) was generated by AGM
- find the best AGM
(3) Community AGM
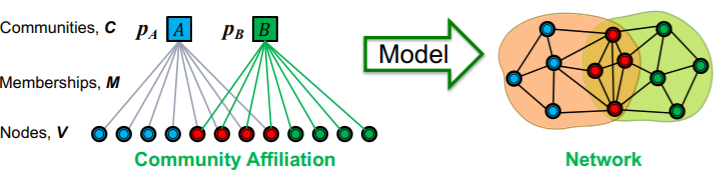
Model parameters
- node \(V\), community \(C\), membership \(M\)
- each community has a single probability \(p_c\)
Can express a variety of community structures
- ex) non-overlapping, overlapping, nested
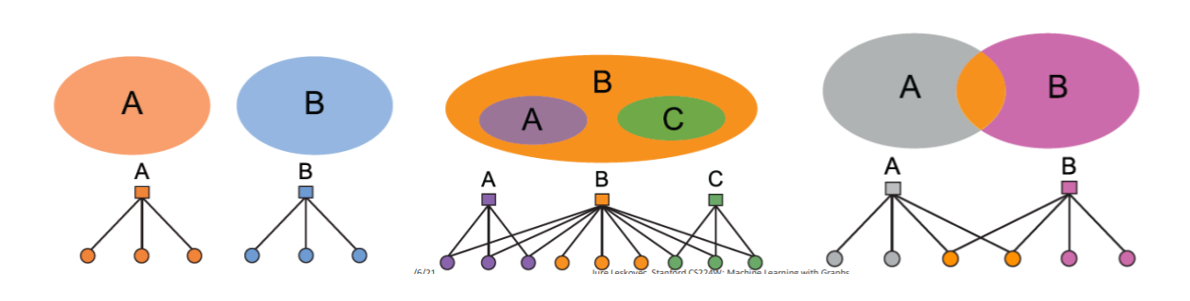
generative process
- \(p_c\) : nodes in community \(c\), connect to each other by probability \(p_c\)
- \(p(u, v)=1-\prod_{c \in M_{u} \cap M_{v}}\left(1-p_{c}\right)\),
- since multiple communities!
(4) Detecting Communities
how to detect communities with AGM?
\(\rightarrow\) given a GRAPH, find a MODEL \(F\)
- optimize using MLE

- efficiently calculate \(P(G\mid F)\)
Graph Likelihood , \(P(G\mid F)\)
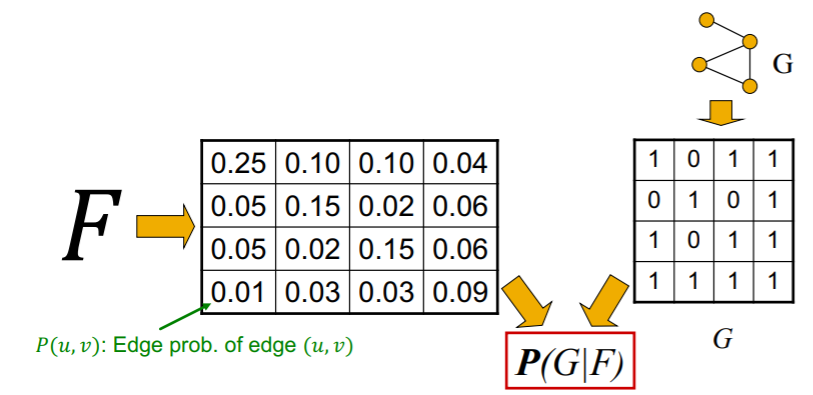
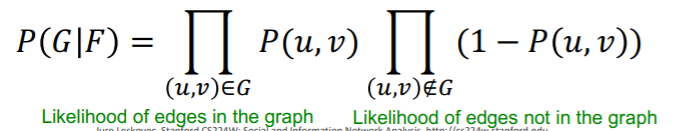
Strengths of membership
\(F_{uA}\) : membership strength, of node \(u\) to community \(A\)
- \(F_{uA}=0\) : NO membership
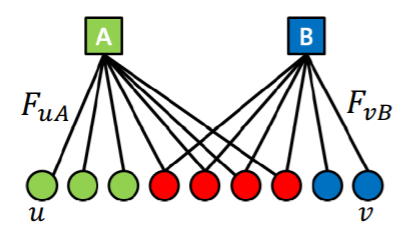
\(P_C(u,v)\) : probability \(u\) &\(v\) are connected (for community \(C\))
- \(P_{C}(u, v)=1-\exp \left(-F_{u C} \cdot F_{v C}\right)\).
- \(F_{uC}\) & \(F_{vC}\) : non-negative
- valid probability : [ 0 ~ 1 ]
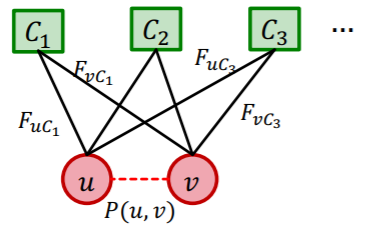
\(P(u,v)\) : probability \(u\) &\(v\) are connected (for at least one communities)
-
\(P(u, v)=1-\prod_{C \in \Gamma}\left(1-P_{C}(u, v)\right)\).
-
expand..
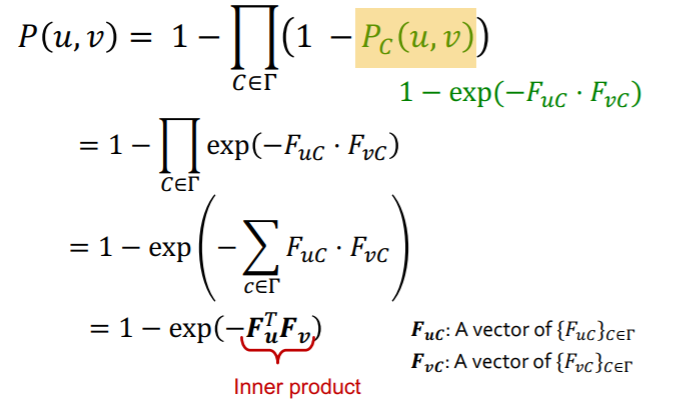
(5) BigCLAM
Key idea :
-
Probability of nodes \(u\) & \(v\) linking
= proportional to the strength of shared memberships
( \(\mathbf{P}(\boldsymbol{u}, \boldsymbol{v})=\mathbf{1}-\boldsymbol{\text { exp }}\left(-\boldsymbol{F}_{\boldsymbol{u}}^{\boldsymbol{T}} \boldsymbol{F}_{v}\right)\) )
-
given \(G(V, E)\), maximize likelihood of \(G\) , under \(F\)
Likelihood
\(\begin{aligned} P(G \mid F) &=\prod_{(u, v) \in E} P(u, v) \prod_{(u, v) \notin E}(1-P(u, v)) \\ &=\prod_{(u, v) \in E}\left(1-\exp \left(-F_{u}^{T} F_{v}\right)\right) \prod_{(u, v) \notin E} \exp \left(-F_{u}^{T} F_{v}\right) \end{aligned}\).
Log Likelihood
\(\begin{aligned} &\log (P(G \mid \boldsymbol{F})) \\ &=\log \left(\prod_{(u, v) \in E}\left(1-\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right) \prod_{(u, v) \notin E} \exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right) \\ &=\sum_{(u, v) \in E} \log \left(1-\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right)-\sum_{(u, v) \notin E} \boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v} \\ &\equiv \ell(\boldsymbol{F}): \text { Our objective } \end{aligned}\).
Optimization
-
goal : optimize \(\ell(\boldsymbol{F})\)
-
start with random \(F\)
-
iterate until convergence
- “gradient ascent”
- partial derivative :
- \(\nabla \ell(\boldsymbol{F})=\sum_{v \in \mathcal{N}(u)}\left(\frac{\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)}{1-\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)}\right) \cdot \boldsymbol{F}_{v}-\sum_{v \notin \mathcal{N}(u)} \boldsymbol{F}_{v}\).
-
solution for Time Complexity :
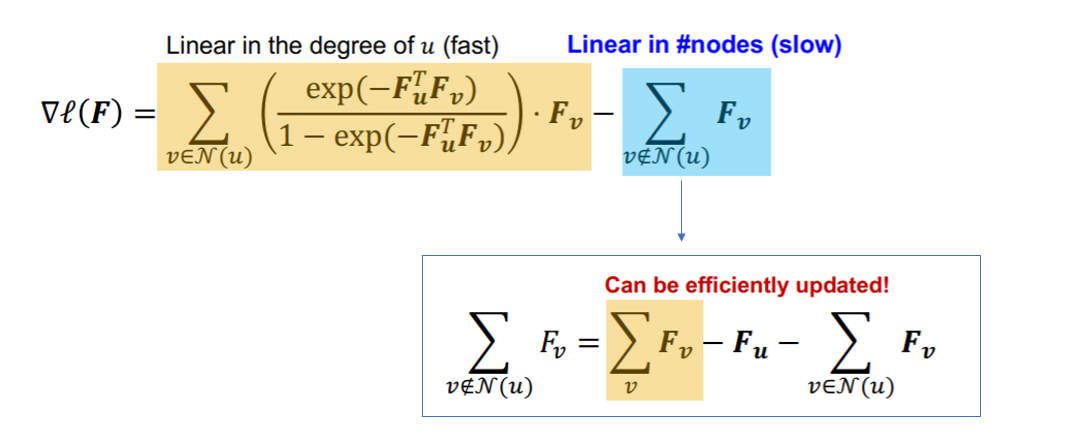
- \(\sum_{v} \boldsymbol{F}_{v}\) : can be computed at the beginning!
