(CS224W) 6.Graph Neural Networks

[ 6. Graph Neural Networks ]

( 참고 : CS224W: Machine Learning with Graphs )

Contents

• 6-1. Introduction
• 6-2. DL for graphs
• 6-3. GCN (Graph Convolution Networks)
• 6-4. GNN vs CNN
• 6-5. GNN vs Transformer

6-1. Introduction

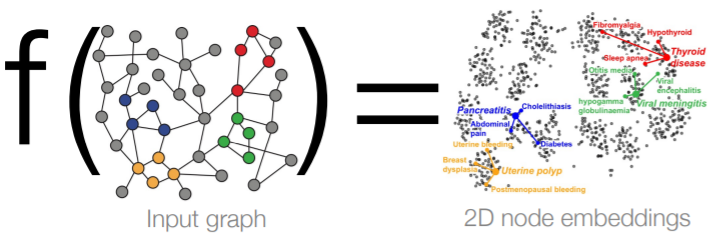
learn mapping function via NN!

• similar nodes, close in embedding space

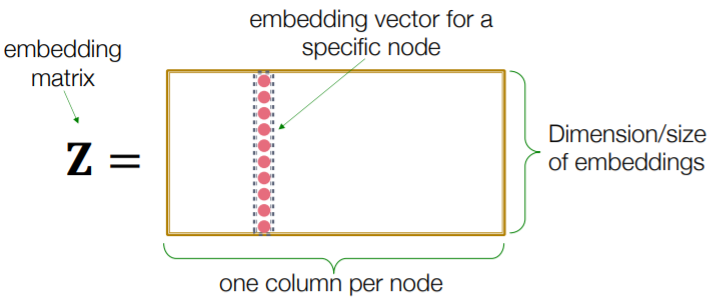
Shallow Encoders

• just “embedding-lookup table”
• limitations :
  • 1) \(O(\mid V \mid)\) parameters needed
  • 2) “transductive”
    • no embeddings for unseen nodes
  • 3) do not use “node features”

Networks are complex!

• arbitrary size & complex topological structure
• no fixed node ordering / reference point
• dynamic & multimodal features

6-2. DL for graphs

Notation

• \(V\) : vertex set
• \(A\) : adjacency matrix
• \(\boldsymbol{X} \in \mathbb{R}^{m \times \mid V \mid}\) : matrix of “node features”
• \(N(v)\) : neighbors of node \(v\)

Naive approach : use concat ( [\(A\) , \(X\)] ) as input

CNN : problems?

• no fixed notion of locality or sliding window on the graph

  ( there can be many order plans :( )

(1) Permutation invariant function

• input graph : \(G=(\boldsymbol{A}, \boldsymbol{X})\)

• map \(G\) into vector \(\mathbb{R}^{d}\)

• \(f\) is “Permutation invariant function”,

  if \(f\left(\boldsymbol{A}_{i}, \boldsymbol{X}_{i}\right)=f\left(\boldsymbol{A}_{j}, \boldsymbol{X}_{j}\right)\) for any order plan \(i\) &\(j\)

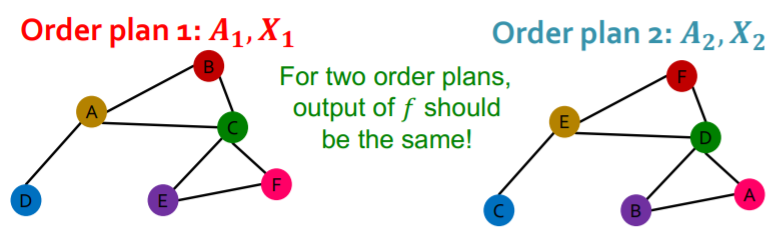
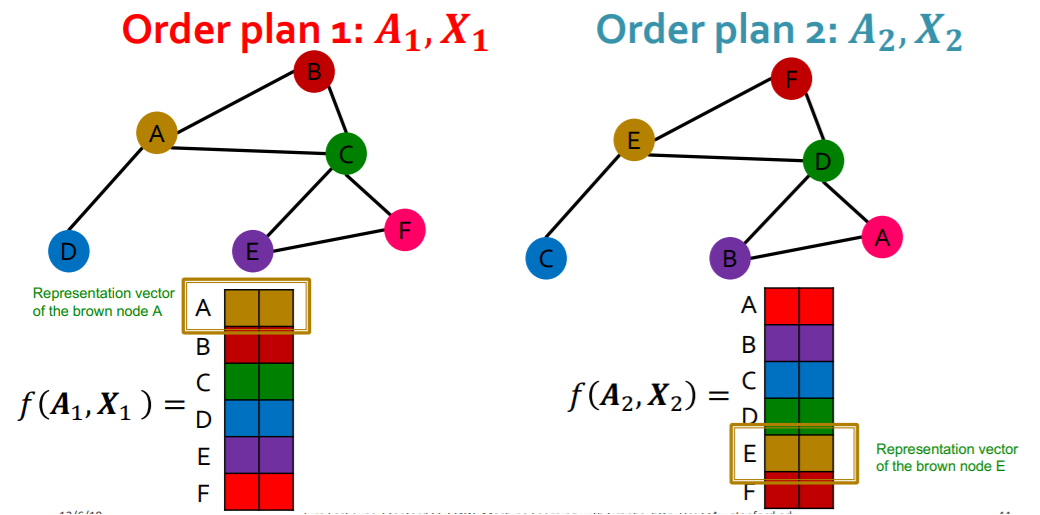
(2) Permutation Equivariance

for 2 order plans..

the vector of “SAME POSITION” should have “SAME EMBEDDING”

(3) GNN

GNN consists of multiple…

• 1) permutation “invariant” layers
• 2) permutation “equivariant” layers

( but naive MLP’s do not meet those conditions! )

So, how to design “invariant & equivariant” layers?

6-3. GCN (Graph Convolution Networks)

(1) Basic Idea

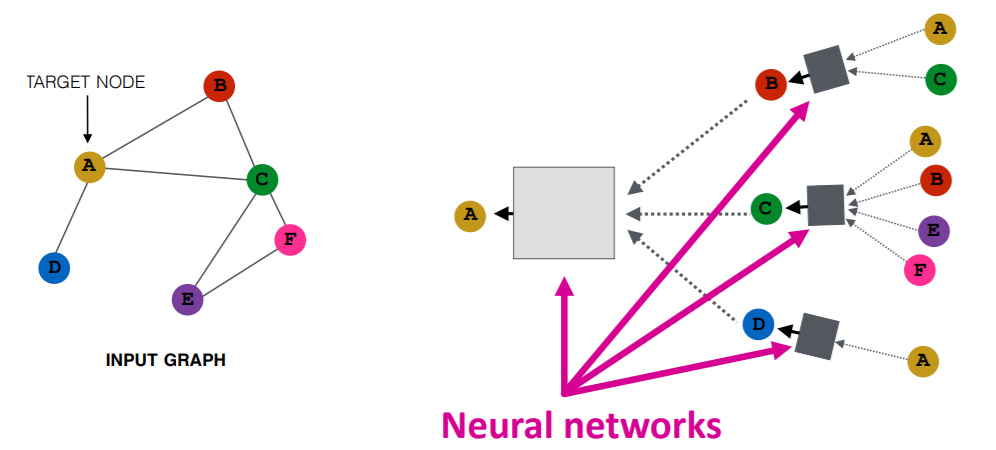
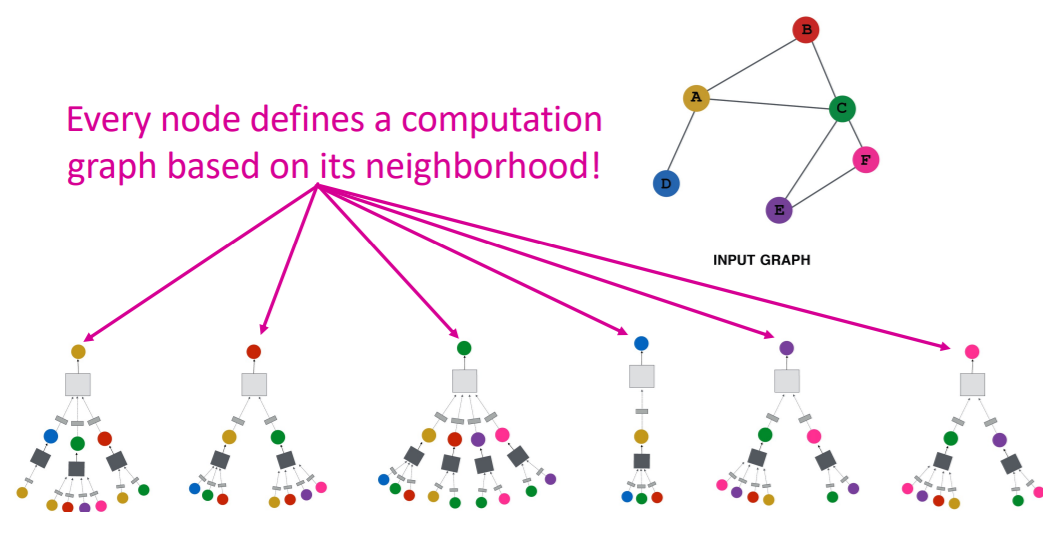
• Node’s neighborhood defines a computation graph
• so, how to propagate neighbor’s information?

Let’s generate node embeddings,

• based on “LOCAL NETWORK NEIGHBORHOOD”
• by using NN

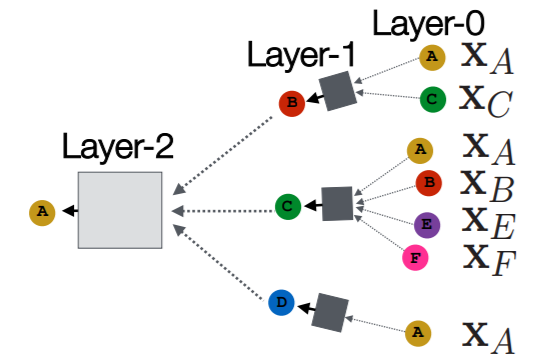
(2) Depth of NN

meaning of “Depth” ( of layers )

• layer 0 : target node itself
• layer 1 : 1-hop neighbors
• …
• layer \(K\) : \(K\)-hops neighbors

(3) Neighborhood aggregation

Procedure

• step 1) average messages of neighbors

• step 2) apply NN

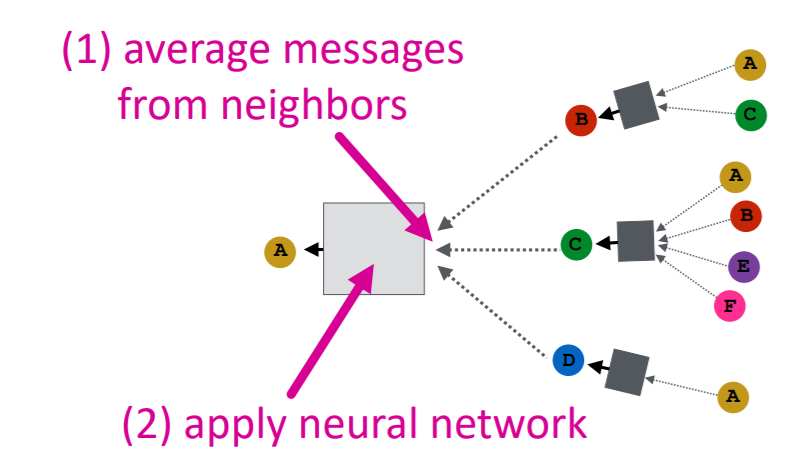
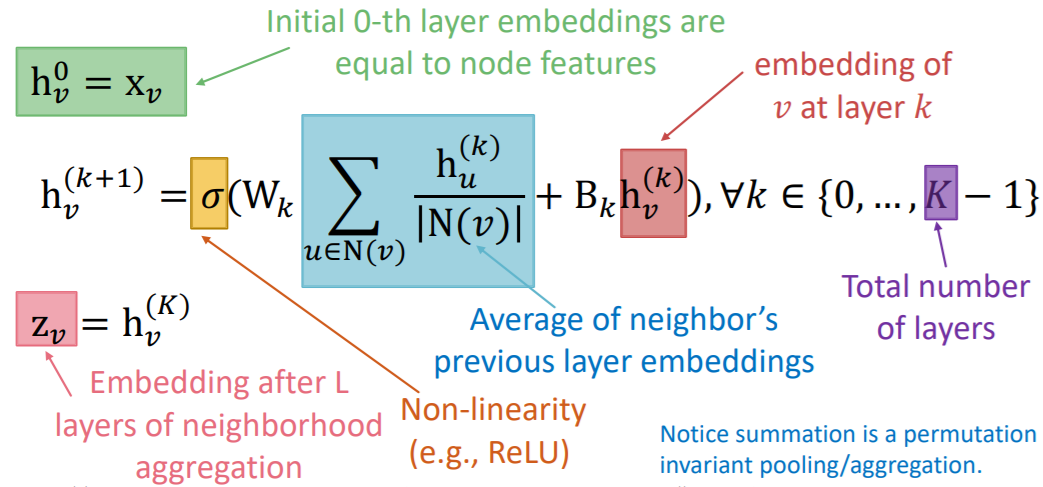
Both steps are “permutation equivariant”

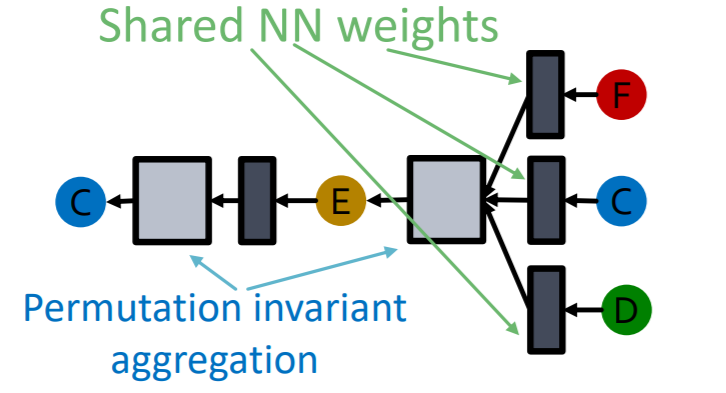
(4) Training GCN

2 big steps

• 1) defining “neighborhood aggregation” function
• 2) defining “loss function”

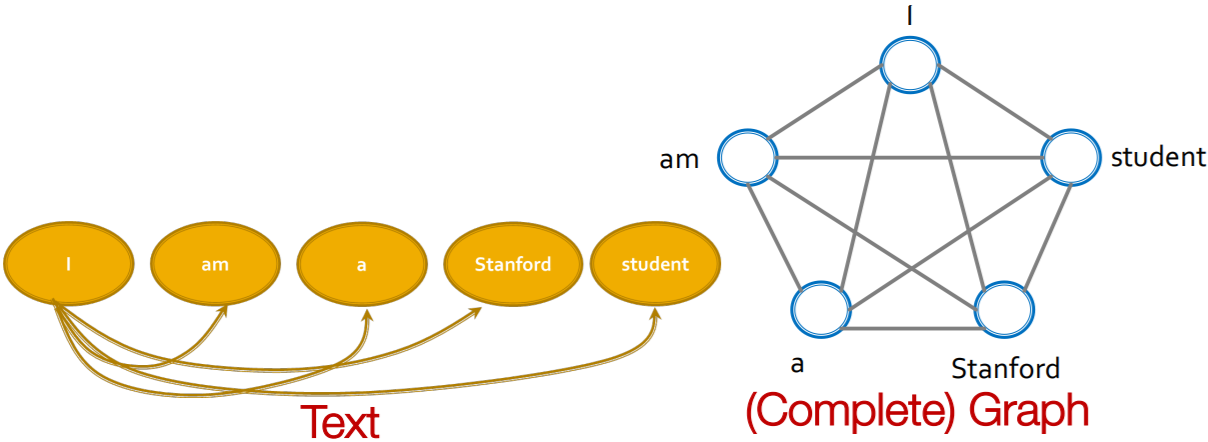
Notation

• \(h_v^k\) : hidden representation of \(v\) at layer \(k\)
  • \(W_k\) : parameter for “neighborhood aggregation”
  • \(B_k\) : parameter for “transforming itself”

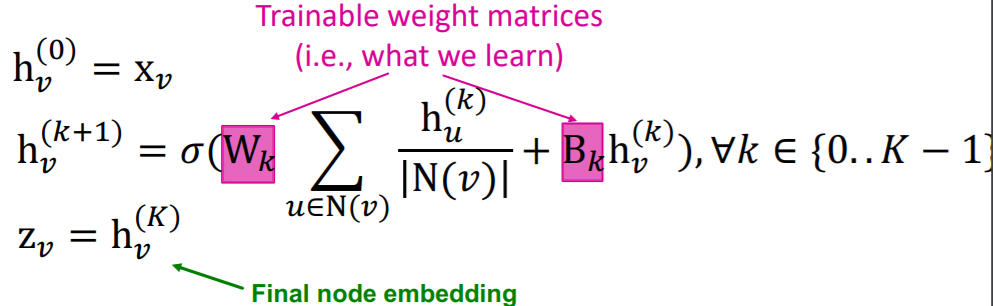
(5) Matrix Formulation

We can solve the above, by “matrix formulation”

• (vector) \(\sum_{u \in N(v)} \frac{h_{u}^{(k-1)}}{\mid N(v) \mid}\).

• (matrix) \(H^{(k+1)}=D^{-1} A H^{(k)}\).

  • \(H^{(k)}=\left[h_{1}^{(k)} \ldots h_{ \mid V \mid }^{(k)}\right]^{\mathrm{T}}\).

    ( thus, \(\sum_{u \in N_{v}} h_{u}^{(k)}=\mathrm{A}_{v,:} \mathrm{H}^{(k)}\) )

  • \(D_{v, v}=\operatorname{Deg}(v)= \mid N(v) \mid\).

Updating Function

\(H^{(k+1)}=\sigma\left(\tilde{A} H^{(k)} W_{k}^{\mathrm{T}}+H^{(k)} B_{k}^{\mathrm{T}}\right)\).

• where \(\tilde{A}=D^{-1} A\)
• term 1) \(\tilde{A} H^{(k)} W_{k}^{\mathrm{T}}\) :neighborhood aggregation
• term 2) \(H^{(k)} B_{k}^{\mathrm{T}}\) : self-transformation

Unsupervised Training

Loss Function :

\(\mathcal{L}=\sum_{z_{u}, z_{v}} \operatorname{CE}\left(y_{u, v}, \operatorname{DEC}\left(z_{u}, z_{v}\right)\right)\).

• \(y_{u,v}=1\), if \(u\) and \(v\) is similar
• example of \(DEC\) : inner product

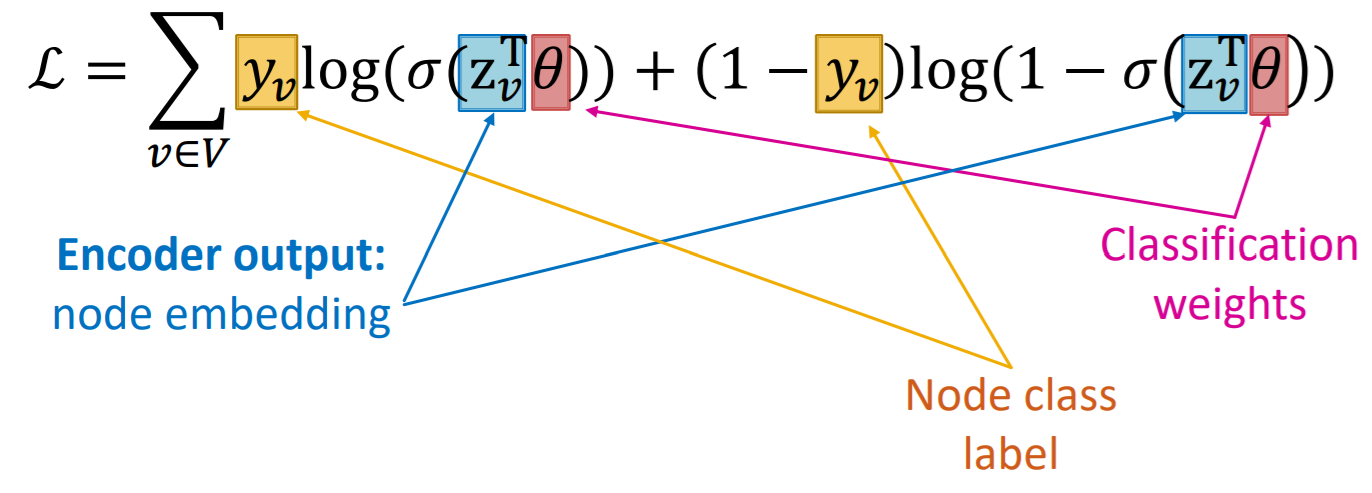
Supervised Training

just train as simple classification task!

( with CE loss )

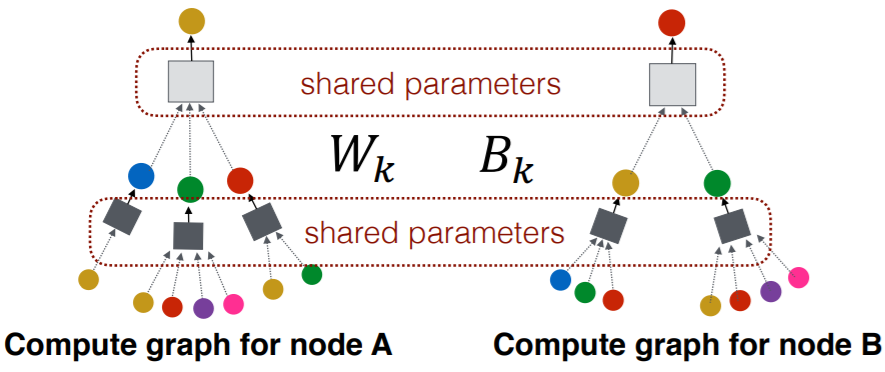
General Training procedure

dataset : batch of sub-graphs

procedure

• 1) train on a set of nodes
• 2) generate embedding “for all nodes”

Note

• “same” aggregation parameters for “all nodes”

  \(\rightarrow\) can generalize to UNSEEN nodes

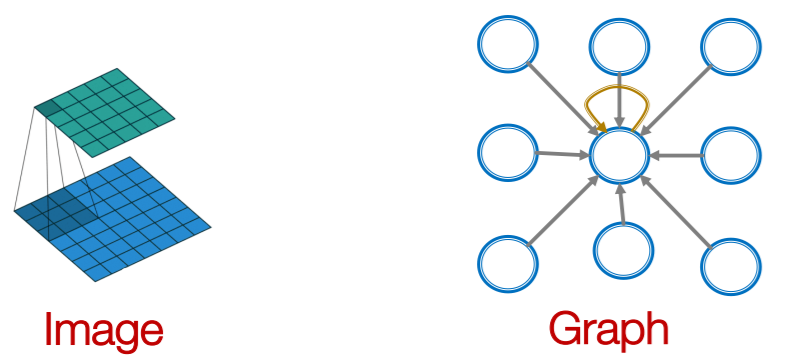
6-4. GNN vs CNN

GNN :

• \(\mathrm{h}_{v}^{(l+1)}=\sigma\left(\mathbf{W}_{l} \sum_{u \in \mathrm{N}(v)} \frac{\mathrm{h}_{u}^{(l)}}{ \mid \mathrm{N}(v) \mid }+\mathrm{B}_{l} \mathrm{~h}_{v}^{(l)}\right), \forall l \in\{0, \ldots, L-1\}\).

CNN :

• \(\mathrm{h}_{v}^{(l+1)}=\sigma\left(\sum_{u \in \mathrm{N}(v)} \mathbf{W}_{l}^{u} \mathrm{~h}_{u}^{(l)}+\mathrm{B}_{l} \mathrm{~h}_{v}^{(l)}\right), \forall l \in\{0, \ldots, L-1\}\).

Intuition

• learn “DIFFERENT” \(W_l\) for “DIFFERENT” neighbors in CNN,

  but not in GNN

  ( \(\because\) can pick an “ORDER” of neighbors, using “RELATIVE position”)

• can think of CNN as an “special GNN, with fixed neighbor size & ordering”

6-5. GNN vs Transformer

Transformer :

• can be seen as a special GNN that “runs on a fully connected word graph”