[ 7.Graph Neural Networks 2 ]
( 참고 : CS224W: Machine Learning with Graphs )
Contents
- 7-1. Introduction
- 7-2. Single GNN Layer
- 7-3. Types of GNN Layers
- 7-4. General GNN Layers
- 7-5. Stacking GNN Layers
7-1. Introduction
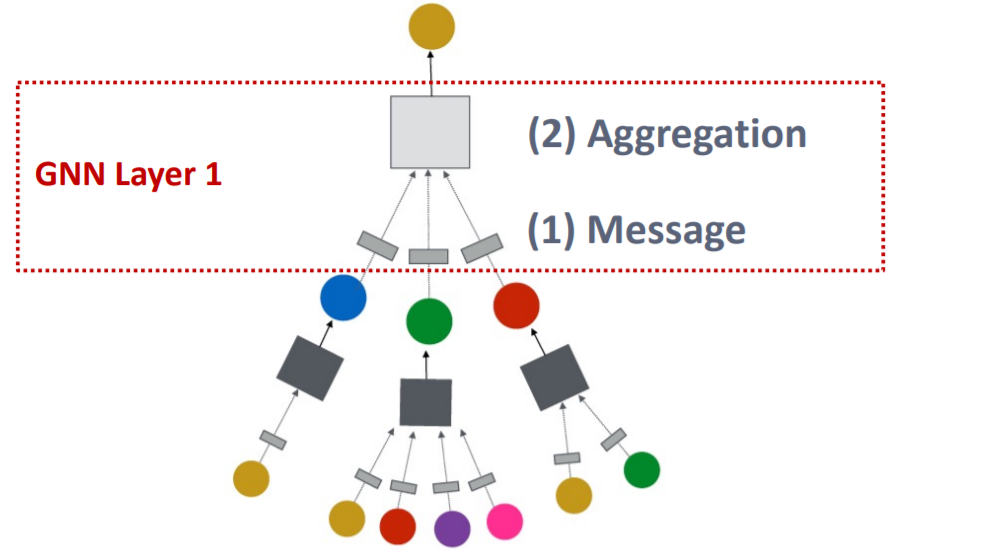
GNN Layer : consists of 2 main parts
- 1) message COMPUTATION
- 2) message AGGERGATION
After we have composed GNN Layer…..
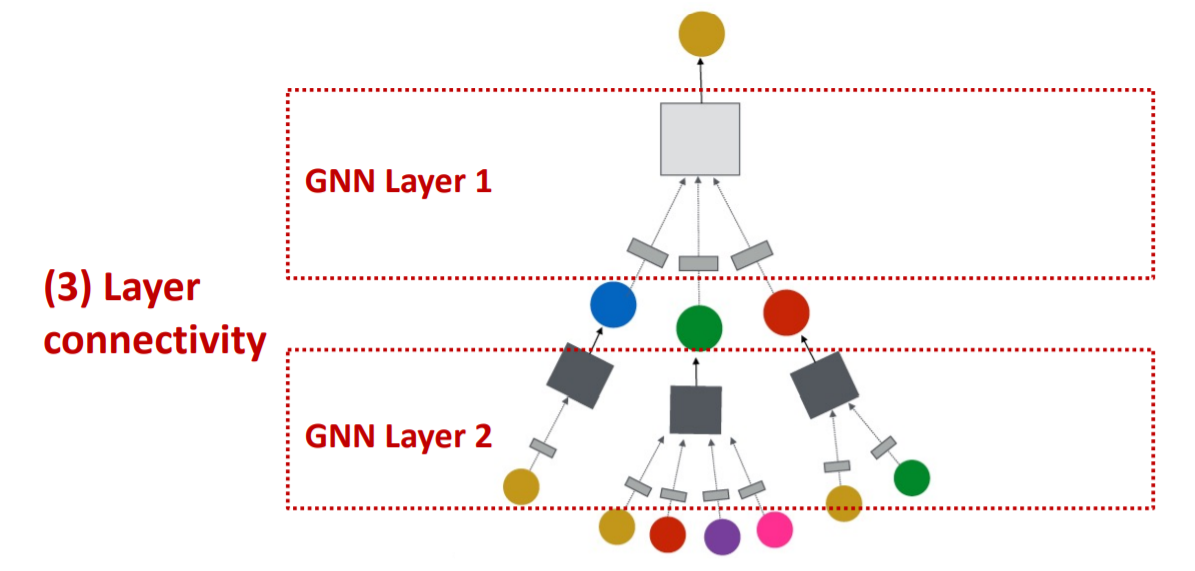
how to compose multiple GNN layers?
- 3) Layer Connectivity
After that… will talk about..
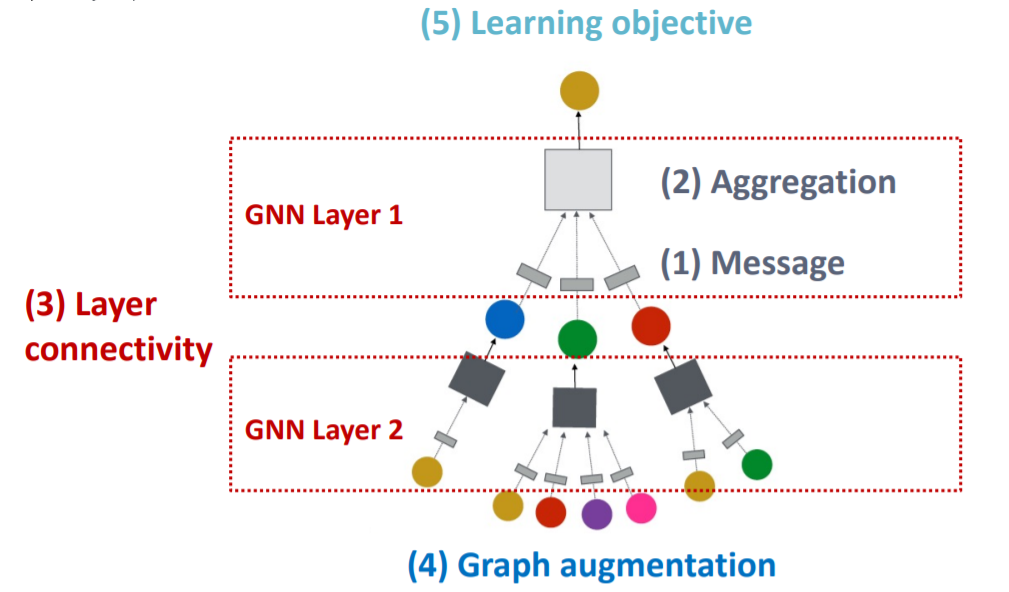
- 4) Graph Augmentation
- 4-1) Graph FEATURE augmentation
- 4-2) Graph STRUCTURE augmentation
Lastly, will cover
- 5) Learning Objective
Total Framework :
7-2. Single GNN Layer
Single GNN Layer consists of 2 steps
- 1) Message computation
- how to make each neighborhood node as embedding…
- 2) Message aggregation
- and how to combine those embeddings
- ( of course, the target node itself can also be an input! )
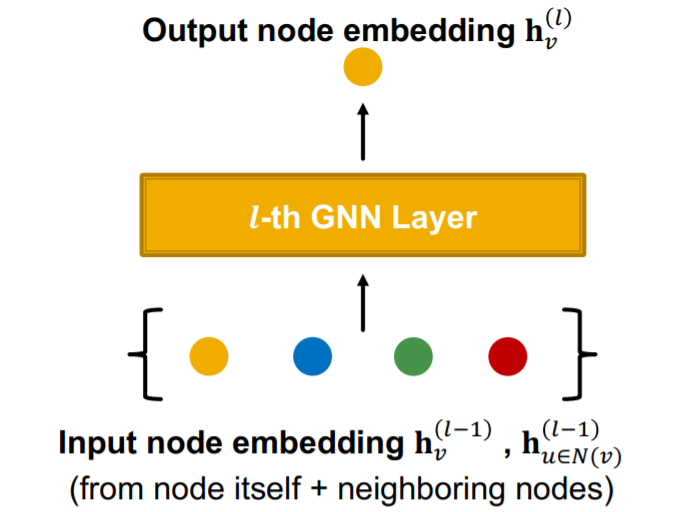
1) Message Computation
\(\mathbf{m}_{u}^{(l)}=\operatorname{MSG}^{(l)}\left(\mathbf{h}_{u}^{(l-1)}\right)\).
- function \(\text{MSG}\)?
- ex) Linear Layer : \(\mathbf{m}_{u}^{(l)}=\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\)
2) Message Aggregation
\(\mathbf{h}_{v}^{(l)}=\mathrm{AGG}^{(l)}\left(\left\{\mathbf{m}_{u}^{(l)}, u \in N(v)\right\}\right)\).
-
function \(\text{AGG}\)?
-
ex) sum / mean / max
\(\mathbf{h}_{v}^{(l)}=\operatorname{Sum}\left(\left\{\mathbf{m}_{u}^{(l)}, u \in N(v)\right\}\right)\).
-
Problem ( Issue ) : information of the target node ITSELF can be lost!
Solution :
-
1) message computation
- compute the message of target node itself
- ex) neighborhood node : \(\mathbf{m}_{u}^{(l)}=\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\)
- ex) target node : \(\mathbf{m}_{v}^{(l)}=\mathbf{B}^{(l)} \mathbf{h}_{v}^{(l-1)}\)
- compute the message of target node itself
-
2) message aggregation
-
ex) concatenation / summation :
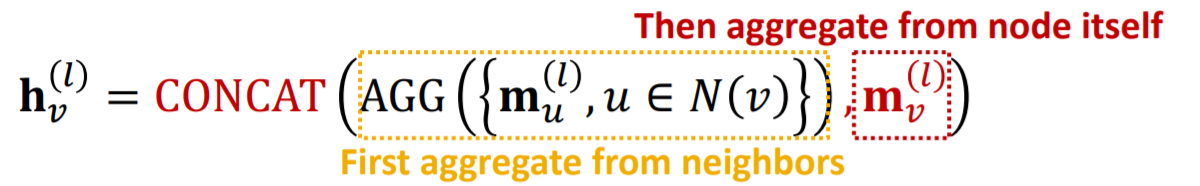
-
7-3. Types of GNN Layers
1) GCN
-
expression 1)
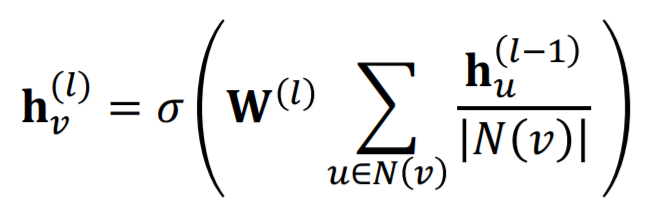
-
expression 2) as “message COMPUTATION” + “message AGGREGATION”
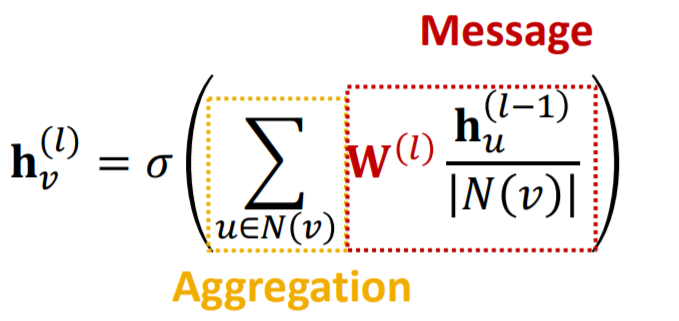
- meaning :
- 1) message COMPUTATON : \(\mathbf{m}_{u}^{(l)}=\frac{1}{ \mid N(v) \mid} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\).
- 2) message AGGREGATION : \(\mathbf{h}_{v}^{(l)}=\sigma\left(\operatorname{Sum}\left(\left\{\mathbf{m}_{u}^{(l)}, u \in N(v)\right\}\right)\right)\).
- meaning :
2) GraphSAGE
GCN vs GraphSAGE
- GCN : \(\mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)} \mathbf{W}^{(l)} \frac{\mathbf{h}_{u}^{(l-1)}}{\mid N(v) \mid }\right)\)
- GraphSAGE : \(\mathbf{h}_{v}^{(l)}=\sigma\left(\mathbf{W}^{(l)} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{v}^{(l-1)}, \operatorname{AGG}\left(\left\{\mathbf{h}_{u}^{(l-1)}, \forall u \in N(v)\right\}\right)\right)\right)\).
To decompose GraphSAGE …
-
1) message COMPUTATION : aggregate from node neighbors
-
\(\mathbf{h}_{N(v)}^{(l)} \leftarrow \mathrm{AGG}\left(\left\{\mathbf{h}_{u}^{(l-1)}, \forall u \in N(v)\right\}\right)\).
-
AGG function :
-
1) mean : \(\begin{gathered} A G G= \end{gathered} \sum_{u \in N(v)} \frac{\mathbf{h}_{u}^{(l-1)}}{ \mid N(v) \mid }\)
-
2) pool : \(\mathrm{AGG}=\operatorname{Mean}\left(\left\{\operatorname{MLP}\left(\mathbf{h}_{u}^{(l-1)}\right), \forall u \in N(v)\right\}\right)\).
-
3) lstm : \(AGG =\operatorname{LSTM}\left(\left[\mathbf{h}_{u}^{(l-1)}, \forall u \in \pi(N(v))\right]\right)\)
-
-
-
2) message AGGREGATION : aggregate over the node itself
- \(\mathbf{h}_{v}^{(l)} \leftarrow \sigma\left(\mathbf{W}^{(l)} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{v}^{(l-1)}, \mathbf{h}_{N(v)}^{(l)}\right)\right)\).
3) Graph Attention Networks
\(\mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)} \alpha_{v u} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)\).
- attention weight in GCN / GraphSAGE :
- \(\alpha_{v u}=\frac{1}{ \mid N(v) \mid }\) : node u’s message to node v
- why not learn “attention weight”?
- attention coefficient : \(e_{v u}=a\left(\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}, \mathbf{W}^{(l)} \boldsymbol{h}_{v}^{(l-1)}\right)\).
- attention weight : \(\alpha_{v u}=\frac{\exp \left(e_{v u}\right)}{\sum_{k \in N(v)} \exp \left(e_{v k}\right)}\).
- weighted sum, based on attention weight : \(\mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)} \alpha_{v u} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)\).
what to use as \(a\) function?
-
ex) single NN
- \(\begin{aligned} &e_{A B}=a\left(\mathbf{W}^{(l)} \mathbf{h}_{A}^{(l-1)}, \mathbf{W}^{(l)} \mathbf{h}_{B}^{(l-1)}\right) =\text { Linear }\left(\text { Concat }\left(\mathbf{W}^{(l)} \mathbf{h}_{A}^{(l-1)}, \mathbf{W}^{(l)} \mathbf{h}_{B}^{(l-1)}\right)\right) \end{aligned}\).
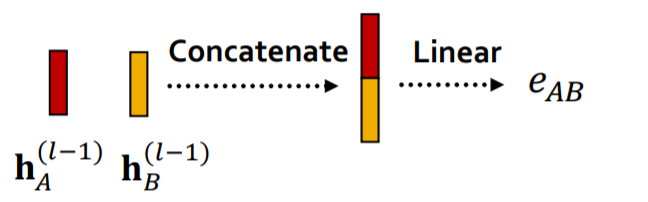
Multi-head attention
ex) 3 heads :
- \(\mathbf{h}_{v}^{(l)}[1]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{1} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)\).
- \(\mathbf{h}_{v}^{(l)}[2]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{2} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)\).
- \(\mathbf{h}_{v}^{(l)}[3]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{3} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)\).
- then……aggregate by “concatenation or summation”
- \(\mathbf{h}_{v}^{(l)}=\) AGG \(\left(\mathbf{h}_{v}^{(l)}[1], \mathbf{h}_{v}^{(l)}[2], \mathbf{h}_{v}^{(l)}[3]\right)\)
Benefits of attention?
- key : different importance for different neighbors
- 1) computationally efficient
- attentional coefficients : can be computed in PARALLEL
- 2) storage efficient
- fixed number of params ( \(O(V+E)\) entries to be stored )
- 3) localized
- attention over LOCAL NETWORK neighborhood
- 4) inductive capacity
- shared EDGE-wise mechanism
7-4. General GNN Layers
can use modern DL techniques
- 1) Batch Norm
- 2) Dropout
- 3) Attention & Gating
7-5. Stacking GNN Layers
how to construct GNN?
- stack GNN layers sequentially!
- input : raw node feature ( \(\mathrm{x}_{v}\) )
- output : NODE EMBEDDINGS ( \(\mathbf{h}_{v}^{(L)}\) ) …….. ( after \(L\) GNN Layers )
Over-smoothing Problem
-
over-smoothing : all nodes have similar embeddings
-
reason : TOO MANY GNN LAYERS
( think of receptive field! )
the more GNN layers, the larger receptive field!
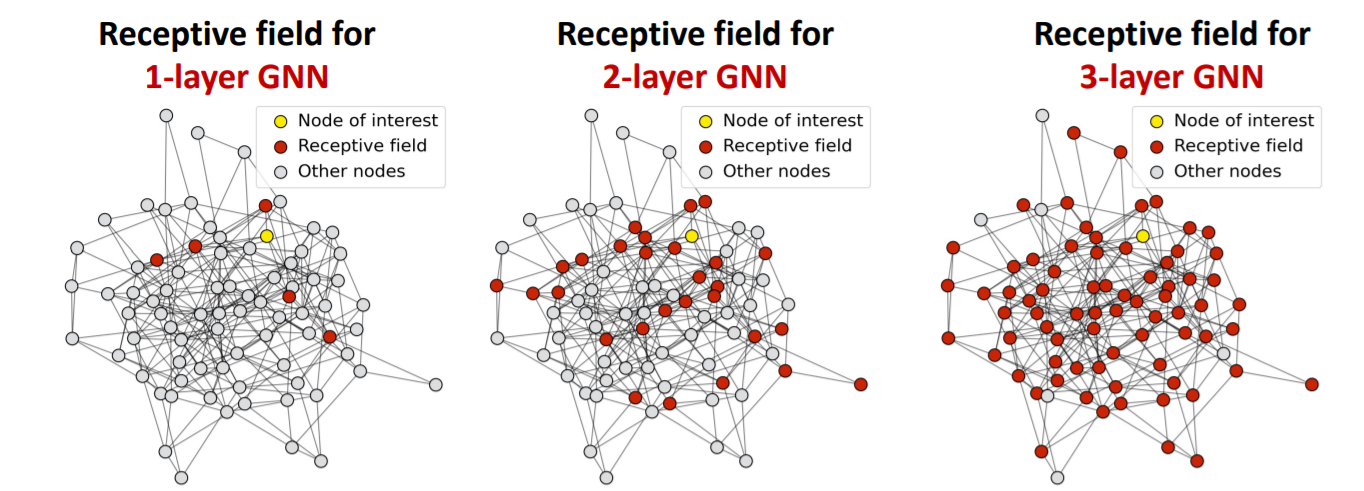
- deeper GNN layers \(\rightarrow\) shared number of neighbors \(\uparrow\)
So, how to overcome?
-
solution 1) Increase the expressive power WITHIN each GNN layer
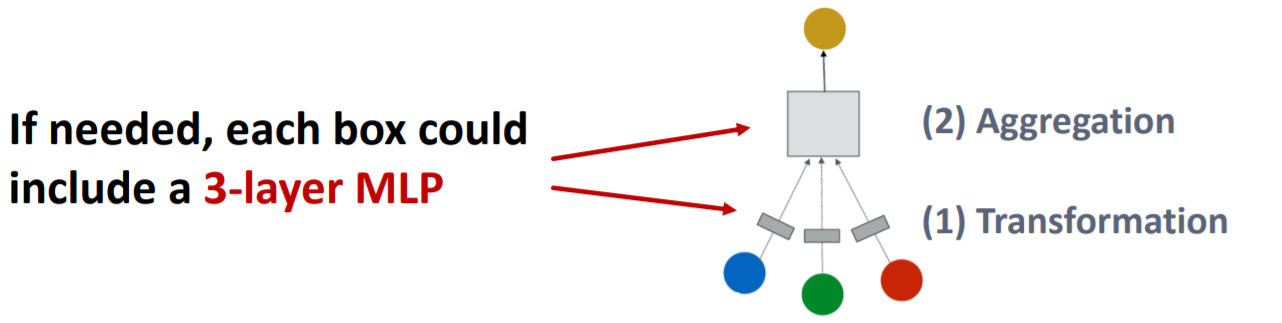
-
solution 2) Add layers that DO NOT PASS MESSAGES
- ex) skip connection

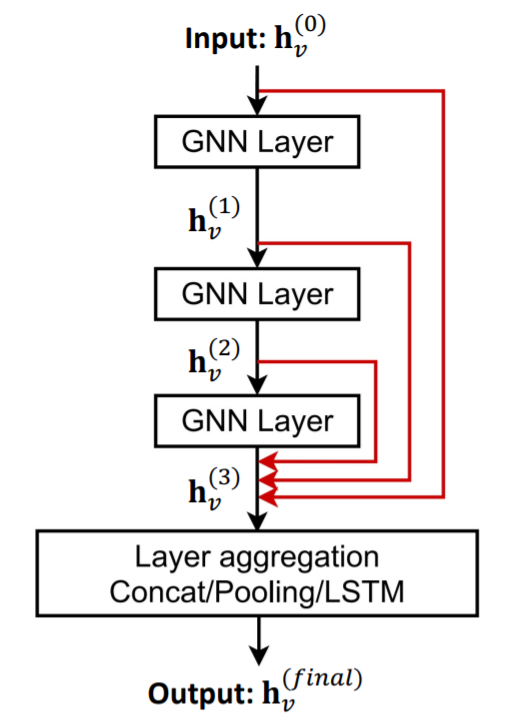
Skip-connections
but…to use many layers…
- \(N\) skip connections \(\rightarrow\) \(2^N\) possible paths
- meaning : mixture of “SHALLOW & DEEP” GNNs
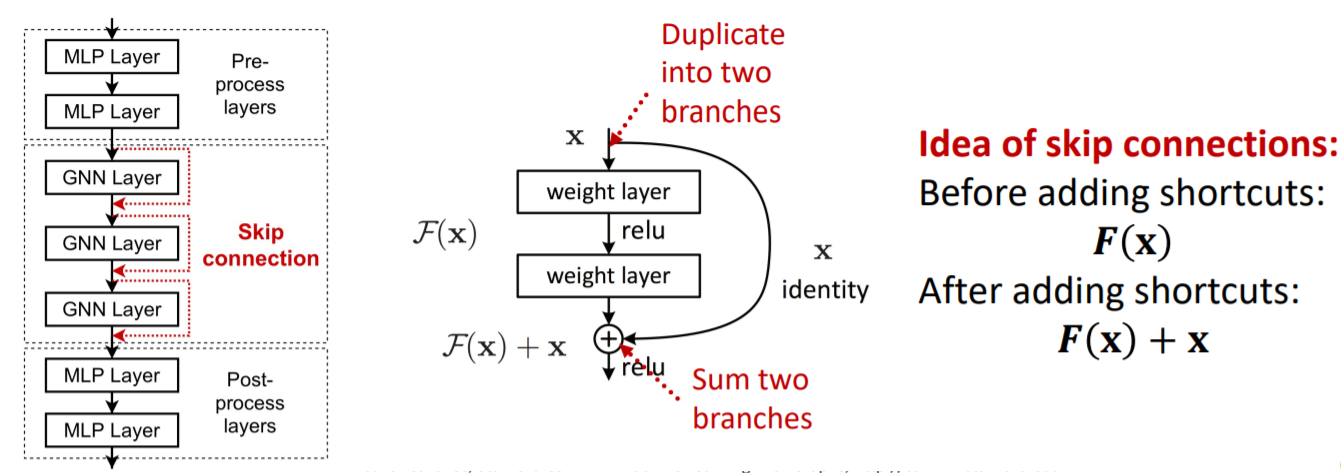
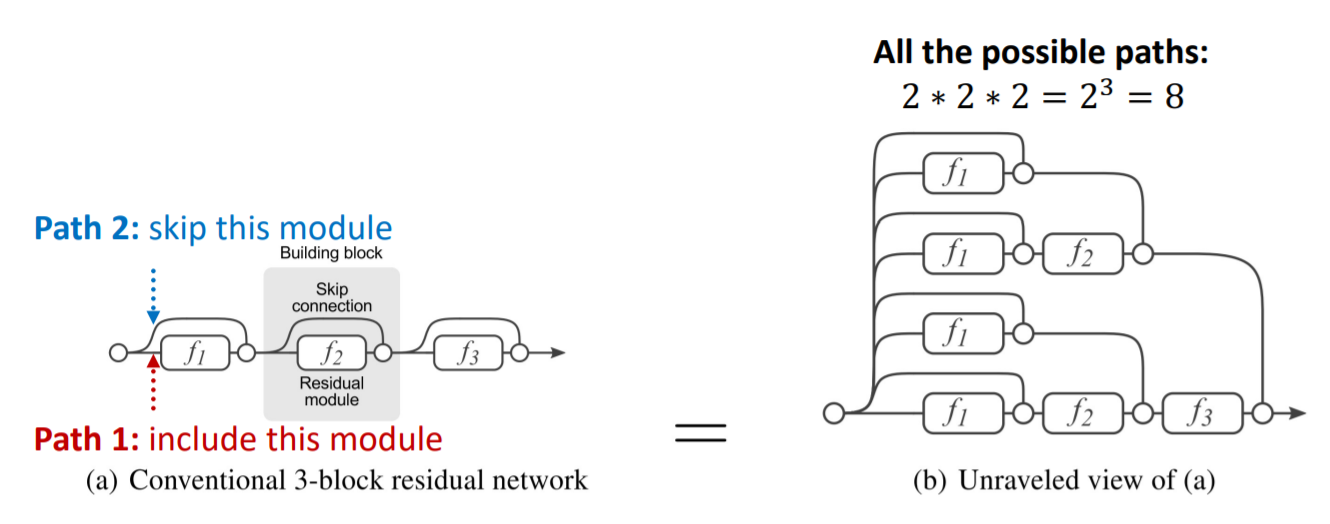
Standard GCN
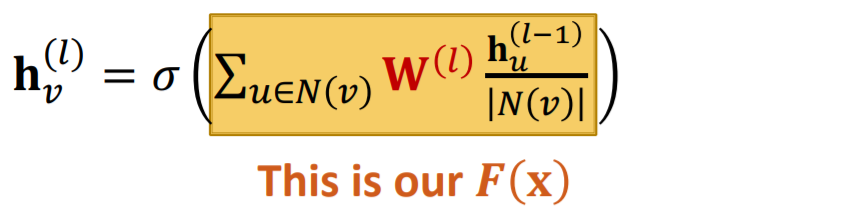
GCN + Skip Connection
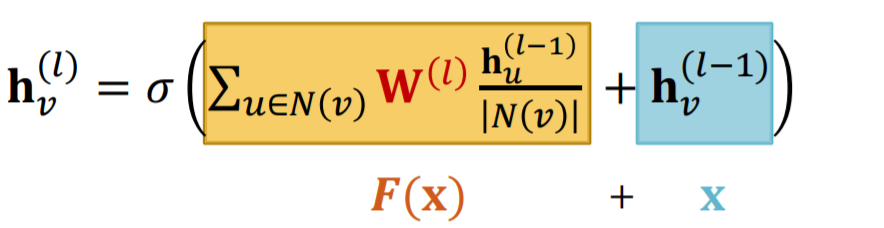
Other options
- final layers : aggregates from the all the node embeddings in the previous layers