[ 9.Theory of GNNs ]
( 참고 : CS224W: Machine Learning with Graphs )
Contents
- 9-1. How Expressive are GNNs?
- 9-2. Designing the most powerful GNN
9-1. How Expressive are GNNs?
GNN models
-
key point : aggregate information form neighbors using NN
-
ex) GCN, GAT, GraphSage, …
- different models use different NN in the box below!
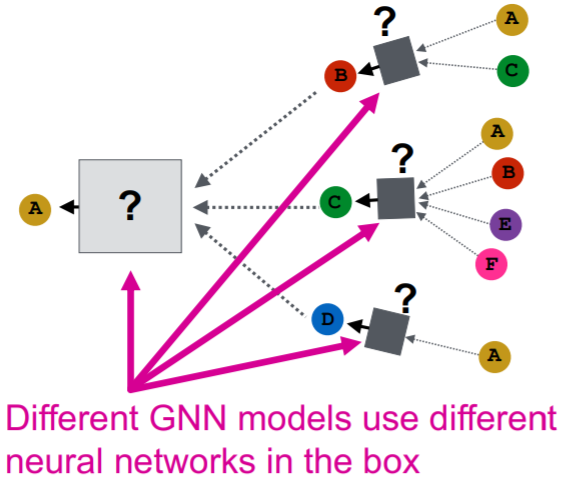
Example
- GCN : mean pooling
- GraphSAGE : max pooling
notation
-
use “node colors” as “node features”
( same color = same feature )
Question : how well can GNN distinguish different graph structures?
(1) Local Neighborhood Structures
node A & B haver DIFFERENT neighborhood structure , because…
- ex 1) because they have “different node degrees”
- ex 2) even though they have same degree, “their neighbors have different node degrees”
node A & B haver SAME neighborhood structure , because…
- ex 3) they are “symmetric within the graph”
how does GNN captures “local neighborhood structures”?
\(\rightarrow\) key : “Computational Graph”
(2) Computational Graph
GNN aggregates “neighbors’ node embedding”,
- by “computational graph”
example :
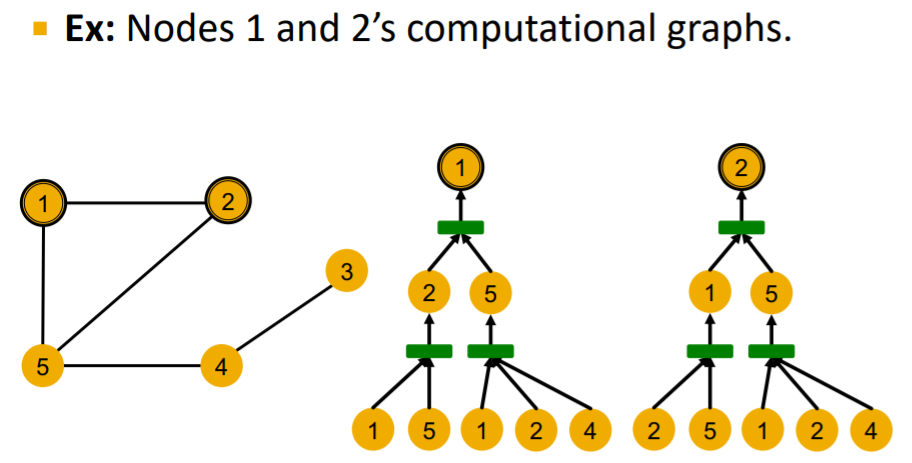
Two computational graphs above are identical!
- only sees the node features, not node IDs!
- \(\rightarrow\) thus, “SAME embedding” ( unable to distinguish )
Computational graphs are identical to “rooted subtree structures” around each node
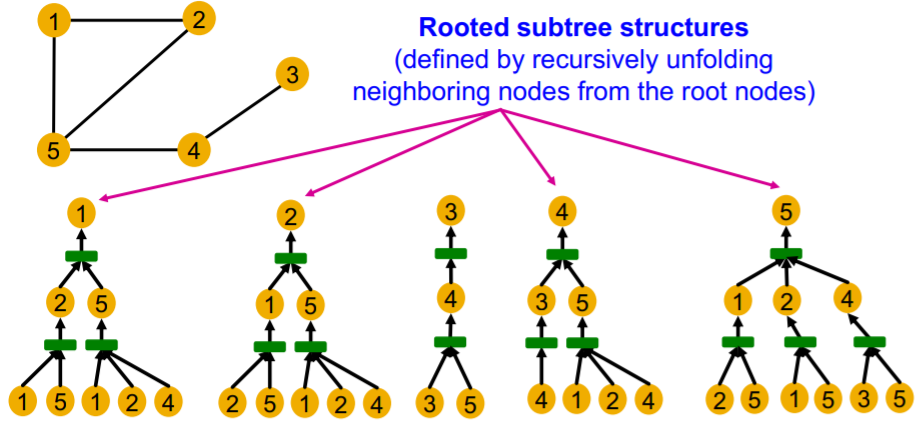
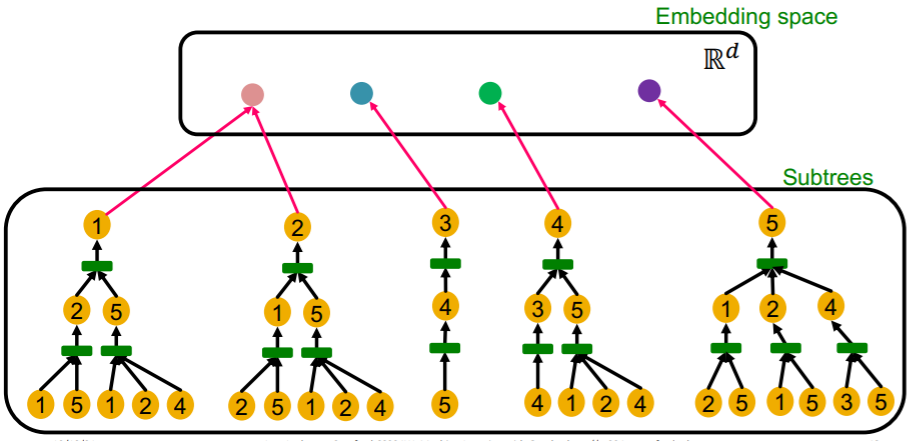
Expressive GNN :
-
= maps “different rooted subtrees” to “different node embeddings”
= maps subtrees to the node embeddings “INJECTIVELY”
( injective : map different elements into different outputs )
-
If each step of GNN’s aggregation can fully retain the neighboring information, the generated node embeddings can distinguish different rooted subtrees.
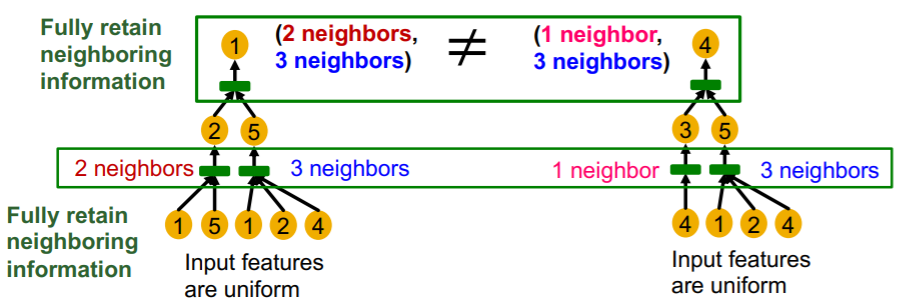
9-2. Designing the most powerful GNN
key point : neighbor aggregation functions
-
neighborhood aggregation function
= function over a multi-set
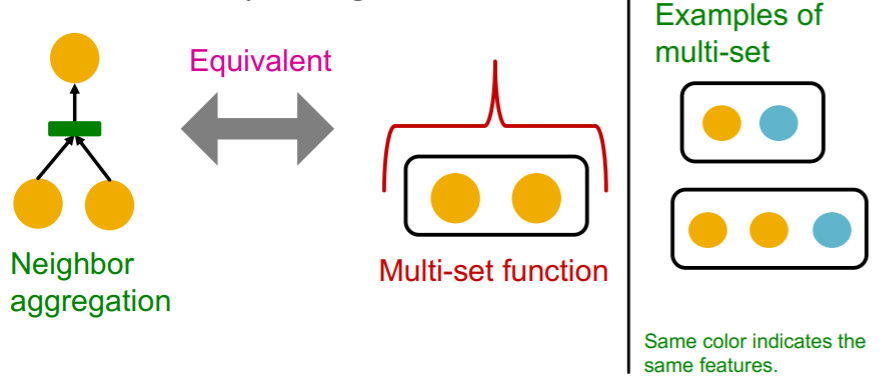
(1) Aggregation Functions
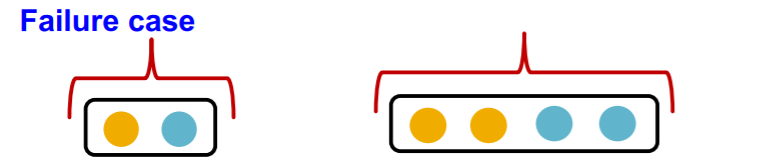
(a) GCN : mean-pool ( element-wise )
-
\(\operatorname{Mean}\left(\left\{x_{u}\right\}_{u \in N(v)}\right)\).
-
failure case :
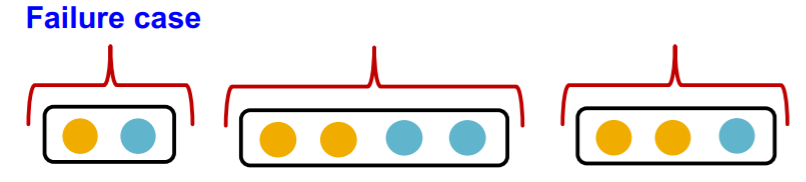
(b) GraphSAGE : max-pool ( element-wise )
-
\(\operatorname{Max}\left(\left\{x_{u}\right\}_{u \in N(v)}\right)\).
-
failure case :
Both are “NOT INJECTIVE”
\(\rightarrow\) not maximally powerful GNNs!
So, how to make expressive GNNs?
( = how to design “injective neighborhood aggregation function”? )
(2) Injective Multi-set Function
can be expressed as…
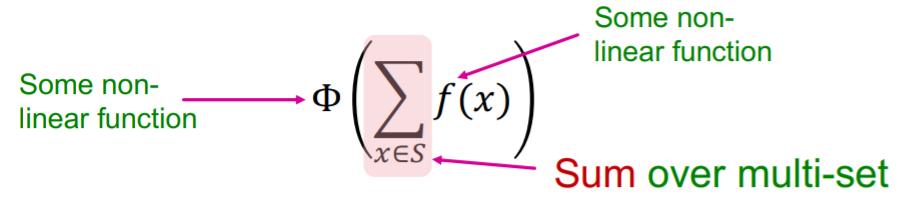
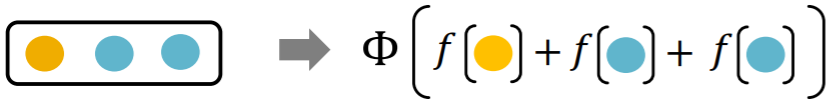
- use MLP as \(\phi\) & \(f\)……. GIN
(3) GIN (Graph Isomorphism Network)
\(\operatorname{MLP}_{\Phi}\left(\sum_{x \in S} \operatorname{MLP}_{f}(x)\right)\).
- INJECTIVE aggregation function
- the most expressive GNN
full model of GIN
-
relate to WL graph kernel ( = color refinement algorithm )
- step 1) assign initial color \(c^{(0)}(v)\) to each node
- step 2) iteratively refine node colors…
- \(c^{(k+1)}(v)=\operatorname{HASH}\left(c^{(k)}(v),\left\{c^{(k)}(u)\right\}_{u \in N(v)}\right)\).
- HASH function = different input \(\rightarrow\) different colors
- ( continues until a stable coloring is reached )
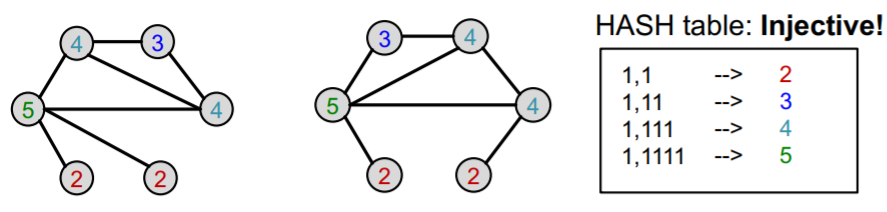
GIN uses “NN” as “injective HASH function”
- injective function over the tuple below
- 1) root node features
- 2) neighborhood node colors
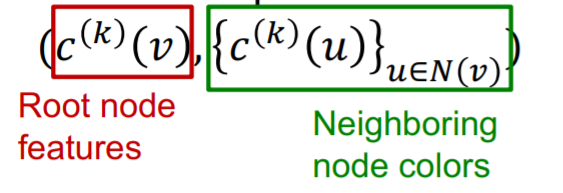
Model details :
\(\left.\operatorname{MLP}_{\Phi}\left((1+\epsilon) \cdot \operatorname{MLP}_{f}\left(c^{(k)}(v)\right)\right)+\sum_{u \in N(v)} \operatorname{MLP}_{f}\left(c^{(k)}(u)\right)\right)\).
- \(\epsilon\) : learnable scalar
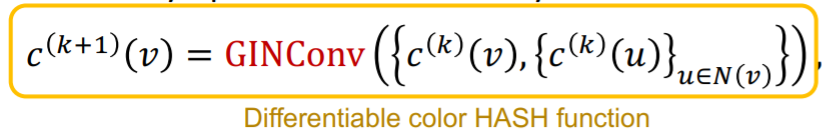
Summary
- GIN = differentiable NN version of WL graph kernel

