7. Graph Residual Networks (GRNs)
stack \(K\) GNNs
\(\rightarrow\) but, not too much performance improvement…
( \(\because\) also propagate noisy information, from too many neighbors )
Thus, use skip connections to solve the problem!
\(\rightarrow\) called GRNs ( Graph Residual Networks )
7-1. Highway GCN
Highway Network + GNN
-
in each layer, input is multiplied by gating weights
& summed with the output
- \(\mathbf{T}\left(\mathbf{h}^{t}\right) =\sigma\left(\mathbf{W}^{t} \mathbf{h}^{t}+\mathbf{b}^{t}\right)\).
- \(\mathbf{h}^{t+1} =\mathbf{h}^{t+1} \odot \mathbf{T}\left(\mathbf{h}^{t}\right)+\mathbf{h}^{t} \odot\left(1-\mathbf{T}\left(\mathbf{h}^{t}\right)\right)\).
Highway gates
- ability to select from NEW & OLD hidden states
- early hidden states can be propagetd to final state, if needed!
At most 4 layers ( not much difference afterwards.. )
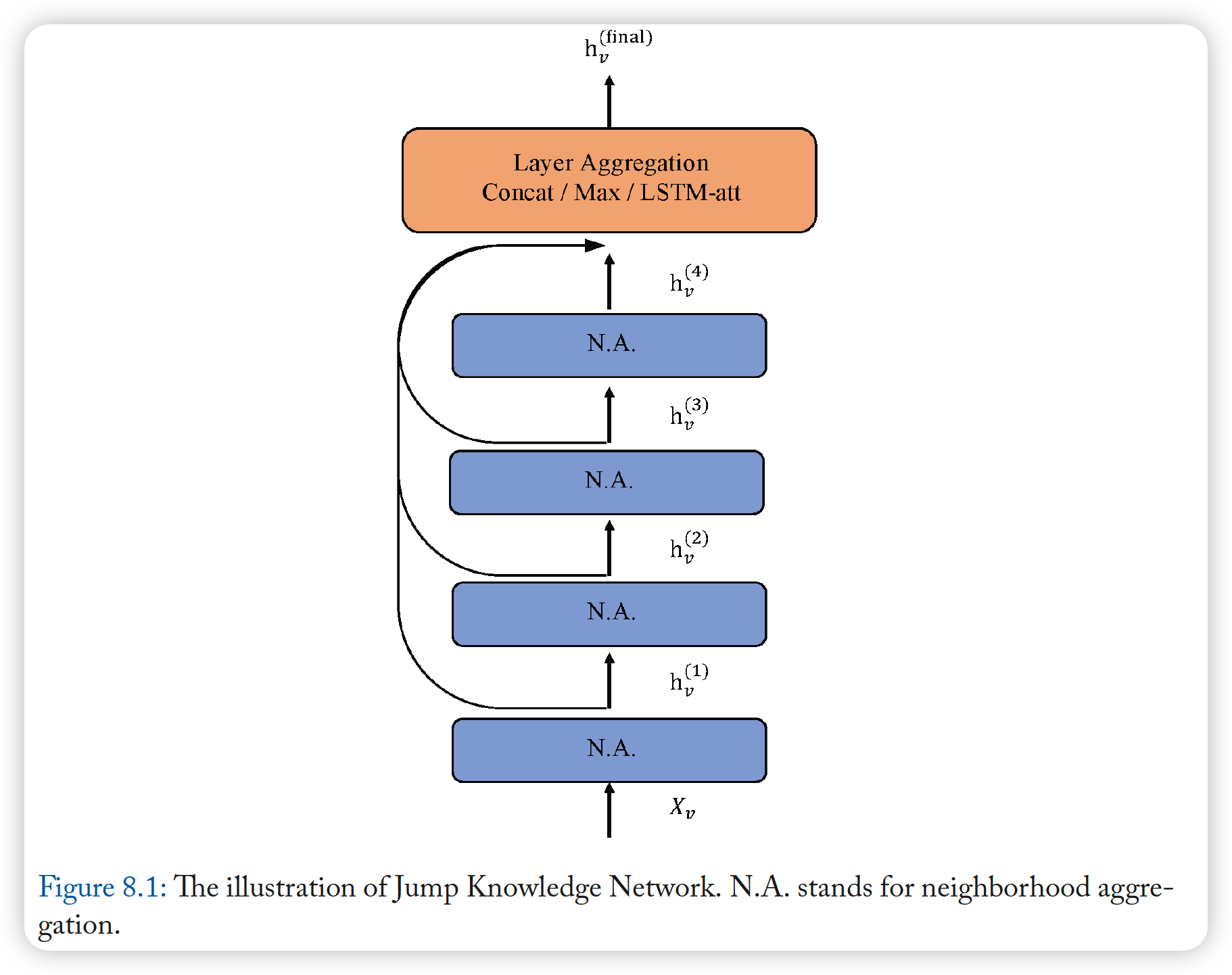
7-2. Jump Knowledge Network
Limitations of neighborhood aggregation
- different nodes in graphs, may need different receptive fields
- ex) core nodes : need many neighbors
- ex) node far from core : need less neighbors
Jump Knowledge Newtork
- adaptive, structure-aware representations
-
selects from all of intermediate representations
-
able to select effective neighborhood size
- can be cominbed with GCN, GraphSAGE, GAT..
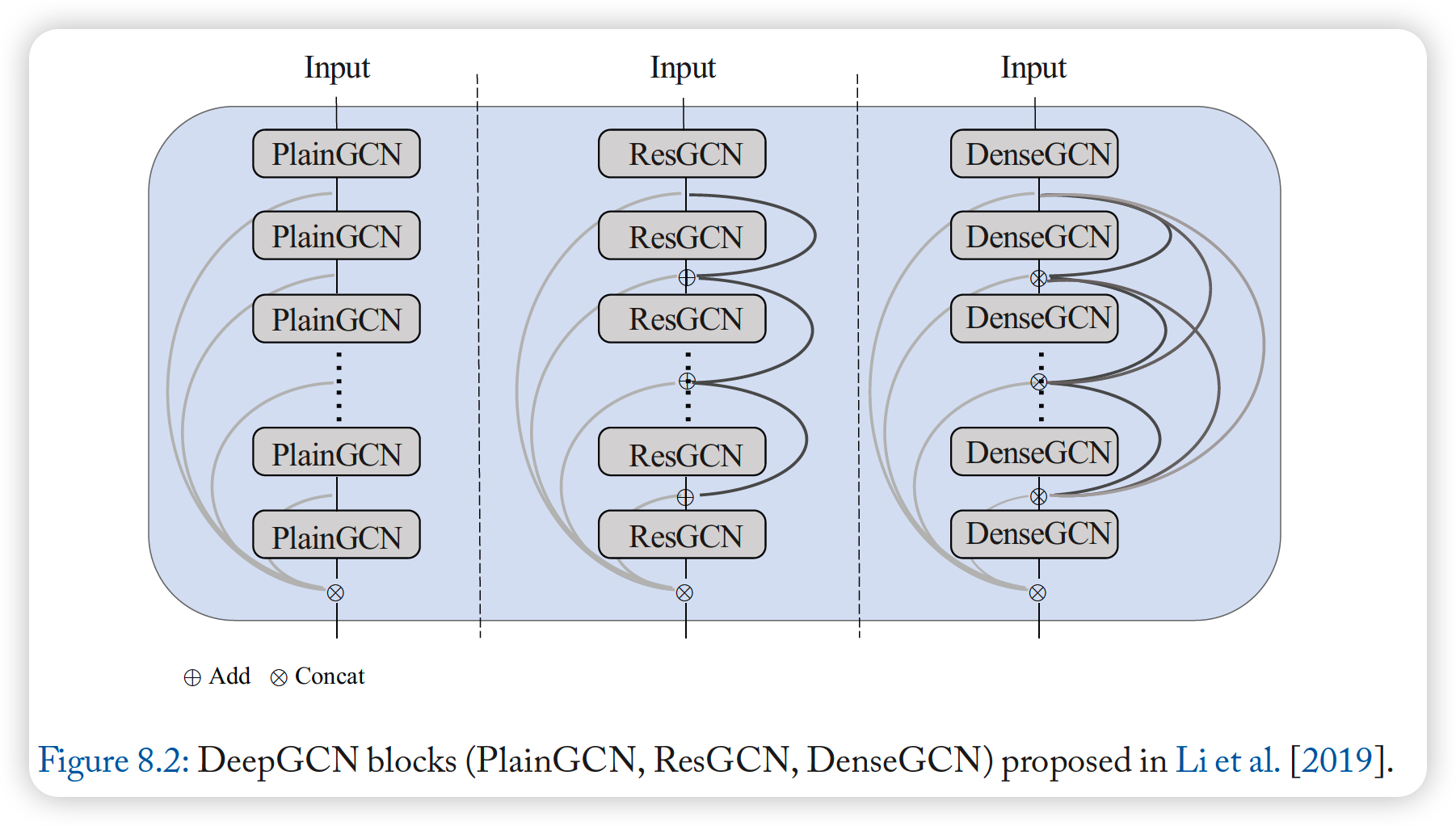
7-3. DeepGCNs
stacking more layers ….problem?
- (1) vanishing gradient
- (2) over-smoothing
Solution :
-
for problem (1) : use residual connections & dense connections
-
for problem (2) : use dilated CNN
3 types of GCN
- Plain GCN ( = Vanilla GCN )
- ResGCN
- DenseGCN
Plain GCN ( = Vanilla GCN )
- \(\mathbf{H}^{t+1}=\mathcal{F}\left(\mathbf{H}^{t}, \mathbf{W}^{t}\right)\).
ResGCN
- \(\mathbf{H}_{\text {Res }}^{t+1} =\mathbf{H}^{t+1}+\mathbf{H}^{t} =\mathcal{F}\left(\mathbf{H}^{t}, \mathbf{W}^{t}\right)+\mathbf{H}^{t}\).
DenseGCN
- \(\begin{aligned}
\mathbf{H}_{\text {Dense }}^{t+1} &=\mathcal{T}\left(\mathbf{H}^{t+1}, \mathbf{H}^{t}, \ldots, \mathbf{H}^{0}\right) \\
&=\mathcal{T}\left(\mathcal{F}\left(\mathbf{H}^{t}, \mathbf{W}^{t}\right), \mathcal{F}\left(\mathbf{H}^{t-1}, \mathbf{W}^{t-1}\right), \ldots, \mathbf{H}^{0}\right)
\end{aligned}\).
- \(\mathcal{T}\) : vertex wise concatenation
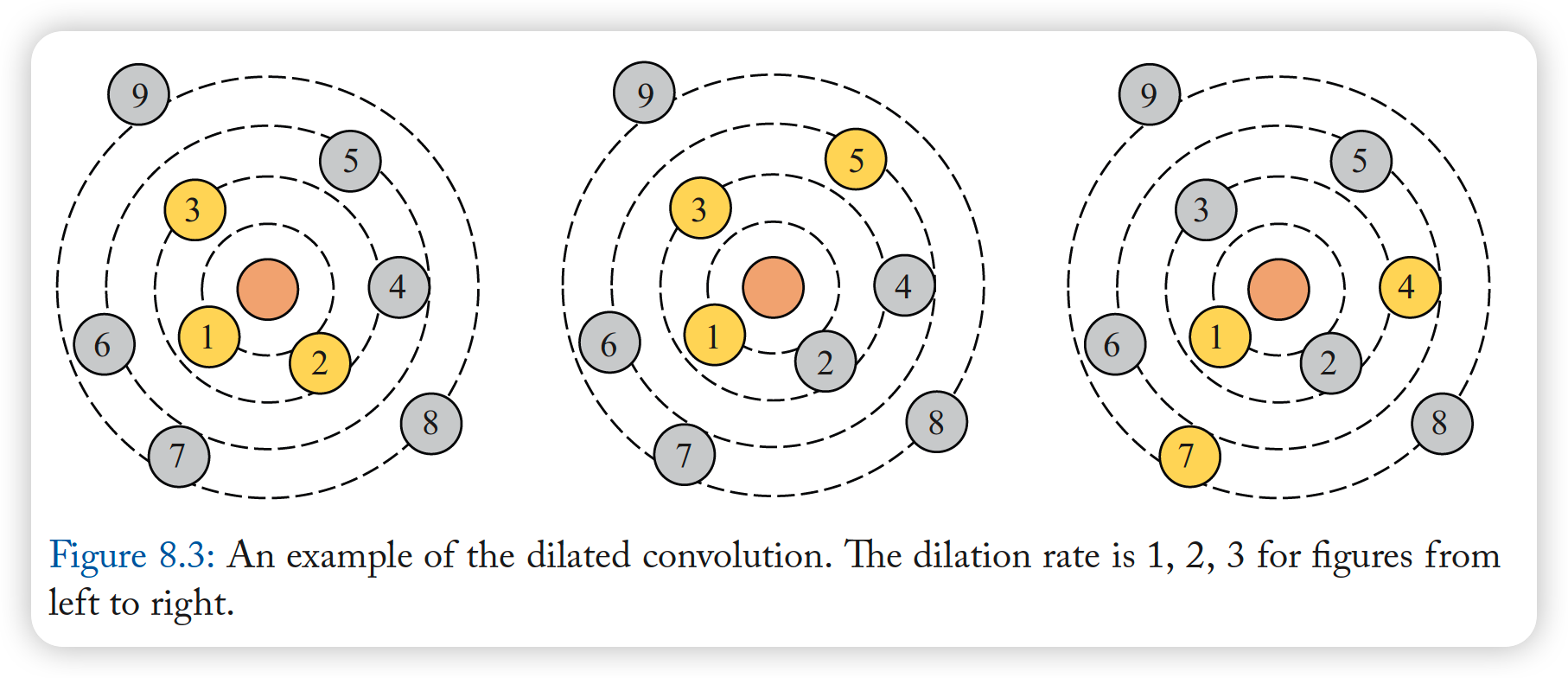
Dilated Convolutions
- to solve over smoothing
-
this paper uses Dilated k-NN
-
leverages information from different context
& able to enlarge receptive field
\(\rightarrow\) added to ResGCN, DenseGCN