[meta] (code review) Matching Networks

(code review) Matching Network

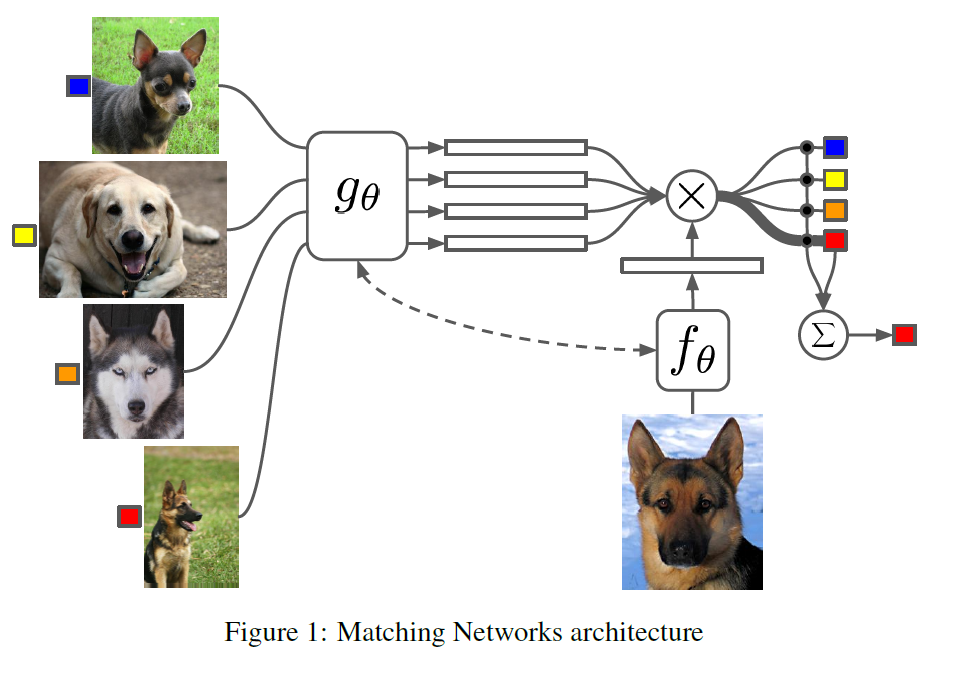
1. Task Sampler

• (1) 랜덤하게/고정되게 task를 샘플하기
  • ex) class A vs class D를 비교하는 task
• (2) 해당 task에 사용되는(=task의 class label을 가지는) 데이터셋 불러오기
  • ex) class A & class D에 해당하는 데이터셋
• (3) 불러온 두 데이터셋을 둘로 나눔
  • (a) Support Set ( ex. A1,A5,A9,…D1,D2,D6,.. )
  • (b) Query Set ( ex. A2,A3,A4,…,D3,D4,D5… )
• (4) 두 데이터셋에서 각각 n_shot개, num_Q개만큼을 샘플
  • (a 일부) Support Set 일부 ( ex. A1,A5,A13,A15 & D1,D6,D10,D11 )
  • (b 일부) Query Set 일부 ( ex. A3,A4 & D2,D7 )
• (5) (a 일부)+(b 일부) 합쳐서 return

class NShotTaskSampler(Sampler):
    def __init__(self,dataset,episodes_per_epoch,
                 n_shot,k_way,num_Q,num_tasks= 1,
                 fixed_tasks: List[Iterable[int]] = None):
        super(NShotTaskSampler, self).__init__(dataset)
        self.episodes_per_epoch = episodes_per_epoch
        self.dataset = dataset
        self.num_tasks = num_tasks
        self.k_way = k_way
        self.n_shot = n_shot
        self.num_Q = num_Q
        self.fixed_tasks = fixed_tasks
        self.task_idx = 0

    def __len__(self):
        return self.episodes_per_epoch

    def __iter__(self):
        # (1) unique한 class명
        class_names=self.dataset.df['class_id'].unique()
        
        # (2) 1번의 epsiode 동안
        for _ in range(self.episodes_per_epoch):
            id_batches = []
            for task in range(self.num_tasks):
                ## case 1) 랜덤 task의 class id(이름)들
                if self.fixed_tasks is None:
                    episode_classes = np.random.choice(class_names,self.k, replace=False)
                ## case 2) 정해진 task의 class id(이름)들
                else:
                    episode_classes = self.fixed_tasks[self.task_idx % len(self.fixed_tasks)]
                    self.task_idx += 1
				## df = 해당 class id들을 가진 dataset
                df = self.dataset.df[self.dataset.df['class_id'].isin(episode_classes)]
                support_k = {k: None for k in episode_classes}
                
                #-----------------------------------------------------------#
                # class_k1 : S (support) -> 이 중 "n_shot개"만을 sample할 것 
                # class_k2 : Q (query) -> 이 중 "num_Q개"만을 sample할 것
                # class_k1, class_k2 모두 "같은 class들", but 서로 다른 데이터
                #-----------------------------------------------------------#
                ### (1) S에서 batch 샘플하기
                ### 해당 batch에는 n_shot개 만큼의 데이터 
                for k in episode_classes:
                    class_k1 = df[df['class_id'] == k]
                    support = class_k1.sample(self.n_shot)
                    support_k[k] = support
                    for i, s in support.iterrows():
                        id_batches.append(s['id'])
                        
                ### (2) Q에서 batch 샘플하기
                ### 해당 batch에는 num_Q개 만큼의 데이터 
                for k in episode_classes:
                    class_k2=df[(df['class_id'] == k) & (~df['id'].isin(support_k[k]['id']))]
                    query = class_k2.sample(self.num_Q)
                    for i, q in query.iterrows():
                        id_batches.append(q['id'])
            yield np.stack(id_batches)

2. Sub modules

(1) Flatten

• 3d의 input image를 1차원으로 flatten 시키는 함수

class Flatten(nn.Module):
    def forward(self, input):
        return input.view(input.size(0), -1)

(2) Conv Block

• “Convolution layer & Batch Normalization & ReLU & Max Pooling”의 과정을 거치는 함수

def conv_block(in_,out_):
    return nn.Sequential(
        nn.Conv2d(in_, out_, 3, padding=1),
        nn.BatchNorm2d(out_),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2)
    )

(3) get_few_shot_encoder

def get_few_shot_encoder(num_input_channels=1):
    return nn.Sequential(
        conv_block(num_input_channels, 64),
        conv_block(64, 64),
        conv_block(64, 64),
        conv_block(64, 64),
        Flatten(),
    )

3. Models

• 보다 복잡한 “full context embedding” 상황 하에서

(1) Embedding function of \(S\) : \(g\)

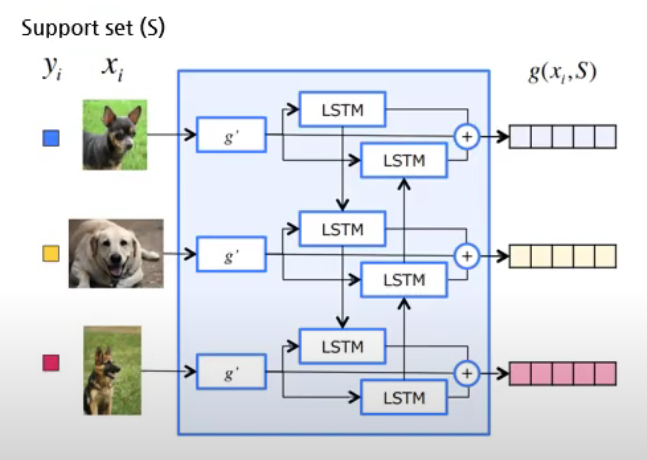
class BidrectionalLSTM(nn.Module):
    def __init__(self, input_dim, num_layers):
        super(BidrectionalLSTM, self).__init__()
        self.num_layers = num_layers
        self.batch_size = 1
        self.lstm = nn.LSTM(input_size=input_dim,
                            num_layers=num_layers,
                            hidden_size=input_dim,
                            bidirectional=True)

    def forward(self, S):
        output,(h, c) = self.lstm(S, None)
        # (1) LEFT
        output_forw = output[:, :, :self.lstm.hidden_size]
        # (2) RIGHT
        output_back = output[:, :, self.lstm.hidden_size:]
        # [FINAL] LEFT + RIGHT + main
        output_concat = output_forw + output_back + S
        return output_concat, h, c

(2) Embedding function of \(Q\) : \(f\)

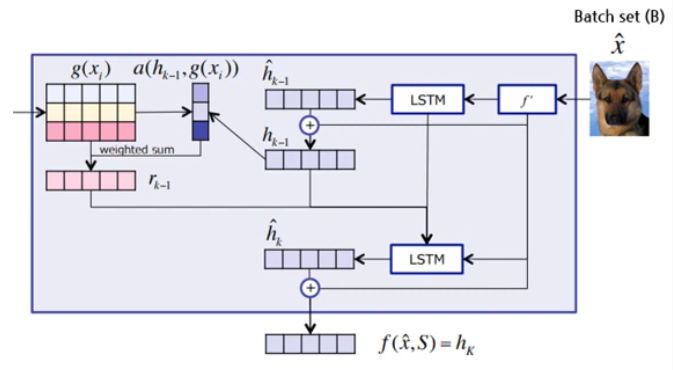
class AttentionLSTM(nn.Module):
    def __init__(self,input_dim, unrolling_steps):
        super(AttentionLSTM, self).__init__()
        self.unrolling_steps = unrolling_steps
        self.lstm_cell = nn.LSTMCell(input_size=input_dim,
                                     hidden_size=input_dim)

    def forward(self, S, Q):
        batch_size = Q.shape[0] # Q의 개수 (= num_Q)
        embedding_dim = Q.shape[1] # Q의 차원
        h = torch.zeros_like(Q).cuda().double() # (num_Q x 1)
        c = torch.zeros(batch_size, embedding_dim).cuda().double() # (num_Q x dim)

        for k in range(self.unrolling_steps):
            #---------------------------------------------
            # (1) hidden state ( cumulative sum )
            # Query set에 계속해서 hidden state를 더한다
            # Hidden state의 변화 : Q -> Q+h1 -> Q+h1+h2 -> ... Q+h1+..+hk
            h_ = h + Q 
            #---------------------------------------------
            # (2) attention ( hidden state & embed(S) )
            # 누적의 Hidden state & Support set의 attention
            att = torch.mm(h_, S.t()).softmax(dim=1)
		    #---------------------------------------------
            # (3) readout
            # Support set x Attention
            readout = torch.mm(att, S)
            #---------------------------------------------
            # (4) run LSTM
            # Input : Query set
            # Hidden : 누적의 Hiddenstate + readout
            # Cell : c
            h, c = self.lstm_cell(Q, (h_ + readout, c))
            
        # 최종 Output : hidden + Query set
        H = h + Q
        return H

(3) Matching Network (MN)

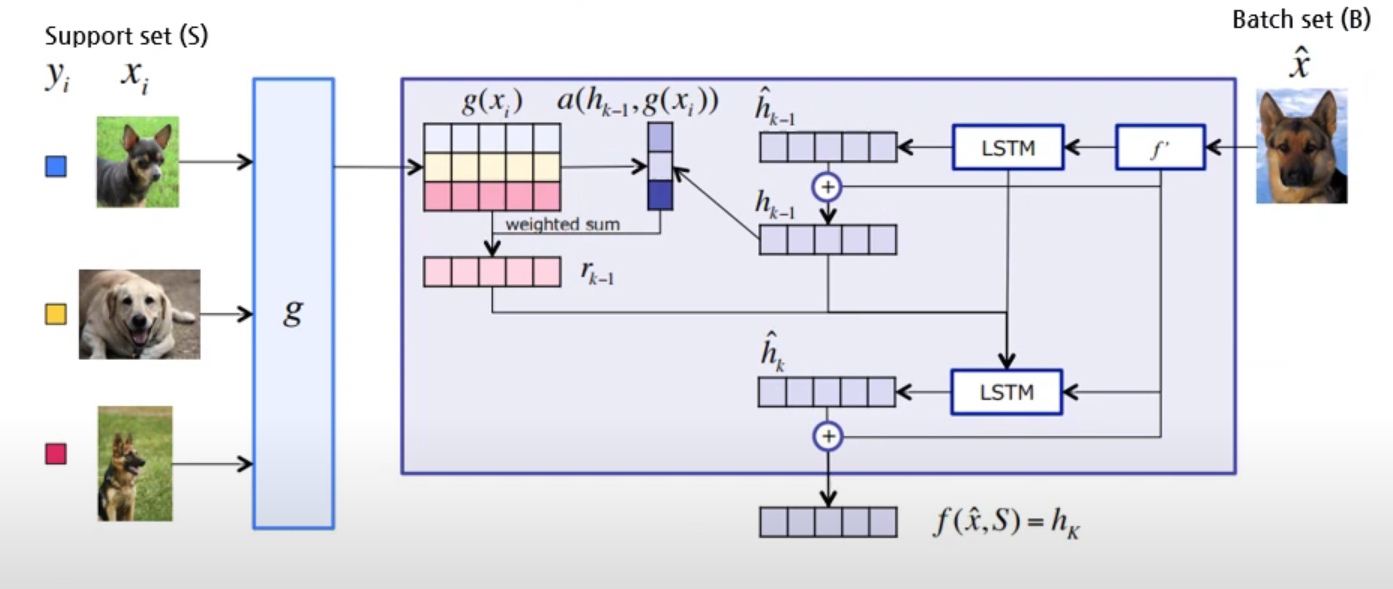
class MatchingNet(nn.Module):
    def __init__(self, n_shot,k_way,num_Q,full_context, num_input_channels,
                 lstm_layers, lstm_input_dim, unrolling_steps, device):
        super(MatchingNet, self).__init__()
        self.n_shot = n_shot
        self.k_way = k_way
        self.num_Q = num_Q
        self.full_context = full_context
        self.num_input_channels = num_input_channels
        self.encoder = get_few_shot_encoder(self.num_input_channels)
        if self.full_context:
            # (1) g ( for S 임베딩 )
            self.g = BidrectionalLSTM(lstm_input_dim, lstm_layers).to(device, dtype=torch.double)
            # (2) f ( for Q 임베딩 )
            self.f = AttentionLSTM(lstm_input_dim, unrolling_steps=unrolling_steps).to(device, dtype=torch.double)

    def forward(self, inputs):
        pass

4. Training

(1) One Step GD

하나의 batch에 대해

• (1) prediction
• (2) loss 계산
• (3) back-prop

def gradient_step(model, opt, loss_fn, x, y, **kwargs):
    model.train()
    opt.zero_grad()
    y_pred = model(x)
    loss = loss_fn(y_pred, y)
    loss.backward()
    opt.step()
    return loss, y_pred

(2) One Episode

def matching_net_epsiode(model,opt,loss_fn,X,y,n_shot,k_way,num_Q,dist_func,full_context,train):
    #---------------------------------------------
    # (1) Settings ( Train or Test )
    if train:
        model.train()
        opt.zero_grad()
    else:
        model.eval()
        
    #---------------------------------------------
    # (2) Embed inputs
    ## "COMMON" embedding for all input ( before getting into f/g function )
    Emb = model.encoder(x)
    
    #---------------------------------------------
    # (3) Divide input into S(support) & Q(query)
    S = Emb[:n_shot * k_way]
    Q = Emb[n_shot * k_way:]    
    
    #---------------------------------------------
    # [Optional] Full Context Embedding
    ## embed, considering support set (S)
    ## g : biLSTM
    ## f : attLSTM
    if full_context:
        S, _, _ = model.g(S.unsqueeze(1))
        S = S.squeeze(1)
        Q = model.f(S, Q)
        
    #---------------------------------------------
    # (4) distance between (1) Q & (2) S
    # ( 여기서 f(Q), g(S) 계산 시 context(S) 고려 X )
    dist = pairwise_distances(Q, S, dist_func)
    att_dist = (-dist).softmax(dim=1)
    
    #---------------------------------------------
    # (5) Prediction
    y_pred = MN_predict(att_dist, n_shot, k_way, num_Q)
    
    #---------------------------------------------
    # (6) Loss (NLL)
    # Clip predictions ( for numerical stability )
    y_pred = y_pred.clamp(EPSILON, 1 - EPSILON)
    loss = loss_fn(y_pred.log(), y)
    
    #---------------------------------------------
    # (7) Back Propagation
    if train:
        loss.backward()
        clip_grad_norm_(model.parameters(), 1)
        opt.step()
    
    return loss, y_pred

5. Prediction

ex) (k_way =) 3 class, with (n_shot =) 5 data per each class

• [0],[0],[0],[0],[0],[1],[1],[1],[1],[1],[2],[2],[2],[2],[2],

def k_n_labels(k_way, n_shot):
    y = torch.arange(0, k_way, 1 / n_shot).long()
    return y.unsqueeze(-1)

\(\begin{aligned} &P\left(\hat{y}_{k}=1 \mid \hat{x}, \delta\right)=\sum_{i=1}^{k} a\left(\hat{x}, x_{i}\right) y_{i} \\ &a(\hat{x}, x)=\frac{\exp (c(f(\hat{x}), g(x)))}{\sum_{i=1}^{K} \exp \left(c\left(f(\hat{x}), g\left(x_{i}\right)\right)\right)} \end{aligned}\).

def MN_predict(att_dist,n_shot,k_way,num_Q):
    if att_dist.shape != (num_Q * k_way, k_way * n_shot):
        raise(ValueError(f'Attention matrix shape error! Should be (q * k, k * n) = ({q * k, k * n})'))
    label_mask = k_n_labels(k_way, n_shot)
    y_onehot = torch.zeros(k_way * n_shot, k_way)
    y_onehot = y_onehot.scatter(1, label_mask, 1)
    y_pred = torch.mm(att_dist, y_onehot.cuda().double())
    return y_pred