Meta Learning Probabilistic Inference For Prediction
Contents
- Abstract
- Introduction
- ML-PIP
- multi-task PROBABILISTIC MODEL
- Probabilistic Inference
- Versatile Amortized Inference
0. Abstract
data efficient & versatile learning 방법(framework)을 제안함
두 가지 framework
- 1) ML-PIP : Meta-Learning approximate Probabilistic Inference for Prediction
- 2) VERSA : flexible & versatile amortization network
- input : few-shot learning dataset
- output : distn over task-specific params
* Amortized Inference
- \(x_i\)를 input으로 받아서 \(z_i\)를 만들어내도록 하는 방법
1. Introduction
Few-shot learning
- data efficiency가 중요 ( 데이터가 적으니까 )
- HOW? by 관련된 task들 사이의 “information sharing”
ML-PIP
-
Meta-Learning approximate Probabilistic Inference for Prediction
-
amortizing posterior predictive distn
-
ML-PIP는 “기존의 point-estimate” probabilistic interpretations을 확장시킴!
-
-
이 framework는 3가지 핵심 요소를 가진다
- 1) task들 사이의 SHARED statistical structure를 가짐
- via HIERARCHICAL probabilistic models & transfer learning
- 2) task들 사이의 information을 SHARE
- 3) FAST learning ( via amortization )
- 1) task들 사이의 SHARED statistical structure를 가짐
VERSA
- test time에 수행하는 optimization 과정을 forward pass로 대체함
2. ML-PIP
ML-PIP framework는 2가지로 구성된다
- 1) multi-task probabilistic model
- 2) method for meta-learning probabilistic inference
2-1. multi-task PROBABILISTIC MODEL
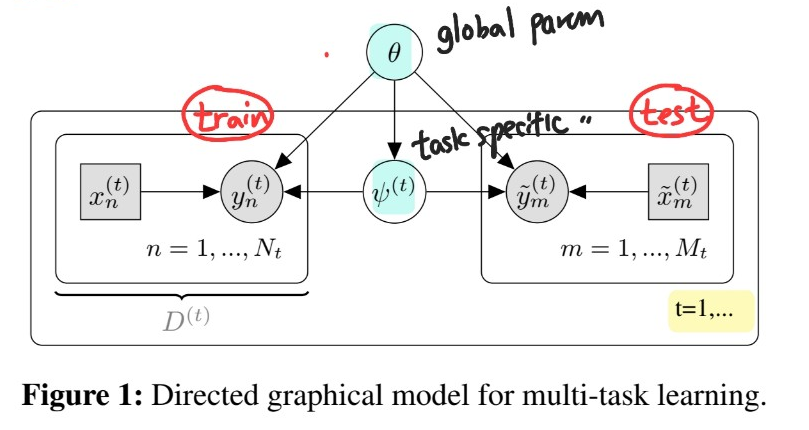
Notation
-
task : \(t\)
- Training data : \(D^{(t)}=\left\{\left(x_{n}^{(t)}, y_{n}^{(t)}\right)\right\}_{n=1}^{N_{t}}\)
- Test Data : \(\left\{\left(\tilde{x}_{m}^{(t)}, \tilde{y}_{m}^{(t)}\right)\right\}_{m=1}^{M_{t}}\)
Model의 선택에 있어서 중요한 2가지
- 1) supervised learning task를 잘 푸는 discriminative model
- 2) task들 사이의 “shared” statistical structure를 가지는 것
위 2가지를 충족한 대표적 ex)
Joint Probability
- [output] outputs \(Y\) & task specific parameters for \(T\) tasks ( \(\psi^{(t)}\) )
- [input] inputs \(X\) & global parameters ( \(\theta\) )
- \(p\left(\left\{Y^{(t)}, \psi^{(t)}\right\}_{t=1}^{T} \mid\left\{X^{(t)}\right\}_{t=1}^{T}, \theta\right)=\prod_{t=1}^{T} p\left(\psi^{(t)} \mid \theta\right) \prod_{n=1}^{N_{t}} p\left(y_{n}^{(t)} \mid x_{n}^{(t)}, \psi^{(t)}, \theta\right) \prod_{m=1}^{M_{t}} p\left(\tilde{y}_{m}^{(t)} \mid \tilde{x}_{m}^{(t)}, \psi^{(t)}, \theta\right)\).
Posterior Predictive distribution
- \(\tilde{x}\) : unseen task의 데이터
-
goal : unseen task에 대해서 fast & accurate approximation하기
- \(p\left(\tilde{y}^{(t)} \mid \tilde{x}^{(t)}, \theta\right)=\int p\left(\tilde{y}^{(t)} \mid \tilde{x}^{(t)}, \psi^{(t)}, \theta\right) p\left(\psi^{(t)} \mid \tilde{x}^{(t)}, D^{(t)}, \theta\right) \mathrm{d} \psi^{(t)}\).
2-2. Probabilistic Inference
- Point estimates for “shared param” ( \(\theta\) )
- Distributional estimates for “task specific param” (\(\psi^{(t)}\))
\(\theta\)를 구하고 난 뒤… 2가지 step으로 구성
- step 1) form posterior distn : \(p\left(\psi^{(t)} \mid \tilde{x}^{(t)}, D^{(t)}, \theta\right)\)
- step 2) compute posterior predictive distn (p.p.d) : \(p\left(\tilde{y}^{(t)} \mid \tilde{x}^{(t)}, \theta\right)\)
Specification of approximate p.p.d
-
amortized distn을 사용하여 근사한다 … \(q_{\phi}(\tilde{y} \mid D) \approx p\left(\tilde{y}^{(t)} \mid \tilde{x}^{(t)}, \theta\right)\).
-
\(q_{\phi}(\tilde{y} \mid D)=\int p(\tilde{y} \mid \psi) q_{\phi}(\psi \mid D) \mathrm{d} \psi\).
- MC sampling 필요!
- factorized Gaussian distn 사용할 것
Meta-learning the approximate p.p.d
- minimize \(\mathrm{KL}\left[p(\tilde{y} \mid D) \mid \mid q_{\phi}(\tilde{y} \mid D)\right]\)
- goal of learning :
- \(\phi^{*}=\underset{\phi}{\arg \min } \underset{p(D)}{\mathbb{E}}\left[\operatorname{KL}\left[p(\tilde{y} \mid D) \mid \mid q_{\phi}(\tilde{y} \mid D)\right]\right]=\underset{\phi}{\arg \max } \underset{p(\tilde{y}, D)}{\mathbb{E}}\left[\log \int p(\tilde{y} \mid \psi) q_{\phi}(\psi \mid D) \mathrm{d} \psi\right]\).
- Training Procedure
- step 1) task \(t\)를 random sample
- step 2) task \(t\)에 해당하는 training data \(D^{(t)}\) random sample
- step 3) posterior predictive \(q_{\phi}\left(\cdot \mid D^{(t)}\right)\) 세우기
- step 4) test data \(\tilde{y}^{(t)}\) 에서의 log-density 구하기 : \(\log q_{\phi}\left(\tilde{y}^{(t)} \mid D^{(t)}\right)\)
- 특이한 점 : directly p.p.d의 KL을 minimize
- (X) \(\mathrm{KL}\left(q_{\phi}(\psi \mid D) \mid \mid p(\psi \mid D)\right)\)
- (O) \(\mathrm{KL}\left(p(\tilde{y} \mid D) \mid \mid q_{\phi}(\tilde{y} \mid D)\right)\)
End-to-end stochastic training
end-to-end stochastic training의 최종 Loss Function :
\(\hat{\mathcal{L}}(\theta, \phi)=\frac{1}{M T} \sum_{M, T} \log \frac{1}{L} \sum_{l=1}^{L} p\left(\tilde{y}_{m}^{(t)} \mid \tilde{x}_{m}^{(t)}, \psi_{l}^{(t)}, \theta\right), \quad \text { with } \psi_{l}^{(t)} \sim q_{\phi}\left(\psi \mid D^{(t)}, \theta\right)\).
- \(\left\{\tilde{y}_{m}^{(t)}, \tilde{x}_{m}^{(t)}, D^{(t)}\right\} \sim p(\tilde{y}, \tilde{x}, D)\).
- episodic train / test splits at meta-train time
3. Versatile Amortized Inference
versatile system?
- inference를 rapid & flexible하게!
- [ rapid ] test-time inference에 single computation만! ( ex. feed-forward pass )
- [ flexible ] support variety of tasks
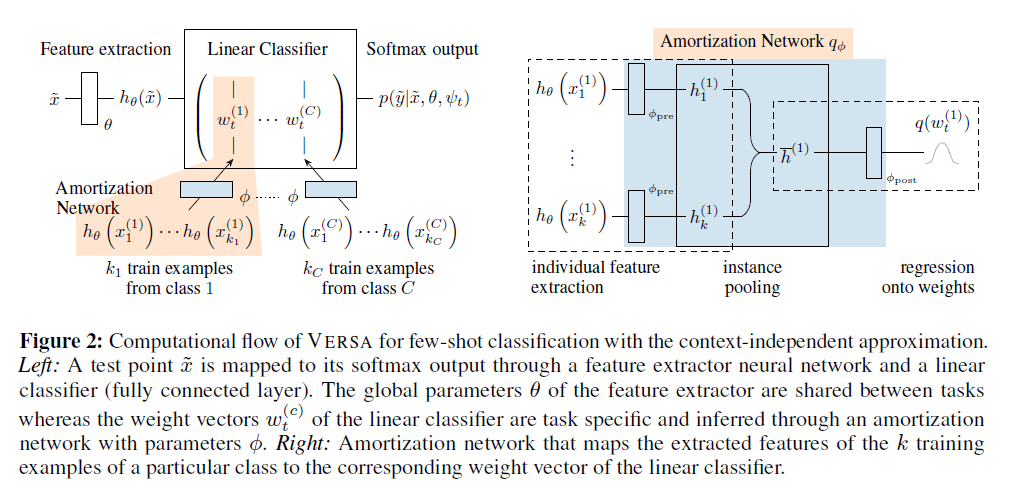
Versa for Few-shot Image Classification
feature extraction NN : \(h_{\theta}(x) \in \mathbb{R}^{d_{\theta}}\)
- shared across all task
- feeds into task-specific linear classifiers … \(\psi^{(t)}=\left\{W^{(t)}, b^{(t)}\right\}\)
posterior \(q_{\phi}(\psi \mid D, \theta)\)를 모델링하는데에 있어서…
- 기존의 Naive amortization : \(C\) ( = number of classes ) 사전 고정
- distribution over \(\mathbb{R}^{d_{\theta} \times C}\)
- 제안한 방법 : \(C\) ( = number of classes ) 사전 고정 X
- context independent 방식
- each weight vector \(\psi_{c}\) ONLY depends on examples from class \(c\)
제안한 posterior 모델링 :
- operates directly on extracted features \(h_{\theta}(x)\)
- \(q_{\phi}(\psi \mid D, \theta)=\prod_{c=1}^{C} q_{\phi}\left(\psi_{c} \mid\left\{h_{\theta}\left(x_{n}^{c}\right)\right\}_{n=1}^{k_{c}}, \theta\right)\).