[meta] (paper 12) Learning to Balance ; Bayesian Meta Learning for Imbalanced and Out-of-distribution Tasks

Learning to Balance : Bayesian Meta Learning for Imbalanced and Out-of-distribution Tasks (2020)

Contents

1. Abstract
2. Introduction
3. Related Work
   1. Meta-Learning
   2. Task-Adaptive Meta-learning
   3. Probabilistic Meta-Learning
4. Learning to Balance

   1. TAML (Task-Adaptive Meta-Learning)

   2. Bayesian TAML

5. Variational Inference

0. Abstract

notation : (A : 현실) & (B :기존 meta-learning 방법론들의 가정)

Problem 1

• (A) tasks come with “VARYING NUMBER” of instances & classes

• (B) number of instance per tasks&classes is “FIXED”

  \(\rightarrow\) learn to “EQUALLY” utilize meta-knowledge across all tasks

Problem 2

• (A) distributional difference in unseen tasks

• (B) DO NOT consider distributional difference in unseen tasks,

  on which the meta-knowledge may have less usefulness depending on the task relatedness

위의 두 문제점을 극복하는 방법 제안

• meta-learning model that “ADAPTIVELY balances” the ffect of

  • (1) meta-learning
  • (2) task-specific learning

  within each task

위 문제를 “Bayesian Inference Framework”를 사용해서 푼다

\(\rightarrow\) Bayesian TAML (Task-Adaptive Meta-Learning)을 제안한다

1. Introduction

It would be beneficial for the model to..

• “task”-adaptively
• “class”-adatively

decide how much to…

• use from the meta-learner
• learn specifically for each task & class

Bayesian TAML

learns variables to “ADAPTIVELY” balance the effect of (1) meta and (2) task specific learning

[ Step 1 ] obtain “set-representations” for each task

[ Step 2 ] learn the distribution of 3 balancing variables

• 1) task-dependent learning rate multiplier
  • meta-knowledge로부터 얼마나 멀리 deviate할지 결정
• 2) class-dependent learning rate
  • 각 class로부터 얼마나 information을 이용할지
• 3) task-dependent modulator for initial model parameter
  • modifies the shared initialization for each task

Contribution

1. realistic task distribution을 가정하여 문제를 품
   1. number of instances across classes & tasks could largely vary
   2. unseen task is different from seen task
2. Bayesian TAML을 제안함

2. Related Work

2-1. Meta Learning

model to “GENERALIZE” over a “DISTRIBUTION of TASK”

• memory-based
• metric-based
• optimization-based

effective learning을 위해, “Episodic Training Strategy”를 사용하는 경우가 많음

• train
  • meta-train
  • meta-test
• test

2-2. Task-Adaptive Meta-learning

하나의 meta-learner만으로 모든 task잘푸는건 너무 오바!

( lead to suboptimal performances for each task )

따라서, “TASK-ADAPTIVELY” modified meta-learning models 사용

• ex 1) temperature scaling parameter ( to work with the optimal similarity metric )
• ex 2) task specific params
  • BUT, only trains with many-shot classes
  • implicitly expects generalization to few-shot cases
• ex 3) network type task-specific parameter producer

이 논문에서 제안한 방법론 또한 “task-specific parameter”를 사용하긴 하지만,

보다 초점은 “HOW TO BALANCE” between meta-learning & task/class-specific learning

2-3. Probabilistic Meta-Learning

probabilistic version of MAML

• V.I framework 사용

Bayesian MAML

• Stein V.I & chaser loss

Probabilistic Meta-Learning framework

위의 세 방법론들 : to represent the inherent UNCERTAINTY in few-shot classification tasks

이 논문에서 제안한 모델도, 마찬가지로 “Bayesian Modeling”을 사용함!

하지만 주요 focus는 BALANCING!

3. Learning to Balance

MAML 복습

Notation

• task distribution : \(p(\tau)\)
• training set : \(\mathcal{D}^{\tau}=\left\{\mathbf{X}^{\tau}, \mathbf{Y}^{\tau}\right\}\)

• test set : \(\tilde{\mathcal{D}}^{\tau}=\left\{\tilde{\mathbf{X}}^{\tau}, \tilde{\mathbf{Y}}^{\tau}\right\}\)

• initial model parameter : \(\theta\)

Goal of MAML :

meta-learn the initial model parameter \(\theta\) as a meta-knowledge to generalize over the task distribution \(p(\tau)\), such that we can easily obtain the task-specific predictor \(\theta^{\tau}\) in a single (or a few) gradient step from the initial \(\theta\).

• objective function : \(\min _{\boldsymbol{\theta}} \sum_{\tau \sim p(\tau)} \mathcal{L}\left(\boldsymbol{\theta}-\alpha \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta} ; \mathcal{D}^{\tau}\right) ; \tilde{\mathcal{D}}^{\tau}\right)\)
• task=specific parameter : \(\boldsymbol{\theta}^{\tau}=\boldsymbol{\theta}-\alpha \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta} ; \mathcal{D}^{\tau}\right)\)

MAML의 문제점

1. Class Imbalance
2. Task Imbalance
3. Out-of-distribution tasks

3-1. TAML (Task-Adaptive Meta-Learning)

3개의 balancing variables를 도입한다

• \(\omega^{\tau}, \gamma^{\tau}, \mathbf{z}^{\tau}\).

(1) Class Imbalance 해결 ( by \(\omega^{\tau}\) )

• vary the learning rate of class-specific gradient
• class specific scalars \(\boldsymbol{\omega}^{\tau}=\left(\omega_{1}^{\tau}, \ldots, \omega_{C}^{\tau}\right) \in[0,1]^{C}\) 도입
  • class specific gradients \(\nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta} ; \mathcal{D}_{1}^{\tau}\right), \ldots, \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta} ; \mathcal{D}_{C}^{\tau}\right)\) 에 곱해짐

(2) Task Imbalance 해결 ( by \(\gamma^{\tau}\) )

• control whether model param for current task “stay close/far” from initial param
• task-dependent learning-rate multipliers \(\gamma^{\tau}=\left(\gamma_{1}^{\tau}, \ldots, \gamma_{L}^{\tau}\right) \in[0, \infty)^{L}\) 도입
  • \(\gamma_{1}^{\tau} \alpha, \gamma_{2}^{\tau} \alpha, \ldots, \gamma_{L}^{\tau} \alpha^{1}\).
  • large task에 대해 \(\gamma^{\tau}\)가 크기를 ( meta-knowledge 적게 활용해 )
  • small task에 대해서 \(\gamma^{\tau}\)가 작기를 ( meta-knowledge 많이 활용해 )

(3) Out-of-distribution 해결 ( by \(\mathbf{z}^{\tau}\) )

• modulate the initial parameter \(\theta\) for each task
• \(\mathbf{z}^{\tau}\) 가 initial parameter 자체를 relocate시키는 역할
• weight) \(\theta_{0} \leftarrow \theta \circ \mathbf{z}^{\tau}\)
• bias) \(\theta_{0} \leftarrow \theta+\mathbf{z}^{\tau}\)

Unified Framework

위의 (1)~(3) 요소 전부 사용

\(\begin{aligned} \boldsymbol{\theta}_{0} &=\boldsymbol{\theta} * \mathbf{z}^{\tau} \\ \boldsymbol{\theta}_{k} &=\boldsymbol{\theta}_{k-1}-\gamma^{\tau} \circ \boldsymbol{\alpha} \circ \sum_{c=1}^{C} \omega_{c}^{\tau} \nabla_{\boldsymbol{\theta}_{k-1}} \mathcal{L}\left(\boldsymbol{\theta}_{k-1} ; \mathcal{D}_{c}^{\tau}\right) \quad \text { for } k=1, \ldots, K \end{aligned}\).

• \(\alpha\) : multi-dimensional global learning rate
• last step \(\theta_k\) : task-specific parameter \(\theta^{\tau}\)

3-2. Bayesian TAML

VI framework 도입

Notation

• training set : $\mathbf{X}^{\tau}=\left{\mathbf{x}{n}^{\tau}\right}{n=1}^{N_{\tau}}$ & $\mathbf{Y}^{\tau}=\left{\mathbf{y}{n}^{\tau}\right}{n=1}^{N_{\tau}}$

• testing set : $\tilde{\mathbf{X}}^{\tau}=\left{\tilde{\mathbf{x}}{m}^{\tau}\right}{m=1}^{M_{\tau}}$ & $\tilde{\mathbf{Y}}^{\tau}= \left{\tilde{\mathbf{y}}{m}^{\tau}\right}{m=1}^{M_{\tau}}$

• $\phi^{\tau}$ : collection of $\tilde{\boldsymbol{\omega}}^{\tau}, \tilde{\gamma}^{\tau}$ and $\tilde{\mathbf{z}}^{\tau}$

Generative Process for Meta-learning framework ( for task $\tau$ )

• $p\left(\mathbf{Y}^{\tau}, \tilde{\mathbf{Y}}^{\tau}, \phi^{\tau} \mid \mathbf{X}^{\tau}, \tilde{\mathbf{X}}^{\tau} ; \boldsymbol{\theta}\right)=p\left(\phi^{\tau}\right) \prod_{n=1}^{N_{\tau}} p\left(\mathbf{y}{n}^{\tau} \mid \mathbf{x}{n}^{\tau}, \phi^{\tau} ; \boldsymbol{\theta}\right) \prod_{m=1}^{M_{\tau}} p\left(\tilde{\mathbf{y}}{m}^{\tau} \mid \tilde{\mathbf{x}}{m}^{\tau}, \phi^{\tau} ; \boldsymbol{\theta}\right)$.

4. Variational Inference

True posterior $p(\phi^{\tau} \mid \mathcal{D}^{\tau}, \tilde{\mathcal{D}^{\tau}})$ is intractable!

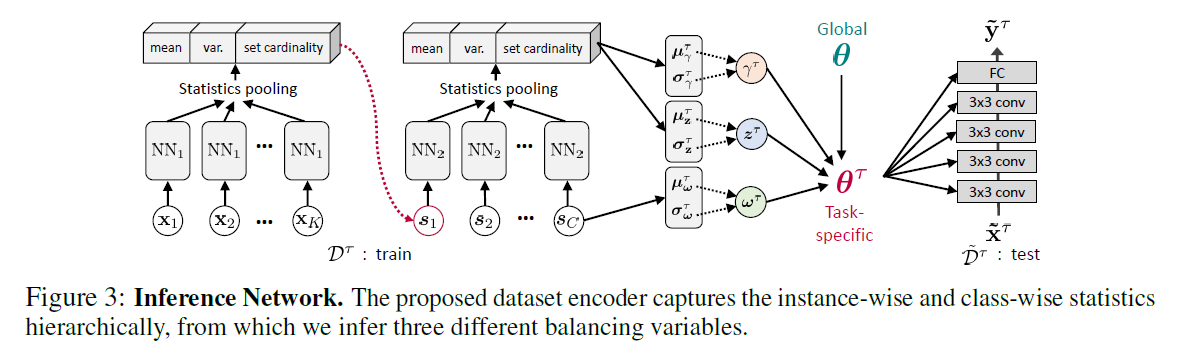
4-1. Dataset Encoding

how to refine $\mathcal{D}^{\tau}$ into