[meta] (paper 9) Meta-Weight-Net ; Learning an Explicit Mapping For Sampling Weighting

Meta-Weight-Net : Learning an Explicit Mapping For Sampling Weighting

Contents

1. Abstract
2. Introduction
3. The Proposed Meta-Weight-Net Learning Method
   1. Meta Learning Objective
   2. MW-Net learning method
   3. Algorithm

0. Abstract

DNN : biased training data에 overfit 우려!

\(\rightarrow\) 자주 사용되는 해결책 : re-weighting strategy

Re-weighting strategy

• 1) mapping from “training loss” to “sample weight”
• 2) iterate between “weight recalculating” & “classifier updating”

Recent Approaches

need to manually PRE-specify the …

• 1) weighting function

• 2) hyperparameters

Proposal

method capable of ADAPTIVELY learning an

EXPLICIT weighting function directly from DATA

( = use MLP with one hidden layer )

1. Introduction

Sampling re-weighting approach

2개의 contradictive ideas for constructing loss-weight mapping

[ 방법 1 ] monotonically INCREASING

• 크게 틀릴수록 weight \(\uparrow\)
• ex) AdaBoost, hard negative mining, focal loss

[ 방법 2 ] monotonically DECREASING

• 작게 틀릴수록 weight \(\uparrow\)
• ex) self-paced learning(SPL), iterative reweighting

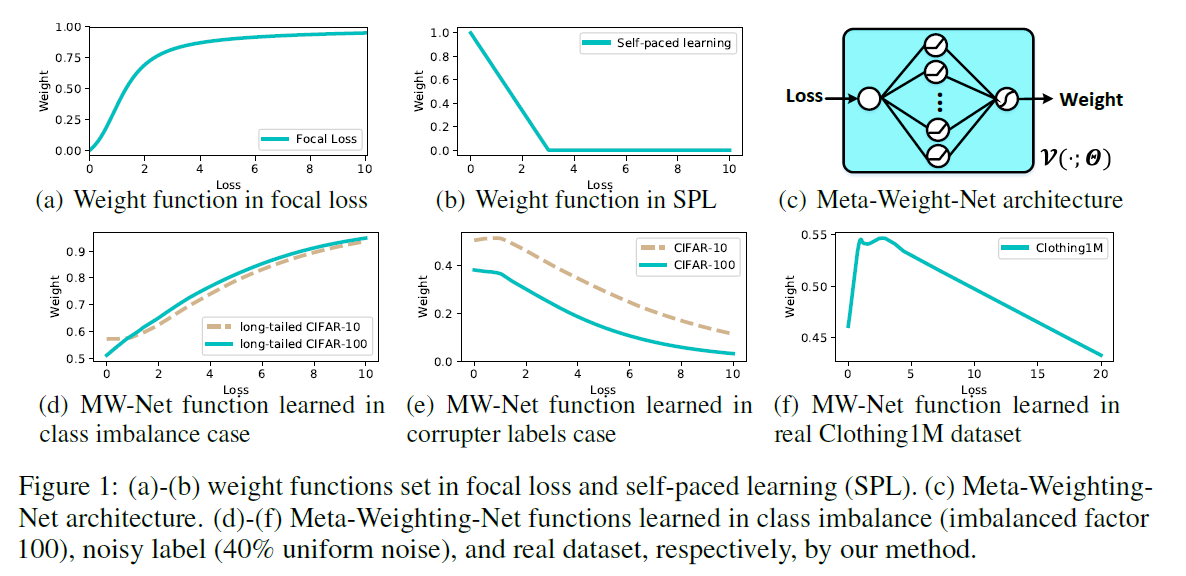
Problems with 기존 방법들

(1) need to manually set a specific form of weighting function, based on certain assumptions o training data

\(\rightarrow\) underlying data에 대해 little knowledge 밖에 없는 현 상황상 infeasible

(2) hyper-parameter 또한 정해야

Proposal

“Adaptive” sampling weighting strategy

• automatically learn “explicit weighting function” from data
• main idea : parameterize the weighting function as MLP
• propose “META-WEIGHT-NET”

2. The Proposed Meta-Weight-Net Learning Method

2-1. Meta-learning objective

Notation

• training set : \(\left\{x_{i}, y_{i}\right\}_{i=1}^{N}\)
• label vector over \(c\) classes : \(y_{i} \in\{0,1\}^{c}\)

• \(f(x, \mathbf{w})\) : classifier ( = DNN )

• loss function : \(L_{i}^{\text {train }}(\mathbf{w})=\frac{1}{N} \sum_{i=1}^{N}\ell\left(y_{i}, f\left(x_{i}, \mathrm{w}\right)\right)=\ell\left(y_{i}, f\left(x_{i}, \mathbf{w}\right)\right)\)(for simplicity)

WEIGHTED loss :

• \(\mathbf{w}^{*}(\Theta)=\underset{\mathbf{w}}{\arg \min } \mathcal{L}^{\text {train }}(\mathbf{w} ; \Theta) \triangleq \frac{1}{N} \sum_{i=1}^{N} \mathcal{V}\left(L_{i}^{\text {train }}(\mathbf{w}) ; \Theta\right) L_{i}^{\text {train }}(\mathbf{w})\).

Meta-Weight-Net (MW-Net)

\(\mathcal{V}\left(L_{i}(\mathbf{w}) ; \Theta\right)\) ,

• MLP with one hidden layer ( 100 nodes )
• ReLU, 마지막엔 Sigmoid

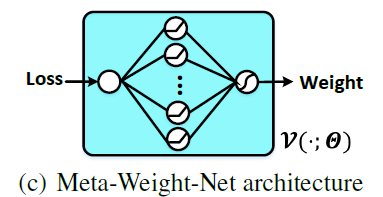
Meta learning process

MW-Net에 있는 parameter들은 \(M\) 개의 meta data ( \(\left\{x_{i}^{(m e t a)}, y_{i}^{(m e t a)}\right\}_{i=1}^{M}\) ) 를 사용해서 학습

• \(\Theta^{*}=\underset{\Theta}{\arg \min } \mathcal{L}^{\operatorname{meta}}\left(\mathbf{w}^{*}(\Theta)\right) \triangleq \frac{1}{M} \sum_{i=1}^{M} L_{i}^{m e t a}\left(\mathbf{w}^{*}(\Theta)\right)\).

2-2. MW-Net learning method

optimal \(\Theta^{*}\) 와 \(\mathbf{w}^{*}\)는 2개의 nested loops of optimization으로 계산한다.

(1) Classifier Learning function ( eq 3)

• \(\hat{\mathbf{w}}^{(t)}(\Theta)=\mathbf{w}^{(t)}-\alpha \frac{1}{n} \times \sum_{i=1}^{n} \mathcal{V}\left(L_{i}^{t r a i n}\left(\mathbf{w}^{(t)}\right) ; \Theta\right) \nabla_{\mathbf{w}} L_{i}^{t r a i n}(\mathbf{w}) \mid _{\mathbf{w}^{(t)}}\).

(2) Update parameters of MW-Net ( w.r.t \(\Theta^{*}\) ) ( eq 4)

• \(\Theta^{(t+1)}=\Theta^{(t)}- \beta \frac{1}{m} \sum_{i=1}^{m} \nabla_{\Theta} L_{i}^{m e t a}\left(\hat{\mathbf{w}}^{(t)}(\Theta)\right) \mid _{\Theta^{(t)}}\).

(3) Update parameters of classifier ( w.r.t \(\mathbf{w}^{*}\) ) ( eq 5)

• \(\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}-\alpha \frac{1}{n} \times \sum_{i=1}^{n} \mathcal{V}\left(L_{i}^{t r a i n}\left(\mathbf{w}^{(t)}\right) ; \Theta^{(t+1)}\right) \nabla_{\mathbf{w}} L_{i}^{t r a i n}(\mathbf{w}) \mid _{\mathbf{w}^{(t)}}\).

2-3. Algorithm