Meta Learning
Meta Learning에 대해 간단히 소개하는 글
Contents
목차
- Introduction
- Meta Learning Problem
- Approaches
- Metric-Based
- Model-Based
- Optimization-Based
1. Introduction
Meta learning?
- learning to learning
- 몇몇의 training task들을 통해서, 새로운 task를 빠르게 풀수 있도록 하기 위해!
- DL의 경우, 데이터 수에 비례한 성능! 데이터 수 적은 경우에 사용하기 적절!
- 크게 3가지 접근 방식
- 1) efficient distance metric 학습
- 2) external/internal memory를 통한 network 사용
- 3) fast learning을 위한 model parameter optimization
Meta Learning model
-
학습하는 동안 접하지 않은 새로운 task에도 잘 적응(일반화)하는 모델
-
좋은 meta learning model이란?
-
task의 다양성에 대해서 학습되어야
-
모든 task ( 기존+신규 task )의 분포 상 최고의 성능을 내도록 최적화
\(\theta^{*}=\arg \min _{\theta} \mathbb{E}_{\mathcal{D} \sim p(\mathcal{D})}\left[\mathcal{L}_{\theta}(\mathcal{D})\right]\).
-
2. Meta Learning Problem
Tasks example)
- Image classification
- Reinforcement Learning
Few Shot Classification
-
Meta Learning + Classification의 예시
-
dataset \(D = <S,B>\)
- \(S\) : Support set … model 학습용
- \(B\) : Batch set … loss 계산 후 optimization용
-
ex) K-shot N-class classification
“K개의 데이터” with “N개의 class”
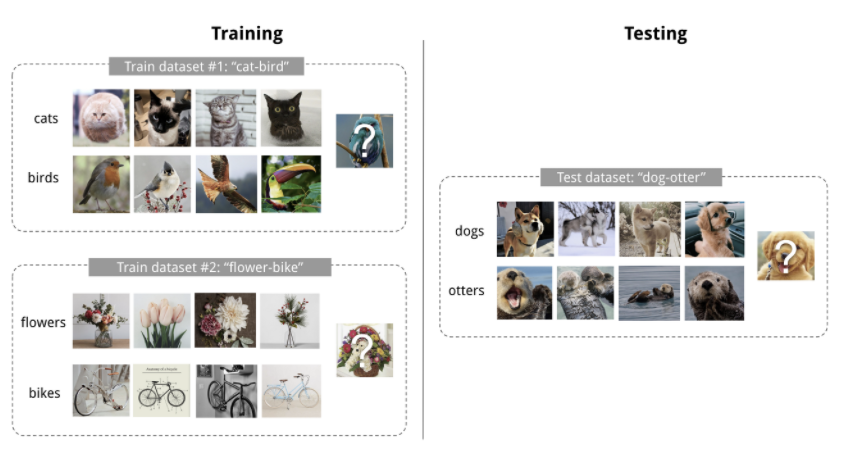
K-shot N-class classification
-
meta learning (X) : \(\theta^{*}=\arg \max _{\theta} \mathbb{E}_{B \subset \mathcal{D}}\left[\sum_{(\mathbf{x}, y) \in B} P_{\theta}(y \mid \mathbf{x})\right]\)
-
meta learning (O) : \(\theta=\arg \max _{\theta} E_{L \subset \mathcal{L}}\left[E_{S^{L} \subset \mathcal{D}, B^{L} \subset \mathcal{D}}\left[\sum_{(x, y) \in B^{L}} P_{\theta}\left(x, y, S^{L}\right)\right]\right]\)
한 줄 요약 : Support set을 사용하여 학습한 뒤, Batch set으로 Loss를 계산하여 이를 minimize하기!
Learner & Meta-Learner
Meta learning은 아래의 [2 step]으로 구성된다고 바라볼 수도 있다.
-
1) Classifier \(f_{\theta}\)
- learner 모델
- 주어진 task를 잘 학습하도록 최적화
-
2) Optimizer \(g_{\phi}\)
- support set \(S\)를 사용하여, 위의 learner model \(f_{\theta}\)의 파라미터 \(\theta\) 를 업데이트
- 업데이트된 파라미터 : \(\theta'=g_{\phi}(\theta, S)\).
-
Final Optimization step :
아래의 식을 최대화하도록 위의 두 classifier & optimzer의 파라미터 \(\theta\)와 \(\phi\)를 업데이트
\(\mathbb{E}_{L \subset \mathcal{L}}\left[\mathbb{E}_{S^{L} \subset \mathcal{D}, B^{L} \subset \mathcal{D}}\left[\sum_{(\mathbf{x}, y) \in B^{L}} P_{g_{\phi}\left(\theta, S^{L}\right)}(y \mid \mathbf{x})\right]\right]\).
3. Approaches
Common Approaches
Meta Learning의 3가지 approaches
- 1) Metric-based
- 2) Model-based
- 3) Optimization-based
3-1. Metric-Based
KDE (Kernel Density Estimation)과 그 개념이 유사하다. 꽤 직관적이다!
\(y\)의 predictied probability = support set sample들의 label의 weighted sum
- weight : 두 sample간의 similarity
- \(P_{\theta}(y \mid \mathbf{x}, S)=\sum_{\left(\mathbf{x}_{i}, y_{i}\right) \in S} k_{\theta}\left(\mathbf{x}, \mathbf{x}_{i}\right) y_{i}\).
Key point : kernel function 잘 학습하기
Example
- Convolutional Siamese NN
- Matching Networks
- Relation Networks
- Prototypical Networks
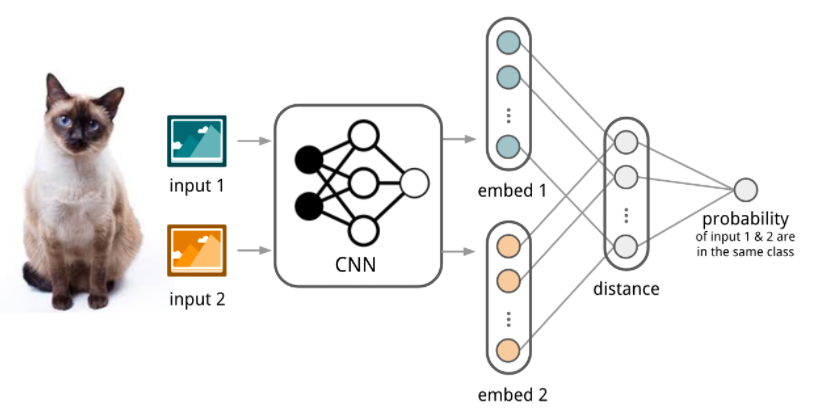
Convolutional Siamese NN
-
Siamese Neural Network for one-shot image recognition
-
(이전) 사람이 설계한 특징으로 learning
(CSNN) 처음으로 NN 사용!
-
CNN을 사용하여 feature extract ( embedding ) & distance 계산
-
직관적 이해
- 다른 class의 사진은 distance가 멀도록
- 같은 class의 사진은 distance가 가깝도록
모델이 학습된다.
Matching Networks
- (논문 리뷰) https://seunghan96.github.io/meta/study/study-(meta)(paper-2)Matching-Networks-for-One-Shot-Learning/
-
(코드 리뷰) https://seunghan96.github.io/meta/study/study-(meta)(code-review)Matching-Network/
-
Convolutional Siamese NN의 한계점?
-
한계점이라기 보다는, test 단계에서 N-way K-shot 문제를 푸는데에 최적화 된 것은 아님!
( Query의 class는 Support Set 중 “상대적”으로 더 유사한(가까운) 것을 찾으면 됨 )
-
따라서, “데이터 간 상대적 거리”를 잘 표현하는 특징 추출기를 만들 필요가 있다
-
-
그래서 사용하는 것이 Attention Kernel
-
\[c_{S}(\mathbf{x})=P(y \mid \mathbf{x}, S)=\sum_{i=1}^{k} a\left(\mathbf{x}, \mathbf{x}_{i}\right) y_{i}, \text { where } S=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{k}\]
where \(a\left(\mathbf{x}, \mathbf{x}_{i}\right)=\frac{\exp \left(\operatorname{cosine}\left(f(\mathbf{x}), g\left(\mathbf{x}_{i}\right)\right)\right.}{\sum_{j=1}^{k} \exp \left(\operatorname{cosine}\left(f(\mathbf{x}), g\left(\mathbf{x}_{j}\right)\right)\right.}\).
-
\[c_{S}(\mathbf{x})=P(y \mid \mathbf{x}, S)=\sum_{i=1}^{k} a\left(\mathbf{x}, \mathbf{x}_{i}\right) y_{i}, \text { where } S=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{k}\]
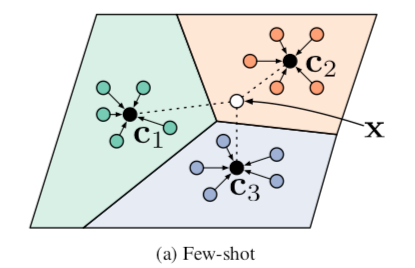
Prototypical Networks
- 프로토타입(prototype) : Class 별 Support set의 평균 위치
- \(\mathbf{v}_{c}=\frac{1}{\mid S_{c} \mid} \sum_{\left(\mathbf{x}_{i}, y_{i}\right) \in S_{c}} f_{\theta}\left(\mathbf{x}_{i}\right)\).
- ex) 4-way 5-shot task :
- 4개 class를 대표하는 Prototype vector & Query vector사이의 거리만 계산
- Query 예측에 필요한 계산량 : N*K \(\rightarrow\) N
- Prediction :
- \(P(y=c \mid \mathbf{x})=\operatorname{softmax}\left(-d_{\varphi}\left(f_{\theta}(\mathbf{x}), \mathbf{v}_{c}\right)\right)=\frac{\exp \left(-d_{\varphi}\left(f_{\theta}(\mathbf{x}), \mathbf{v}_{c}\right)\right)}{\sum_{c^{\prime} \in \mathcal{C}} \exp \left(-d_{\varphi}\left(f_{\theta}(\mathbf{x}), \mathbf{v}_{c^{\prime}}\right)\right)}\).
- 논문에서 사용한..
- distance : 유클리디안
- loss function : Negative-log Likelihood
3-2. Model-Based
\(P_{\theta}(y \mid \mathbf{x})\)에 어떠한 가정도 하지 않음
Example
-
Memory-Augmented Neural Networks (2016)
( 논문 리뷰 : https://seunghan96.github.io/meta/study/study-(meta)(paper-1)-Meta-learning-with-Memory-Augmented-Neural-Networks/ )
-
Meta Networks (2017)
3-3. Optimization-Based
Backpropagation을 통한 학습
But, GD는 small dataset에 부적합할 수 있다 ( converge X )
따라서, 적은 수의 data만으로도 모델을 잘 학습하기 위해서 고안된 것이 바로 “optimization-based approach meta learning”!
Example
-
LSTM Meta-Learner
-
MAML
( 논문 리뷰 : https://seunghan96.github.io/meta/study/study-(meta)(paper-4)Model-Agnostic-Meta-Learning-for-Fast-Adaptation-of-Deep-Networks/ )
-
Reptile
( 논문 리뷰 : https://seunghan96.github.io/meta/study/study-(meta)(paper-6)On-First-Order-Meta-Learning-Algorithms/ )
Reference
-
https://seunghan96.github.io/
- https://talkingaboutme.tistory.com/entry/DL-Meta-Learning-Learning-to-Learn-Fast
- https://lilianweng.github.io/lil-log/2018/11/30/meta-learning.html
