Neural Turing Machine (NMT)
Contents
목차
- Introduction
- 일반적인 NN
- RNN
- Neural Turing Machine (NTM)
- Neural Turing Machine (NTM)
- Read head
- Write head
- Memory 주소 계산 (=Addressing)
1. Introduction
한 줄 요약 : “외부의 memory에 연결 가능한 NN”
( 미분 가능한 version의 Turing Machine )
Neural Network에 대한 관점을, 아래의 그림과 같이 이해해보자.
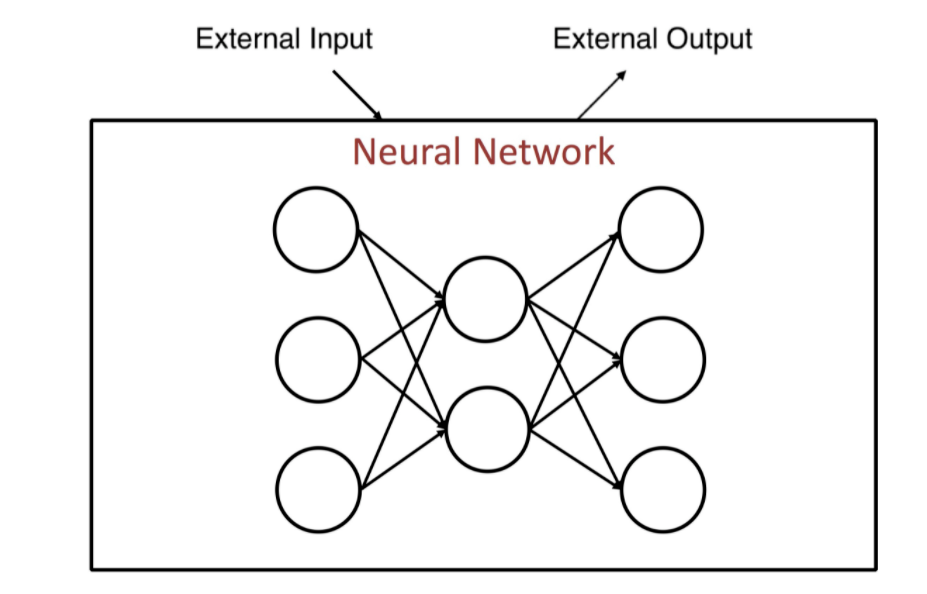
(1) 일반적인 NN
-
input : external input
-
output : external output
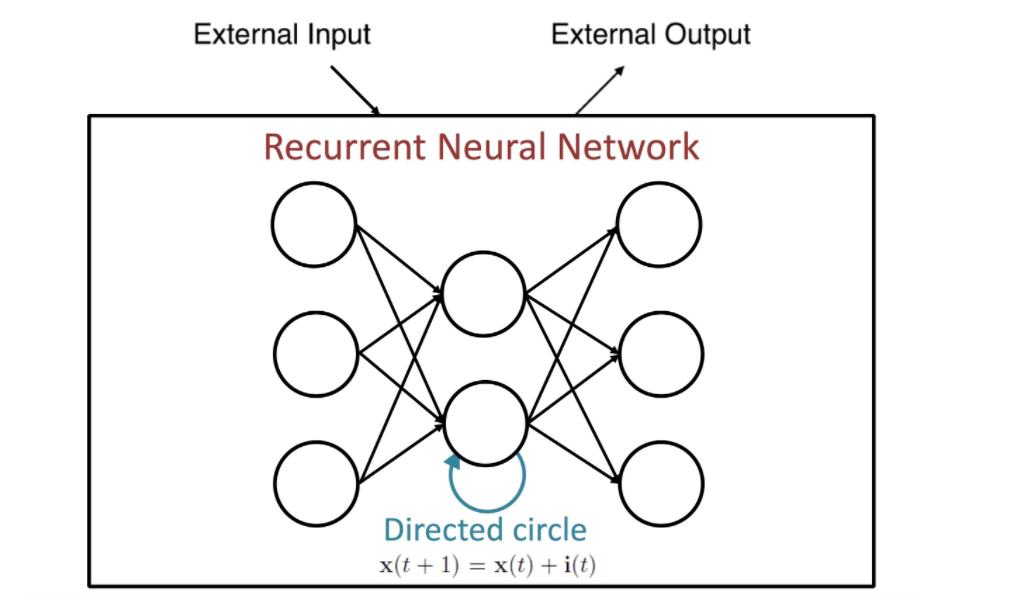
(2) RNN
- input : external input + previous state
- 여기서 previous state는, 일종의 internal memory다
( = 내부의 unit 출력 자체를 다시 input으로 사용 )
- output : external output
(3) Neural Turing Machine (NTM)
위와 같은 관점으로, Neural Turing Machine을 바라보면 아래와 같다.
-
input : external input + EXTERNAL MEMORY
-
output : external output
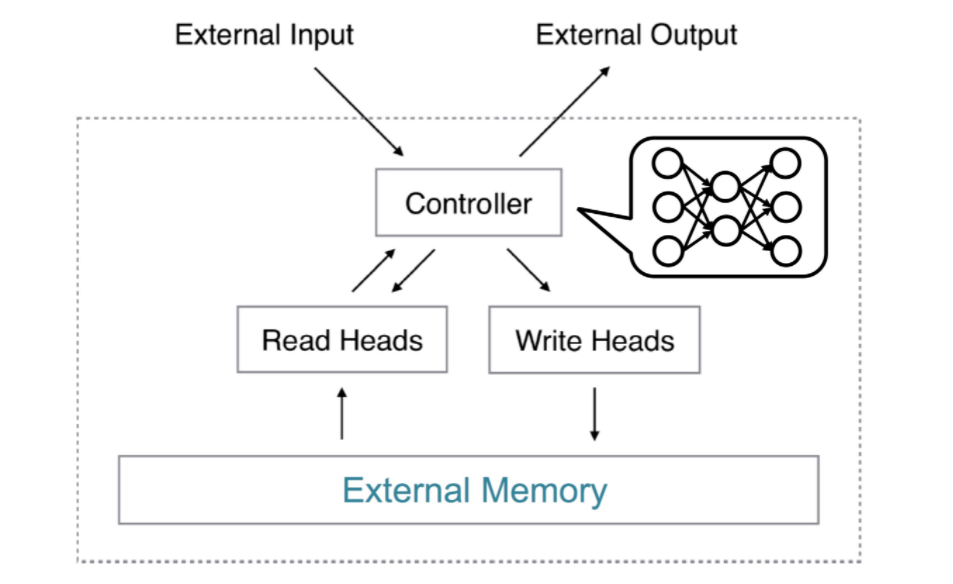
2. Neural Turing Machine (NTM)
위의 그림은, Neural Turing Machine을 도식화 한 것이다.
[ NTM 구조 파헤쳐보기 ]
- Controller : Neural Network 모델
-
READ head를 통해 메모리를 읽고, WRITE head를 통해 메모리를 쓸 수 있음
- 직관적 이해 )
- READ head에서, 다음 output에 도움 될만한 것을 뽑아내고
- WRITE head에서, memory에 현재 정보 추가한다
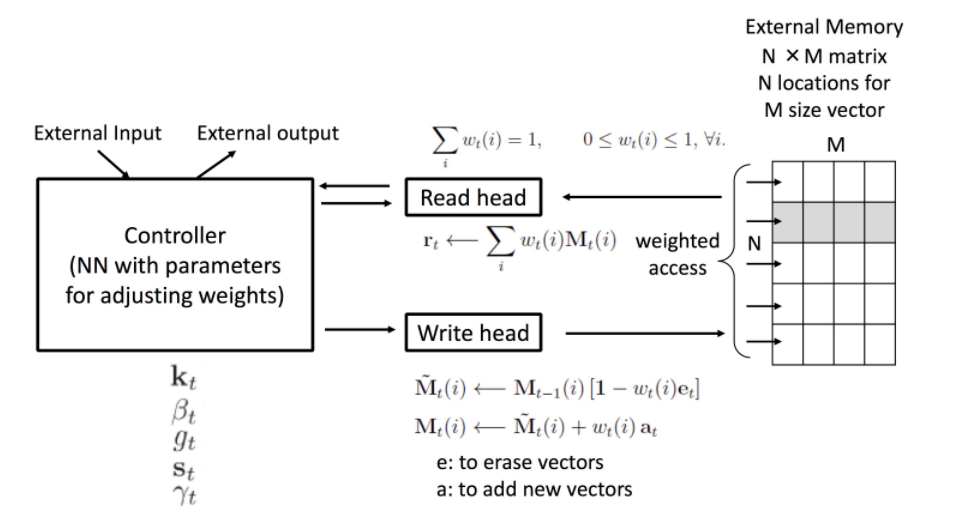
(1) READ head
-
Memory에서 정보 뽑아내는 연산
-
Memory에서 특정 row를 뽑아 내는게 아니라,
여러 row의 linear combination을 뽑아냄 ( = blurry )
-
\(\mathbf{r}_{t} \leftarrow \sum_{i}^{R} w_{t}(i) \mathbf{M}_{t}(i)\).
(2) WRITE head
-
두 가지 process로 진행 ( memory 업데이트 = (1) erase & (2) add )
-
마찬가지로 linear combination
-
과정
-
erase : Memory에서 특정 정보를 지우고 …. \(\tilde{\mathbf{M}}_{t}(i) \leftarrow \mathbf{M}_{t-1}(i)\left[\mathbf{1}-w_{t}(i) \mathbf{e}_{t}\right]\).
-
add : Memory에 특정 정보 추가 …. \(\mathbf{M}_{t}(i) \leftarrow \tilde{\mathbf{M}}_{t}(i)+w_{t}(i) \mathbf{a}_{t}\).
-
위의 (1), (2) 모두 matrix 연산으로써, 미분 가능하다!
(3) Memory 주소 계산 (=Addressing)
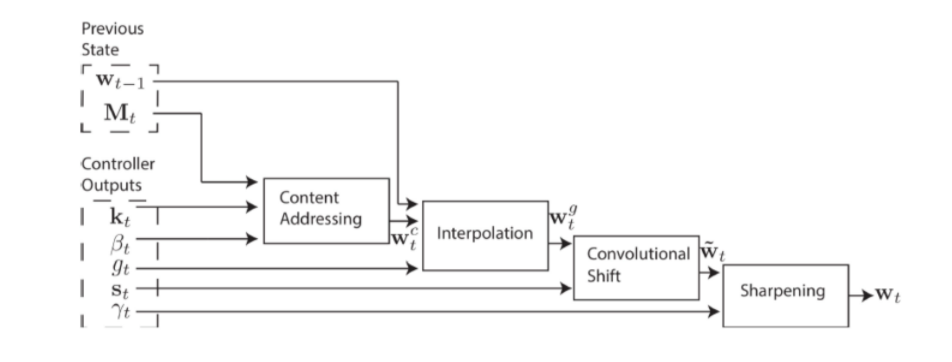
[ Addressing의 2가지 방법 ]
1) content-based addressing : Attention 메커니즘처럼, key vector와의 유사도에 따라 참고하기
2) location-based addressing : location에 따라 찾기
아래의 4가지 step으로 이루어짐
-
1) Content-addressing : key vector \(k_t\)와의 cosine similarity를 통해 content-based weight \(w_t^c\) 계산
- 2) Interpolation
- \(w_t^g\)를 구함…. by \(w_t^c\) & \(w_{t-1}\)의 weighted average
-
3) Convolution Shift : convolution 계산 통해 \tilde{w_t} 얻기
- 4) Sharpening : \(\tilde{w_t}\)를 scaling
Reference
- https://jamiekang.github.io/2017/05/08/neural-turing-machine/
- Neural Turing Machines ( A Graves, 2014 )
