(paper) Context-Guided BERT for Target Aspect-Based Sentiment Analysis (2020)

Context-Guided BERT for Target Aspect-Based Sentiment Analysis (2020)

Contents

1. Abstract
2. Introduction
3. Background and Related Work
   1. Self-attention Networks
   2. Formulation of Quasi-attention
   3. ABSA
   4. TABSA
4. Approach
   1. TABSA task
   2. ABSA Task
   3. Context-Guided Softmax Attention
   4. Context-aware Quasi Attention
   5. Classification
   6. Context Matrix
   7. Integration with Pretrained BERT

0. Abstract

제안한 내용 : “ADD CONTEXT” to self-attention models to solve (T)ABSA

2개의 Context-Guided BERT (CG-BERT)의 variant들을 제안함

( = learn to distribute attention under different CONTEXTS )

• (1) context-guided softmax-attention을 사용하는 CG-BERT

• (2) Quasi-attention CG-BERT

  ( subtractive attention을 반영함 )

1. Introduction

user-generated review는 단지 하나의 감정만을 담고 있지 않다!

\(\rightarrow\) identify the (1) different aspects embedded within a given text & their (2)associated sentiment

이게 곧 ABSA task이다

( TABSA =Targetd ABSA : general version of ABSA … 리뷰 내에 multiple target이 있는 경우! )

이 논문에서는, BERT가 context-aware하도록 improve시킴

( 즉, 다른 context하에서 attention weight를 잘 배분시키기 )

context를 BERT에 반영시키기 위해 2가지의 method를 제안함

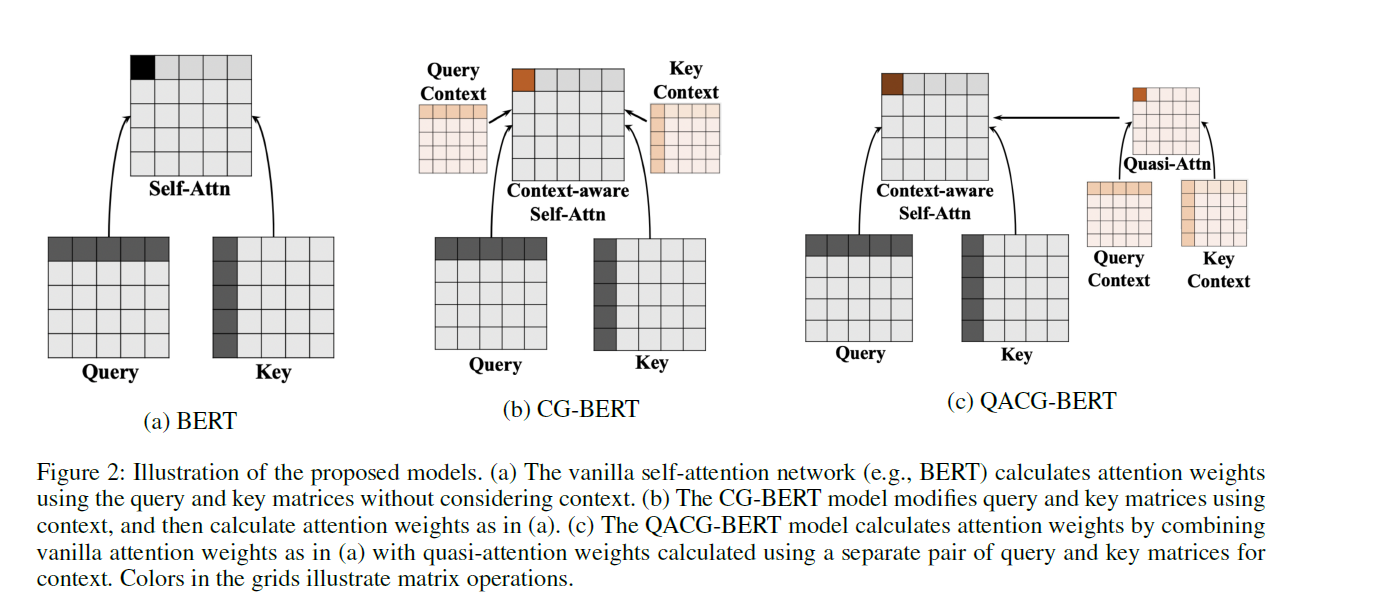
• (1) CG-BERT, adapted from context-aware self attention network
• (2) Quasi-Attention CG-BERT (QACG-BERT)

2. Background and Related Work

2-1) Self-attention Networks

Transformer의 모듈로써도 사용되는 “self-attention”

( Transformer의 encoder 부분을 사용하는 BERT 또한 이 알고리즘 사용 )

[ Self-attention weight의 의미 ]

Self-attention weights may learn ..

• “syntatic” (Hewitt and manning 2019)
• “semantic” (Wu, Nguyen, and Ong 2020) information

2-2) Formulation of Quasi-attention

기존의 Attention weight

• output vector is in the convex hull formed by all other input vectors
• 따라서, subtractive relations를 배울 수 없다!

Tay et al(2019)가 이를 극복하기 위해…

• allowing attention weights to be NEGATIVE ( = quasi-attention )
• (+1) 양의 상관 . (0) 무관 (-1) 음의 상관

2-3) ABSA

최근의 많은 ABSA paper들은 neural models에 ATTENTION을 사용함

가장 최근에는, BERT 많이 사용

( + fine-tuning BERT-based model with an ABSA classification output layer )

2-4) TABSA

TABSA = ABSA + multiple potential targets

하지만, TABSA를 풀기 위한 BERT architecture를 사용한 연구들은 많지 않음

3. Approach

Notation

• sentence : \(s\) ( = \(\left\{w_{1}, w_{2}, \ldots w_{n}\right\}\) )

  • target pronouns : \(\left\{w_{i}, \ldots, w_{j}\right\}\)

    from predefined targets \(T= \left\{t_{1}, \ldots, t_{k}\right\}\)

3-1) TABSA task

문장 내의 각각의 target들에 대해 각각의 sentiment 예측하기

• [Input] \(s\), \(T\), \(A=\{\) general, price, transit-location, safety \(\}\)
• [Output] \(y \in\){none, negative, positive \(\}\) for every \(\{(t, a):(t \in T, a \in A)\}\)

3-2) ABSA Task

• [Input] \(s\), \(A=\{\) general, price, transit-location, safety \(\}\)
• [Output] \(y \in\){none, negative, positive \(\}\) for every \(\{a:(a \in A)\}\)

3-3) Context-Guided Softmax Attention

Yang et al(2019)이 제안한 context-aware Transformer model에 기반한 CG-BERT를 사용

( https://seunghan96.github.io/nlp/hbert/Context-Aware-Self-Attention-Networks/ 참고하기 )

\(\left[\begin{array}{c} \hat{\mathbf{Q}}^{h} \\ \hat{\mathbf{K}}^{h} \end{array}\right]=\left(1-\left[\begin{array}{c} \lambda_{Q}^{h} \\ \lambda_{K}^{h} \\ \bar{Q} \end{array}\right]\right)\left[\begin{array}{c} \mathbf{Q}^{h} \\ \mathbf{K}^{h} \end{array}\right]+\left[\begin{array}{c} \lambda_{Q}^{h} \\ \lambda_{K}^{h} \end{array}\right]\left(\mathbf{C}^{h}\left[\begin{array}{c} \mathbf{U}_{Q} \\ \mathbf{U}_{K} \end{array}\right]\right)\).

+ 기존의 알고리즘과는 다르게, \(\lambda_Q^h\)와 \(\lambda_K^h\)가 head 마다 다를 수 있게 함

zero-symemtric gating unit

\(\left[\begin{array}{c} \lambda_{Q}^{h} \\ \lambda_{K}^{h} \end{array}\right]=\tanh \left(\left[\begin{array}{c} \mathbf{Q}^{h} \\ \mathbf{K}^{h} \end{array}\right]\left[\begin{array}{c} \mathbf{V}_{Q}^{h} \\ \mathbf{V}_{K}^{h} \end{array}\right]+\mathbf{C}^{h}\left[\begin{array}{c} \mathbf{U}_{Q} \\ \mathbf{U}_{K} \end{array}\right]\left[\begin{array}{c} \mathbf{V}_{Q}^{C} \\ \mathbf{V}_{K}^{C} \end{array}\right]\right)\).

3-4) Context-Guided Quasi-Attention

QACG-BERT를 제안함 ( Quasi-attention을 (T)ABSA를 위해 사용 )

[ New attention matrix ] :

• linear combination of regular softmax attention matrix & quasi-attention matrix
• \(\hat{\mathbf{A}}^{h}=\mathbf{A}_{\text {Self-Attn }}^{h}+\lambda_{A}^{h} \mathbf{A}_{\text {Quasi-Attn }}^{h}\).

\(\mathbf{A}_{\text {Quasi-Attn }}^{h}\)를 어떻게 구할까?

• quasi-context query \(\mathrm{C}_{Q}^{h}\)
• quasi-context key \(\mathbf{C}_{K}^{h}\) 구하기

\(\left[\begin{array}{c} \mathbf{C}_{Q}^{h} \\ \mathbf{C}_{K}^{h} \end{array}\right]=\mathbf{C}^{h}\left[\begin{array}{l} \mathbf{Z}_{Q} \\ \mathbf{Z}_{K} \end{array}\right]\).

Quasi-attention matrix ( \(\mathbf{A}_{\text {Quasi-Attn }}^{h}\) ) :

\(\mathbf{A}_{Q u a s i-\mathrm{Att} n}^{h}=\alpha \cdot \operatorname{sigmoid}\left(\frac{f_{\psi}\left(\mathbf{C}_{Q}^{h}, \mathbf{C}_{K}^{h}\right)}{\sqrt{d_{h}}}\right)\).

• \(\alpha\) : scaling factor
  • 1로 사용할 것임
• \(f_{\psi}(\cdot)\) : similarity measure ( \(Q\) 와 \(V\) 사이의 )
  • dot product로 사용할 것임
• 따라서, \(\mathbf{A}_{\text {Quasi-Attn }}^{h}\) 는 0~1사이 값

그런 뒤 bidirectional gating factor \(\lambda_A\)를 아래와 같이 설정

\(\begin{gathered} {\left[\begin{array}{c} \lambda_{Q}^{h} \\ \lambda_{K}^{h} \end{array}\right]=\operatorname{sigmoid}\left(\left[\begin{array}{c} \mathbf{Q}^{h} \\ \mathbf{K}^{h} \end{array}\right]\left[\begin{array}{c} \mathbf{V}_{Q}^{h} \\ \mathbf{V}_{K}^{h} \end{array}\right]+\left[\begin{array}{c} \mathbf{C}_{Q}^{h} \\ \mathbf{C}_{K}^{h} \end{array}\right]\left[\begin{array}{c} \mathbf{V}_{Q}^{C} \\ \mathbf{V}_{K}^{C} \end{array}\right]\right)} \\ \lambda_{A}^{h}=1-\left(\beta \cdot \lambda_{Q}^{h}+\gamma \cdot \lambda_{K}^{h}\right) \end{gathered}\).

• \(\beta=1\), \(\gamma=1\)로 설정
• 따라서, \(\lambda_A\)는 0~1사이

최종적인 Attention \(\hat{\mathbf{A}}\)는 -1~2사이에 놓이게 되어있다!

3-5) Classification

마지막 hidden state of CLS 토큰을 사용하여 classification 수행

• 임베딩된 \(e_{\mathrm{CL} \mathrm{S}} \in \mathbb{R}^{1 \times d}\)

최종 output :

• \(y=\operatorname{softmax}\left(e_{\mathrm{CL} S} \mathrm{~W}_{\mathrm{CLS}}^{T}\right)\) .

3-6) Context Matrix

(aspect,target)과 관련 있는 context를 나타내기 위한 single integer 사용

\(\rightarrow\) 이를 embedding 시킴

( total # of possible embeddings : \(\mid t \mid \cdot \mid a \mid\) )

이 context embedding을 hidden vector of each position (=\(\mathbf{E}\) ) 에 concat한 뒤 FFNN에 pass

• \(\mathbf{C}^{h}=\left[\mathbf{E}_{c}, \mathbf{E}\right] \mathbf{W}_{c}^{T}\).
  • \(\mathbf{E}_{c} \in \mathbb{R}^{n \times d}\) : context embedding

3-7) Integration with Pretrained BERT

pretrained BERT model의 weight를 가져와서 initialize!