(PRML) Ch11.Sampling Methods

( Skip the basic parts + not important contents )

11.Sampling Methods

For most probabilsitic models, exact inference is INTRACTABLE!

\(\rightarrow\) Ch11 : approximate inference based on numerical sampling, known as Monte Carlo techniques

Goal : evaluate \(\mathbb{E}[f]=\int f(\mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z}\)

• using finite sum : \(\widehat{f}=\frac{1}{L} \sum_{l=1}^{L} f\left(\mathbf{z}^{(l)}\right)\)
• variance of the estimator : \(\operatorname{var}[\widehat{f}]=\frac{1}{L} \mathbb{E}\left[(f-\mathbb{E}[f])^{2}\right]\)

However, samples \(\mathbf{z}^{(l)}\) may not be independent!

( thus, effective sample size might be much smaller than the apparent sample size )

11-1. Basic Sampling Algorithms

11-1-1. Standard distributions

skip

11-1-2. Rejection Sampling

sample from complex distn

wish to sample from \(p(z)\), which \(p(z)=\frac{1}{Z_{p}} \widetilde{p}(z)\)

• sampling is hard
• evaluation is easy

1) use “proposal distribution” \(q(z)\)

• more simple distribution

2) introduce constant \(k\)

• where \(k q(z) \geqslant \widetilde{p}(z)\)
• \(k q(z)\) : comparison function

Algorithm

• [step 1] generate \(z_0\) from \(q(z)\)

• [step 2] generate \(u_0\) from \(\text{Unif}(0,kq(z_0))\)

• [step 3] if $u_{0}>\widetilde{p}\left(z_{0}\right)$ : reject

  ( o.w : accept )

11-1-3. Adaptive rejection sampling

skip

11-1-4. Importance sampling

Finite sum approximation to expectation

(1) discrete \(z\) space into a uniform grid

(2) evaluate the integrand as a sum : \(\mathbb{E}[f] \simeq \sum_{l=1}^{L} p\left(\mathbf{z}^{(l)}\right) f\left(\mathbf{z}^{(l)}\right)\).

Problem : summation grows exponentially with the dim of \(z\)

Normalized case

finite sum over samples \(\left\{\mathbf{z}^{(l)}\right\}\) drawn from \(q(\mathbf{z})\) :

\(\begin{aligned} \mathbb{E}[f] &=\int f(\mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z} \\ &=\int f(\mathbf{z}) \frac{p(\mathbf{z})}{q(\mathbf{z})} q(\mathbf{z}) \mathrm{d} \mathbf{z} \\ & \simeq \frac{1}{L} \sum_{l=1}^{L} \frac{p\left(\mathbf{z}^{(l)}\right)}{q\left(\mathbf{z}^{(l)}\right)} f\left(\mathbf{z}^{(l)}\right) \end{aligned}\).

we call \(r_{l}=p\left(\mathbf{z}^{(l)}\right) / q\left(\mathbf{z}^{(l)}\right)\), importance weights

Unnormalized case

\(p(\mathrm{z})\) can only be evaluated up to a normalization constant

( \(p(\mathrm{z})=\widetilde{p}(\mathrm{z}) / Z_{p}\) )

\(\begin{aligned} \mathbb{E}[f] &=\int f(\mathbf{z}) p(\mathbf{z}) \mathrm{d} \mathbf{z} \\ &=\frac{Z_{q}}{Z_{p}} \int f(\mathbf{z}) \frac{\widetilde{p}(\mathbf{z})}{\widetilde{q}(\mathbf{z})} q(\mathbf{z}) \mathrm{d} \mathbf{z} \\ & \simeq \frac{Z_{q}}{Z_{p}} \frac{1}{L} \sum_{l=1}^{L} \widetilde{r}_{l} f\left(\mathbf{z}^{(l)}\right) \end{aligned}\).

where \(\tilde{r}_{l}=\tilde{p}\left(\mathbf{z}^{(l)}\right) / \widetilde{q}\left(\mathbf{z}^{(l)}\right) .\)

since \(\begin{aligned} \frac{Z_{p}}{Z_{q}} &=\frac{1}{Z_{q}} \int \tilde{p}(\mathbf{z}) \mathrm{d} \mathbf{z}=\int \frac{\tilde{p}(\mathbf{z})}{\widetilde{q}(\mathbf{z})} q(\mathbf{z}) \mathrm{d} \mathbf{z} \simeq \frac{1}{L} \sum_{l=1}^{L} \widetilde{r}_{l} \end{aligned}\)

\(\mathbb{E}[f] \simeq \sum_{l=1}^{L} w_{l} f\left(\mathbf{z}^{(l)}\right)\), where \(w_{l}=\frac{\tilde{r}_{l}}{\sum_{m} \tilde{r}_{m}}=\frac{\tilde{p}\left(\mathbf{z}^{(l)}\right) / q\left(\mathbf{z}^{(l)}\right)}{\sum_{m} \tilde{p}\left(\mathbf{z}^{(m)}\right) / q\left(\mathbf{z}^{(m)}\right)}\)

11-1-5. Sampling-importance-resampling

skip

11-1-6. Sampling and the EM algorithm

skip

11-2. MCMC

Metropolis algorithm

• when proposal distribution is symmetric
• acceptance probability : \(A\left(\mathrm{z}^{\star}, \mathrm{z}^{(\tau)}\right)=\min \left(1, \frac{\tilde{p}\left(\mathrm{z}^{\star}\right)}{\widetilde{p}\left(\mathrm{z}^{(\tau)}\right)}\right)\).

Metropolis Hastings algorithm

• when proposal distribution does not need to be symmetric

• acceptance probability : \(A_{k}\left(\mathrm{z}^{\star}, \mathrm{z}^{(\tau)}\right)=\min \left(1, \frac{\tilde{p}\left(\mathrm{z}^{\star}\right) q_{k}\left(\mathrm{z}^{(\tau)} \mid \mathrm{z}^{\star}\right)}{\tilde{p}\left(\mathrm{z}^{(\tau)}\right) q_{k}\left(\mathrm{z}^{\star} \mid \mathrm{z}^{(\tau)}\right)}\right)\)

• pf) detailed balance is satisfied!

  \(\begin{aligned} p(\mathbf{z}) q_{k}\left(\mathbf{z} \mid \mathbf{z}^{\prime}\right) A_{k}\left(\mathbf{z}^{\prime}, \mathbf{z}\right) &=\min \left(p(\mathbf{z}) q_{k}\left(\mathbf{z} \mid \mathbf{z}^{\prime}\right), p\left(\mathbf{z}^{\prime}\right) q_{k}\left(\mathbf{z}^{\prime} \mid \mathbf{z}\right)\right) \\ &=\min \left(p\left(\mathbf{z}^{\prime}\right) q_{k}\left(\mathbf{z}^{\prime} \mid \mathbf{z}\right), p(\mathbf{z}) q_{k}\left(\mathbf{z} \mid \mathbf{z}^{\prime}\right)\right) \\ &=p\left(\mathbf{z}^{\prime}\right) q_{k}\left(\mathbf{z}^{\prime} \mid \mathbf{z}\right) A_{k}\left(\mathbf{z}, \mathbf{z}^{\prime}\right) \end{aligned}\).

11-3. Gibbs sampling

1. Initialize \(\left\{z_{i}: i=1, \ldots, M\right\}\)
2. For \(\tau=1, \ldots, T:\) \(-\) Sample \(z_{1}^{(\tau+1)} \sim p\left(z_{1} \mid z_{2}^{(\tau)}, z_{3}^{(\tau)}, \ldots, z_{M}^{(\tau)}\right)\) \(-\) Sample \(z_{2}^{(\tau+1)} \sim p\left(z_{2} \mid z_{1}^{(\tau+1)}, z_{3}^{(\tau)}, \ldots, z_{M}^{(\tau)}\right)\) : \(-\) Sample \(z_{j}^{(\tau+1)} \sim p\left(z_{j} \mid z_{1}^{(\tau+1)}, \ldots, z_{j-1}^{(\tau+1)}, z_{j+1}^{(\tau)}, \ldots, z_{M}^{(\tau)}\right)\) : Sample \(z_{M}^{(\tau+1)} \sim p\left(z_{M} \mid z_{1}^{(\tau+1)}, z_{2}^{(\tau+1)}, \ldots, z_{M-1}^{(\tau+1)}\right)\)

Acceptance ratio = (always) 1

pf) \(A\left(\mathrm{z}^{\star}, \mathrm{z}\right)=\frac{p\left(\mathrm{z}^{\star}\right) q_{k}\left(\mathrm{z} \mid \mathrm{z}^{\star}\right)}{p(\mathrm{z}) q_{k}\left(\mathrm{z}^{\star} \mid \mathrm{z}\right)}=\frac{p\left(z_{k}^{\star} \mid \mathrm{z}_{\backslash k}^{\star}\right) p\left(\mathrm{z}_{\backslash k}^{\star}\right) p\left(z_{k} \mid \mathrm{z}_{\backslash k}^{\star}\right)}{p\left(z_{k} \mid \mathrm{z} \backslash k\right) p(\mathrm{z} \backslash k) p\left(z_{k}^{\star} \mid \mathrm{z} \backslash k\right)}=1\)

11-4. Slice Sampling

difficulties of Metropolis : “sensitive to step size”

• too small : slow decorrelation
• too large : inefficiency due to high rejection rate

Slice sampling : provides an “adaptive step size”

Involves augmenting \(z\) with an additional variable \(u\)

then, draw samples from joint \((z,u)\) space

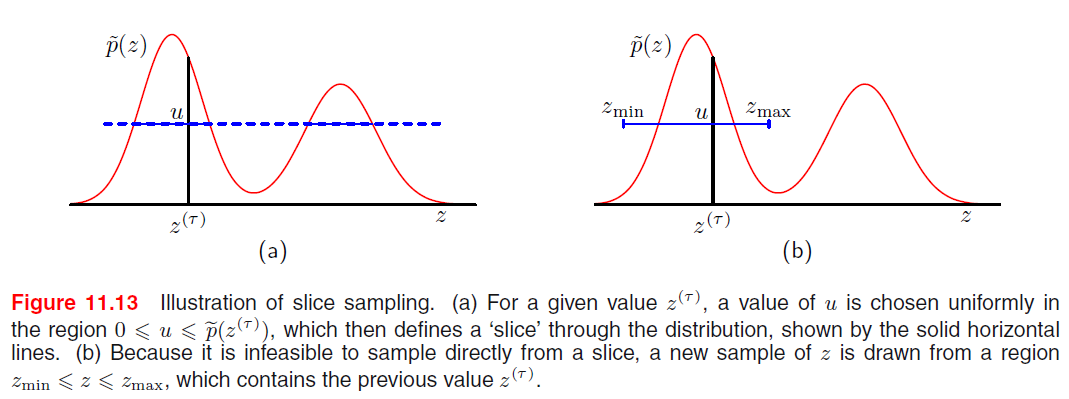
Goal : sample from \(\hat{p}(z, u)=\left\{\begin{array}{ll} 1 / Z_{p} & \text { if } 0 \leqslant u \leqslant \tilde{p}(z) \\ 0 & \text { otherwise } \end{array}\right.\)

where \(Z_{p}=\int \tilde{p}(z) \mathrm{d} z .\)

It is okay to sample from \(\hat{p}(z, u)\) and then just discard \(u\)

\(\int \hat{p}(z, u) \mathrm{d} u=\int_{0}^{\widetilde{p}(z)} \frac{1}{Z_{p}} \mathrm{~d} u=\frac{\tilde{p}(z)}{Z_{p}}=p(z)\).

Algorithm : alternately sample \(z\) and \(u\)

• step 1) given \(z\), evaluate \(\tilde{p(z)}\)
• step 2) sample \(u\) from \(\text{Unif}(0,\tilde{p(z)})\)
• step 3) fix \(u\) and sample \(z\) , distribution defined by \(\{z: \tilde{p}(z)>u\}\)

11-5. The Hybrid MC algorithm

limitation of Metropolis : “random walk”

introduce a sophisticated class of transition, based on physical system

Applicable to..

• distributions over continuous variables
• for which we can readily evaluate the gradient of log probability w.r.t state variable

11-5-1. Dynamic Systems

dynamics : \(\tau\)

state variable : \(z\)

momentum variable : \(r\)

\(r_{i}=\frac{\mathrm{d} z_{i}}{\mathrm{~d} \tau}\).

Hamiltonian function \(H\) : \(H(\mathbf{z}, \mathbf{r})=E(\mathbf{z})+K(\mathbf{r})\)

• \(p(\mathbf{z})=\frac{1}{Z_{p}} \exp (-E(\mathbf{z}))\).
  • \(E(\mathbf{z})\) : potential energy
• \(K(\mathbf{r})=\frac{1}{2}\|\mathbf{r}\|^{2}=\frac{1}{2} \sum_{i} r_{i}^{2}\).
  • kinetic energy

Hamiltonian Equation

• \(\begin{aligned} \frac{\mathrm{d} z_{i}}{\mathrm{~d} \tau} &=\frac{\partial H}{\partial r_{i}} \\ \frac{\mathrm{d} r_{i}}{\mathrm{~d} \tau} &=-\frac{\partial H}{\partial z_{i}} \end{aligned}\).

Properties

• 1) during the evolution of this dynamical system \(H\) is constant

  \(\begin{aligned} \frac{\mathrm{d} H}{\mathrm{~d} \tau} &=\sum_{i}\left\{\frac{\partial H}{\partial z_{i}} \frac{\mathrm{d} z_{i}}{\mathrm{~d} \tau}+\frac{\partial H}{\partial r_{i}} \frac{\mathrm{d} r_{i}}{\mathrm{~d} \tau}\right\} \\ &=\sum_{i}\left\{\frac{\partial H}{\partial z_{i}} \frac{\partial H}{\partial r_{i}}-\frac{\partial H}{\partial r_{i}} \frac{\partial H}{\partial z_{i}}\right\}=0 \end{aligned}\).

• 2) Liouville’s Theorem : preserve volume in phase space

  \[\mathbf{V}=\left(\frac{\mathrm{d} \mathbf{z}}{\mathrm{d} \tau}, \frac{\mathrm{d} \mathbf{r}}{\mathrm{d} \tau}\right)\]

  \(\begin{aligned} \operatorname{div} \mathbf{V} &=\sum_{i}\left\{\frac{\partial}{\partial z_{i}} \frac{\mathrm{d} z_{i}}{\mathrm{~d} \tau}+\frac{\partial}{\partial r_{i}} \frac{\mathrm{d} r_{i}}{\mathrm{~d} \tau}\right\} \\ &=\sum_{i}\left\{-\frac{\partial}{\partial z_{i}} \frac{\partial H}{\partial r_{i}}+\frac{\partial}{\partial r_{i}} \frac{\partial H}{\partial z_{i}}\right\}=0 \end{aligned}\).

Joint pdf

• total energy = Hamiiltonian
• \(p(\mathbf{z}, \mathbf{r})=\frac{1}{Z_{H}} \exp (-H(\mathbf{z}, \mathbf{r}))\).

Due to 2 properties : Hamiltonian dynamics will leave \(p(z,r)\) invariant

• volume of this region will remain unchanged
• thus, \(H\), and probability density will remain unchanged

Althoough \(H\) is invariant, \(z\) and \(r\) will vary

In order to arrive at an ergodic sampling…

\(\rightarrow\) introduce additional moves

\(\rightarrow\) change the value of \(H\) while leaving \(p(z,r)\) unchanged!

By “replacing \(z\) with one drawn from its distribution conditioned on \(z\) “

( \(z\) and \(r\) are independent in \(p(z,r)\), so conditional \(p(r\mid z)\) is a Gaussian )

Leapfrog discretization

successive updates to position (\(z\)) and momentum \((r)\)

\[\begin{aligned} \widehat{r}_{i}(\tau+\epsilon / 2) &=\widehat{r}_{i}(\tau)-\frac{\epsilon}{2} \frac{\partial E}{\partial z_{i}}(\widehat{\mathbf{z}}(\tau)) \\ \widehat{z}_{i}(\tau+\epsilon) &=\widehat{z}_{i}(\tau)+\epsilon \widehat{r}_{i}(\tau+\epsilon / 2) \\ \widehat{r}_{i}(\tau+\epsilon) &=\widehat{r}_{i}(\tau+\epsilon / 2)-\frac{\epsilon}{2} \frac{\partial E}{\partial z_{i}}(\widehat{\mathbf{z}}(\tau+\epsilon)) \end{aligned}.\]

• time interval : \(\tau\) \(\rightarrow\) need \(\tau/\epsilon\) steps

Summary

Hamiltonian dynamical approach invloves alternating between

• series of leapfrog updates
• re-sampling of the momentum variables

Unlike Metropolis, able to make use of “gradient of log prob”

11-5-2. Hybrid MC

Hybrid MC = Hamiltonian dynamics + Metropolis

After each application of leapfrog…

• resulting candidate state is ACCEPTED/REJECTED according to the Metropolis criterion

  ( based on the value of Hamiltonian \(H\) )

  \(\min \left(1, \exp \left\{H(\mathbf{z}, \mathbf{r})-H\left(\mathbf{z}^{\star}, \mathbf{r}^{\star}\right)\right\}\right)\).

• perfect : \(H\) unchanged \(\rightarrow\) 100% accept

• numerical errors : \(H\) may sometimes decrease