( 참고 : Fastcampus 강의 )

[ 17. Time Difference Learning 실습 ]

1. 환경 설정하기

1-1. Import Packages

import sys; sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt

from src.part2.temporal_difference import TDAgent
from src.common.gridworld import GridworldEnv
from src.common.grid_visualization import visualize_value_function, visualize_policy

np.random.seed(0)

1-2. Make Environment

nx, ny = 4, 4
env = GridworldEnv([ny, nx])

1-3. Environment 소개

print(env.nS) ## 16
print(env.nA) ## 4
print(env.P_tensor.shape) # 4x16x16
print(env.R_tensor.shape) # 16x4

2. Agent 초기화

td_agent = TDAgent(gamma=1.0,
                   num_states=nx * ny,
                   num_actions=4,
                   epsilon=1.0,
                   lr=1e-2,
                   n_step=1)

Agent의 input

gamma : 감가율
num_states : 상태공간의 크기 (4x4)
num_actions : 행동공간의 크기 (4)
epsilon: \(\epsilon\)-greedy policy의 parameter
lr : learning rate (=\(\alpha\))
n_step : 스텝 수

3. 1-step TD ( = TD(0) )

\(V(s) \leftarrow V(s) + \alpha (G_t - V(s))\) .

where \(G_t = R_{t+1} + \gamma V(s_{t+1})\).

(1) 1-step TD로 update하는 함수

def sample_update(self, state, action, reward, next_state, done):
    # (1) G_t ( = td_target ) 계산하기
    td_target = reward + self.gamma * self.v[next_state] * (1 - done)
    # (2) V_s 업데이트하기
    self.v[state] += self.lr * (td_target - self.v[state])

(2) 1번의 epsiode를 run

def run_episode(env, agent):
    ## 환경 초기화
    env.reset()
    while True:
        # (1) state 관측
        state = env.observe()
		# (2) action 취함
        action = agent.get_action(state)
        # (3) reward & next state 돌려받음
        next_state, reward, done, info = env.step(action)
        # (4) UPDATE하기 ( TD(0) )
        agent.sample_update(state=state, 
                            action=action, 
                            reward=reward,
                            next_state=next_state,
                            done=done)
        
        if done:
            break

(3) 여러 번의 epsiode를 run

총 10,000번의 episode를 run 한다 ( log를 매 1,000번마다 출력 )

num_episode = 10000
print_log = 1000

def run_episodes(env, agent, num_episode, print_log):
    values = []
    log_iters = []
    
    for i in range(num_episode+1):  
        run_episode(env, agent)

        if i % print_log == 0:
            values.append(agent.v.copy())
            log_iters.append(i)
    
    info = dict()
    info['values'] = values
    info['iters'] = log_iters
    return info

10,000번의 episode 수행

td_agent.reset_values()
info = run_episodes(env, td_agent, num_episode, print_log)

(4) Variance of TD(0) Predictions

Stochastic 하기 때문에, 매번 실행할 때마다 계산된 value function이 다르다.

그렇다면, 여러번 계산 된 value function의 variance는?

3,000번의 epsiode를 run하는 과정을 총 10번 반복

reps = 10
num_episode = 3000
print_log = 30

10번 반복한 결과를 values_over_runs에 저장

size : 10x101x16
- 10 : 총 10번 반복
- 101 : 3000번의 epsiode를 30간격으로 저장 (0,30,60,90,…,3000) …총 101회
- 16 : state의 개수 (4x4)

values_over_runs = []

for i in range(reps):
    td_agent.reset_values()
    print("start to run {} th experiment ... ".format(i))
    info = run_episodes(env, td_agent, num_episode, print_log)
    values_over_runs.append(info['values'])
    
values_over_runs = np.stack(values_over_runs)
print(values_over_runs.shape) # 10,101,16

Calculate answer ( using DP )

from src.part2.tensorized_dp import TensorDP

dp_agent = TensorDP()
dp_agent.set_env(env)

v_pi = dp_agent.policy_evaluation()
v_pi_expanded = np.expand_dims(v_pi, axis=(0,1))

Calculate Error ( & mean.std of error )

errors = np.linalg.norm(values_over_runs - v_pi_expanded, axis=-1)
error_mean = np.mean(errors, axis=0)
error_std = np.std(errors, axis=0)

Visualization

fig, ax = plt.subplots(1,1, figsize=(10,5))
ax.grid()
ax.fill_between(x=info['iters'],
                y1=error_mean + error_std,
                y2=error_mean - error_std,
                alpha=0.3)
ax.plot(info['iters'], error_mean, label='Evaluation error')
ax.legend()
_ = ax.set_xlabel('episodes')
_ = ax.set_ylabel('Errors')

4. n-step TD

\(V(s) \leftarrow V(s) + \alpha (G_t^{n} - V(s))\) .

where \(G_t^{n} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n})\).

(1) Agent 설정

step 수는 5로

n_steps = 5
n_step_td_agent = TDAgent(gamma=1.0,
                          num_states=nx * ny,
                          num_actions=4,
                          epsilon=1.0,
                          lr=1e-2,
                          n_step=n_steps)

(2) n-step TD로 update하는 함수

유의점 : example ) episode length=10, t=9,n=2

\(\rightarrow\) \(S_{11}\)은 존재하지 않는다! HOW..??

\(\rightarrow\) terminal state에 도착하면, “0”이다!

def update(self, episode):
    states, actions, rewards = episode
    
	# 해당 epsiode의 길이 ( state의 개수)
    episode_length = len(states)
    
	# (n_step+1)회 만큼의 state를 섞는다
    states += [0] * (self.n_step + 1)  # dummy states
    rewards += [0] * (self.n_step + 1)  # dummy rewards
    dones = [0] * episode_length + [1] * (self.n_step + 1)

	# 할인율(discount) 계수를 곱해주는 kernel
    kernel = np.array([self.gamma ** i for i in range(self.n_step)])
    
    for i in range(episode_length):
        s = states[i]
        ns = states[i + self.n_step]
        done = dones[i]

        # n-step TD target 계산하기
        ## (1) R 부분
        g = np.sum(rewards[i:i + self.n_step] * kernel)
        ## (2) V 부분
        g += (self.gamma ** self.n_step) * self.v[ns] * (1 - done)
        
        # value function 업데이트하기
        self.v[s] += self.lr * (g - self.v[s])

이하 과정은 TD(0)와 동일하므로 생략

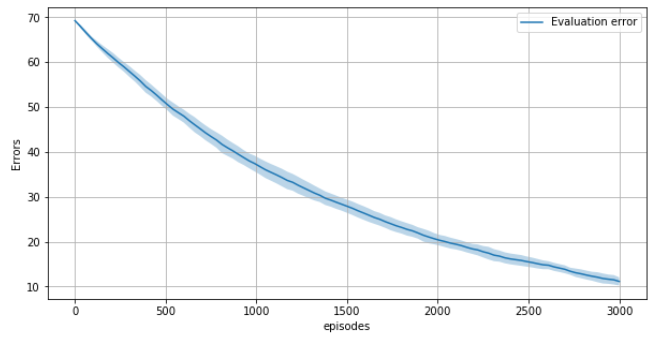
5. TD(0) vs n-step TD vs MC

Twitter Facebook LinkedIn

17.Time Difference Learning 실습

Seunghan Lee