40.(paper 5) A3C (Asynchronous Advantage Actor Critic)

( 참고 : Fastcampus 강의 )

[ 40.(paper 5) A3C (Asynchronous Advantage Actor Critic) ]

1. Asynchronous란?

Asynchronous = “비동기적”

• (1) 기존의 “동기적” 학습

• (2) 제안하는 “비동기적” 학습

(1) 기존의 “동기적” 학습

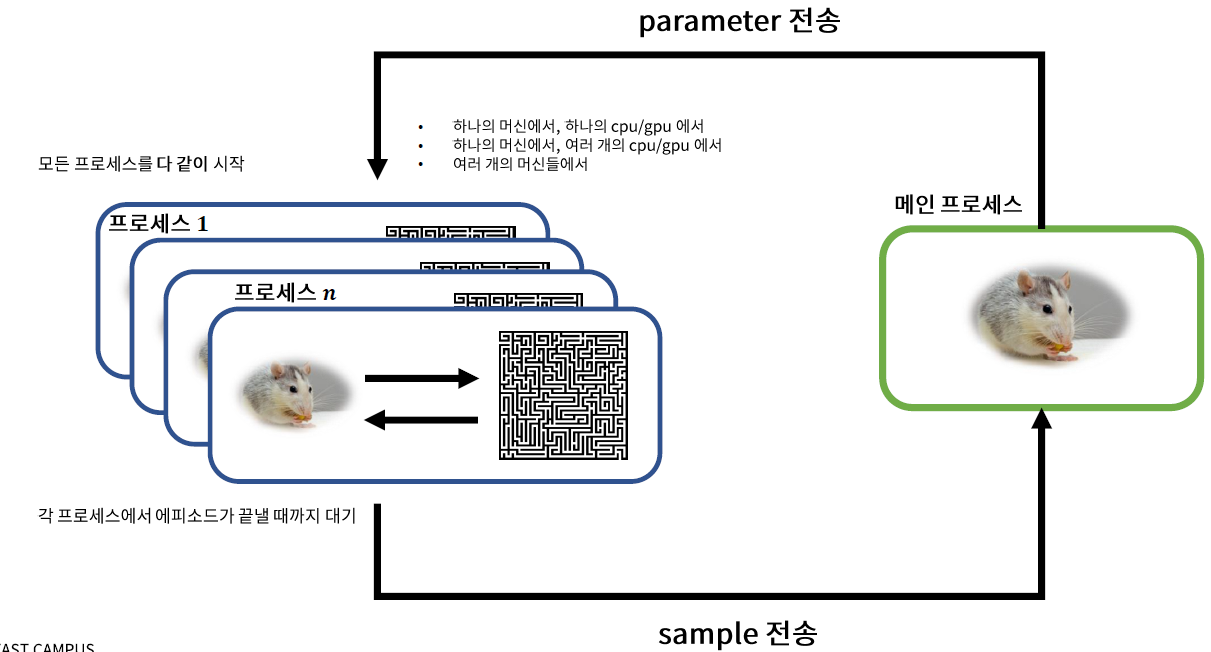
• \(n\)개의 process를 수행
  • 각 process = agent & environment가 상호 작용하는 하나의 simulation
  • 각 process 내에 main process의 \(\theta\)가 복제되어 있음
• \(n\)개의 process가 모두 끝난 뒤에 한번에 main process를 update

(2) 제안하는 “비동기적” 학습

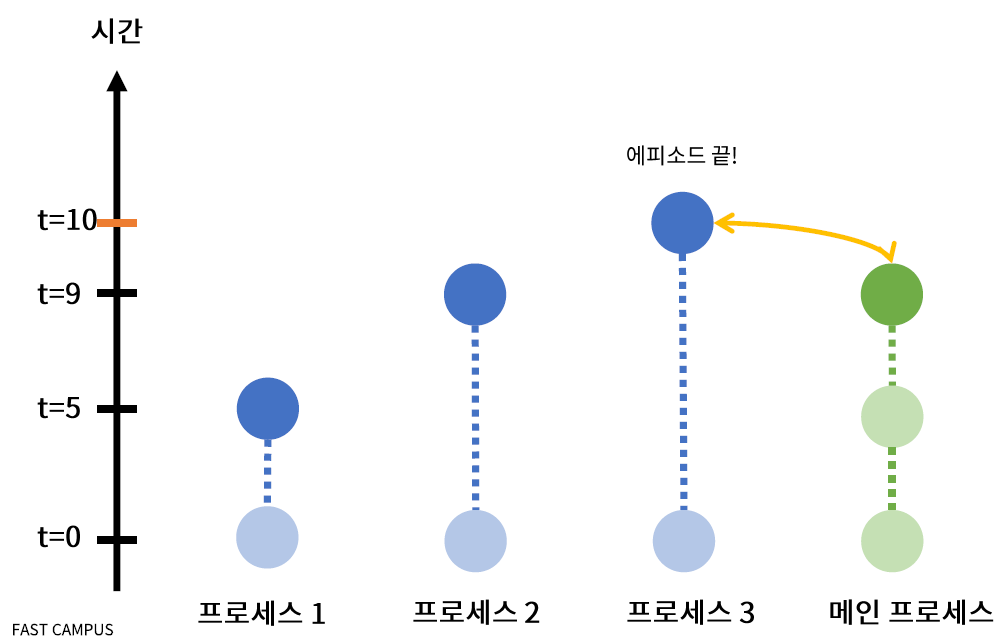
• 마찬가지로 \(n\)개의 process를 수행

  ( process 별로 episode length가 다를 수 있다 )

• **“먼저 끝난 애는 먼저 main process에 반영” **

  ( + main process로 parameter로 바로 동기화 )

2. Asynchronous Methods for Deep RL

이 논문에서는 크게 3가지의 동기적 RL를 비동기적 RL로 바꿔서 품

• 1) Deep Q-learning 계열

• 2) Deep SARSA 계열

• **3) A2C계열 ( = TD Actor-critic ) **

  • https://seunghan96.github.io/rl/30.Actor-Critic/ 참고

모든 방법에서 발견된 공통점

• 각 process 별로 다른 양상의 epsiode

  ( = exploration GOOD )

• 알고리즘 학습이 안정적

(1) Deep Q-learning 계열

1개의 Process에서 이루어지는 과정 :

설명

[1] \(Q\)-learning의 target을 계산

[2] Gradient Accumulation

• 기존) mean

• 제안) **summation ( 매 step마다 cumulative하게 더한다 ) **

  WHY? 구현의 귀찮음 피하고자..?

  • \(\frac{d \mathcal{L}_{n}}{d \theta}=\frac{1}{T_{n}} \sum_{t=1}^{T_{n}} \frac{\partial\left(Q\left(s_{t}, a_{t}\right)-r_{t}+\gamma \max _{a^{\prime}} Q_{\theta}\left(s_{t+1}, a^{\prime}{ }_{t+1}\right)\right)^{2}}{\partial \theta}\).
  • \(\frac{d \mathcal{L}}{d \theta}=\frac{1}{\sum_{n=1}^{N} T_{n}} \sum_{n=1}^{N} T_{n} \frac{d \mathcal{L}_{n}}{d \theta} \neq \frac{1}{N} \sum_{n=1}^{N} \frac{d \mathcal{L}_{n}}{d \theta}\). ( \(T_n\)이 서로 다를 수 있으므로 )ㄹ

[3] Global Target Network 업데이트

[4] Global Main Network 업데이트

(2) A2C 계열

• 기존의 TD-Actor Critic : on-policy / exploration 부족
• “Entropy Regularization” 통한 exploration 장려

Actor Gradient : \(\nabla_{\theta} J(\theta)=\sum_{t=1}^{T} \mathbb{E}_{\pi}\left[\nabla_{\theta} \ln \pi_{\theta}\left(a_{t} \mid s_{t}\right) \delta_{\psi}\left(s_{t}, a_{t}\right)\right]+\beta \nabla_{\theta} \mathcal{H}\left(\pi_{\theta}\left(a_{t} \mid s_{t}\right)\right)\)

• 마지막 regularization term을 보면, Entropy가 높아지길 장려함을 알 수 있음

  ( = random한 ( 고른 ) action 을 유도함 )

Actor Gradient Term 해석

• term 1) (regularization 앞 부분) exploitation
• term 2) (regularization 부분) exploration

A3C의 전체 Pseudocode