42.(paper 7) Soft Actor Critic (SAC)

( 참고 : Fastcampus 강의 )

[ 42.(paper 7) Soft Actor Critic (SAC) ]

[paper] Soft Actor-Critic: Off-Policy Maximum Entropy Deep …

1. Background

SAC = (1) + (2) + (3)

• (1) DDPG의 “Off-Policy”
  • DDPG = (1) DQN + (2) Determinstic Policy Gradient
  • 연속적인 행동공간 OK
  • Deterministic Policy 사용으로 인해 Off-policy 사용 가능
  • Loss Function
    • Critic 학습 시 : Bellman Error
    • Actor 학습 시 : Determinstic Policy Gradient
• (2) Soft Q-learning의 “Soft-Bellman 방정식”
• (3) TD3의 “Actor-Critic 안정화”
  • Actor Critic의 Maximization Bias를 해결하기 위해 제안
  • 2개의 독립된 Q-Function을 계산하는 NN ( + 각각에 해당하는 target network도 ) + 1개의 Actor Network
  • Action에 exploration (Gaussian) noise
  • Target Smoothing noise

2. Maximum Entropy RL

(Policy Gradient에서의) loss function

• 일반 RL :

  \(J(\pi)=\sum_{t=0}^{T} E_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi}}\left[r\left(s_{t}, a_{t}\right)\right]\).

• Maximum Entropy RL :

  \(J(\pi)=\sum_{t=0}^{T^{*}} E_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi}}\left[r\left(s_{t}, a_{t}\right)+\alpha \mathcal{H}\left(\pi\left(a_{t} \mid s_{t}\right)\right)\right]\).

  • where \(\alpha\) = “temperature parameter”

  • 해석 : Policy Gradient의 일반적인 loss + ENTROPY BONUS

    ( “entropy 값이 높도록” = “다양한 행동을 하도록” = “exploration” 유도 )

  • 매 순간순간 최대한 Random하게 움직여라!

Advantages

• 1) better EXPLORATION
• 2) 외부의 noise에 ROBUST
• 3) 다양한 \(\pi^{*}(a_t \mid s_t)\) 학습 가능

보상함수가 새로워짐

• (before) \(r\left(s_{t}, a_{t}\right)\)
• (after) \(r\left(s_{t}, a_{t}\right)+\alpha \mathcal{H}\left(\pi\left(a_{t} \mid s_{t}\right)\right)\).

\(\rightarrow\) NEW Poliy Iteration 알고리즘 필요

( Policy Iteration 복습)

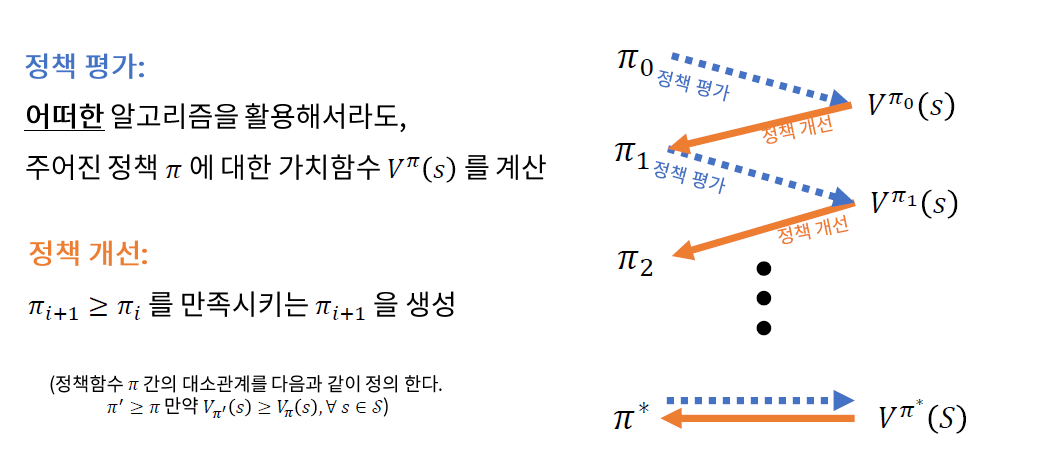
즉, 새로운

• (1) Policy Evaluation
• (2) Policy Improvement

를 파악할 필요가 있다

3. (Soft) Policy Iteration

(1) (Soft) Policy Evaluation

• Value Function 부분에 “Entropy Term”이 더해진 것을 확인할 수 있다.

(2) (Soft) Policy Improvement

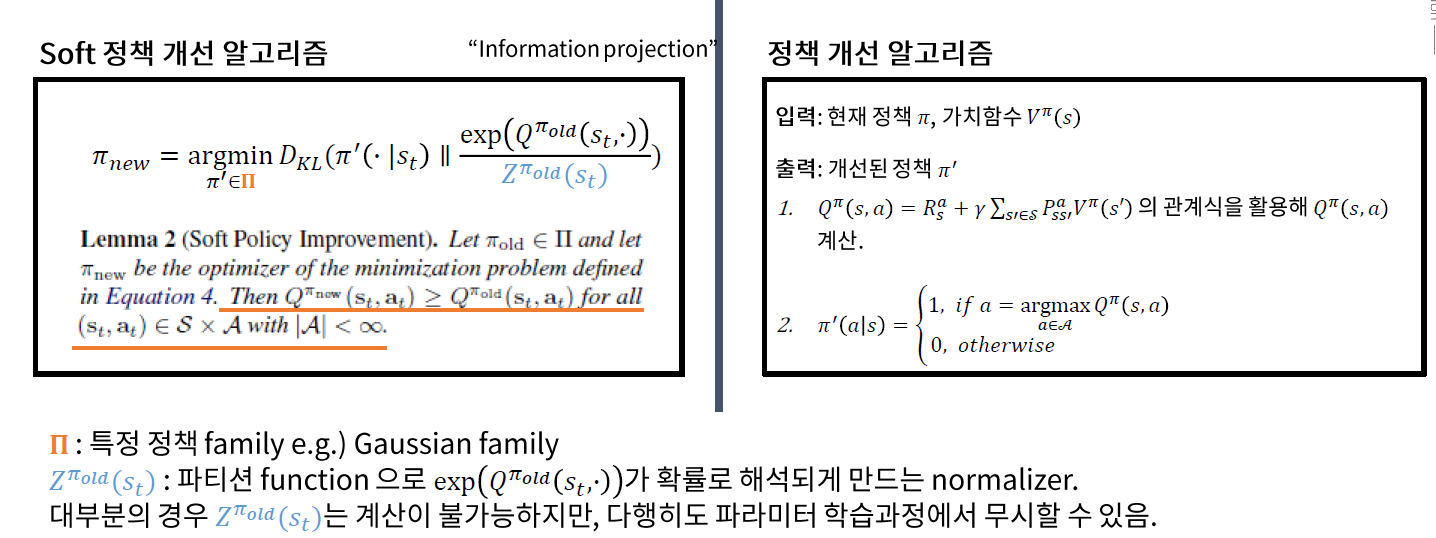
• 쉽게 풀기 위해, policy function에 Exponential Family ( 그 중 Gaussian ) 가정을 한다
• normalizing constant는 무시 가능 ( during implementation )

비교

(1) 기존의 P.I

• \(Q\)를 최대화 시키는 \(a\)를 최적의 policy로 삼음 ( = 해당 행동에는 1, 나머지는 전부 0 )

(2) Soft P.I

• \(\pi_{n e w}=\underset{\pi^{\prime} \in \Pi}{\operatorname{argmin}} D_{K L}\left(\pi^{\prime}\left(\cdot \mid s_{t}\right) \mid \mid \frac{\exp \left(Q^{\pi_{\text {old }}}\left(s_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}\left(s_{t}\right)}}\right)\).

• 위 식의 직관적 해석 :

  • “추산한 Q값이 높다면, 해당 action의 확률을 높이고, 아니면 낮추자!”

    ( = Q값에 비례/비슷하게끔 설계 )

• “Information Projection”

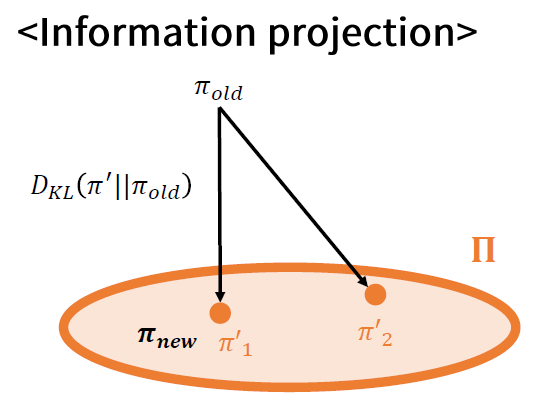
(Proof) 아래 PPT 자료 참고

Information Projection을 통해 정책을 improve하면, 더 나아질 수 밖에 없음을 증명!

4. Training SAC

(1) Training “Critic”

Network 2개 : Q Network (\(\theta\)) & Target Network (\(\bar{\theta}\)) )

LOSS FUNCTION : \(J_{Q}(\theta)=\mathbb{E}_{\left(s, a, s^{\prime}\right) \sim D}\left[\frac{1}{2}\left(Q_{\theta}(s, a)-\left(r(s, a)+\gamma\left(Q\left(s^{\prime}, a^{\prime}\right)+\alpha \mathcal{H}\left(\pi\left(\cdot \mid s^{\prime}\right)\right)\right)\right)\right)^{2}\right]\).

[ 제안된 방법 ]

• (full MC) 대신에

  \(J_{Q}(\theta)=\mathbb{E}_{\left(s, a, s^{\prime}\right) \sim D}\left[\frac{1}{2}\left(Q_{\theta}(s, a)-\left(r(s, a)+\gamma \mathbb{E}_{s^{\prime} \sim p}\left(V_{\bar{\theta}}\left(s^{\prime}\right)\right)\right)\right)^{2}\right]\).

• (one sample MC) 로 근사함

  \(J_{Q}(\theta)=\mathbb{E}_{\left(s, a, s^{\prime}\right) \sim D}\left[\frac{1}{2}\left(Q_{\theta}(s, a)-\left(r(s, a)+\gamma\left(Q\left(s^{\prime}, a^{\prime}\right)+\alpha \mathcal{H}\left(\pi\left(\cdot \mid s^{\prime}\right)\right)\right)\right)\right)^{2}\right]\).

Target이 다음과 같이 바뀜을 알 수 있다.

• (before) \(r(s, a)+\gamma \mathbb{E}_{s^{\prime} \sim p}\left(V_{\bar{\theta}}\left(s^{\prime}\right)\right)\).

• (after) \(r(s, a)+\gamma\left(Q\left(s^{\prime}, a^{\prime}\right)+\alpha \mathcal{H}\left(\pi\left(\cdot \mid s^{\prime}\right)\right)\right)\).

  \(\mathbb{E}_{s^{\prime} \sim p}\left(V_{\bar{\theta}}\left(s^{\prime}\right)\right)\) 의 expectation을 1 sample MC로 근사함

  ( \(Q\left(s^{\prime}, a^{\prime}\right)+\alpha \mathcal{H}\left(\pi\left(\cdot \mid s^{\prime}\right)\right)\) 로 대신함 )

(2) Training “Actor”

Network 1개 : Actor Network

LOSS FUNCTION : \(E_{\left(s_{t}, a_{t}\right) \sim D}\left[D_{K L}\left(\pi_{\phi}\left(\cdot \mid s_{t}\right) \mid \mid \frac{\exp \left(Q_{\theta}\left(s_{t}, \cdot\right)\right)}{Z_{\theta}\left(s_{t}\right)}\right)\right]\).

[ 제안된 방법 ] Reparameterization Trick (VAE에서 제안된 trick)

• lower variance
• back-prop은 deterministic한 부분만 타고 흐른다.

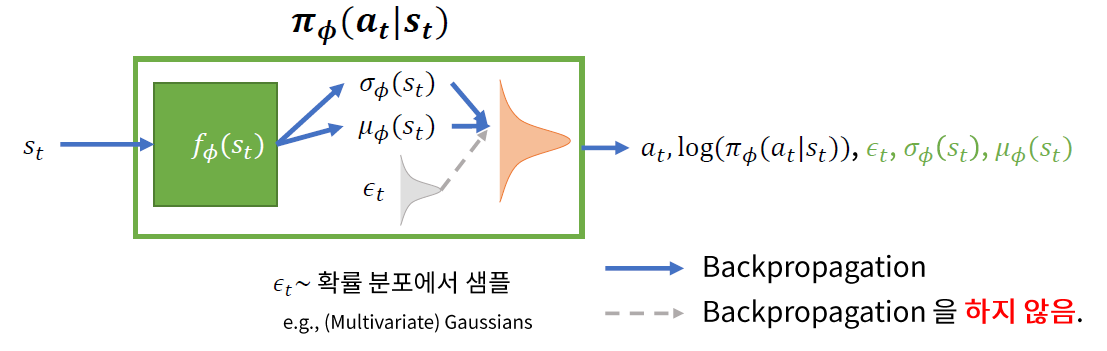
(a) Loss Function ( w.o. Reparam trick )

• \(J_{\pi}(\phi)E_{\left(s_{t}, a_{t}\right) \sim D}\left[D_{K L}\left(\pi_{\phi}\left(\cdot \mid s_{t}\right) \mid \mid \frac{\exp \left(Q_{\theta}\left(s_{t}, \cdot\right)\right)}{Z_{\theta}\left(s_{t}\right)}\right)\right]\).

(b) Loss Function ( with Reparam trick )

• \(J_{\pi}(\phi)=E_{s_{t} \sim D, \epsilon_{t} \sim \mathcal{N}}\left[\log \pi_{\phi}\left(f_{\phi}\left(\epsilon_{t} ; s_{t}\right) \mid s_{t}\right)-Q_{\theta}\left(s_{t}, f_{\phi}\left(\epsilon_{t} ; s_{t}\right)\right)\right]\).

(c) Gradient of Loss Function ( with Reparam trick )

• \(\tilde{\nabla}_{\phi} J_{\pi}(\phi)=\nabla_{\phi} \log \pi_{\phi}\left(a_{t} \mid s_{t}\right)+\left(\nabla_{a_{t}} \log \pi_{\phi}\left(a_{t} \mid s_{t}\right)-\nabla_{a_{t}} Q\left(s_{t}, a_{t}\right)\right) \nabla_{\phi} f_{\phi}\left(\epsilon_{t} ; s_{t}\right)\).

  where \(a_t = f_{\phi}\left(\epsilon_{t} ; s_{t}\right)\)

5. Others

Temperature Parameter

\(J(\pi)=\sum_{t=0}^{T^{*}} E_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi}}\left[r\left(s_{t}, a_{t}\right)+\alpha \mathcal{H}\left(\pi\left(a_{t} \mid s_{t}\right)\right)\right]\) 에서, \(\alpha\)는 temperature parameter이다.

• ( 첫 번째 SAC ) \(\alpha=1\)
• ( 후속 SAC ) \(\alpha\) = hyper-parameter
• ( SAC 확장판 ) \(\alpha\) = parameter

6. Pseudocode