( 출처 : 연세대학교 데이터베이스 시스템 수업 (CSI6541) 강의자료 )
Chapter 2. Intro to Relational Model
2-1. Structure of Relational DB
(1) Relation
Notation
- sets : \(D_1\) \(\cdots\) \(D_n\)
- relation \(r\) : subset of \(D_1 \times D_2 \times \cdots D_n\)
order of tuples is irrelavent
(2) Relation Schema
each attribute of a relation has a name
Notation
- \(A_1, \cdots A_n\) : \(n\) attributes
- \(R=(A_1, \cdots A_n)\) : relation schema
- \(r(R)\) : relation on the \(R\)
Domain (of the attribute)
- set of allowed values for each attribute
Example
- \(R\) : Instructor-schema = (ID, name, dept_name, salary)
- \(r(R)\) : Instructor(Instructor-schema)
(3) Keys
Examples )
- relation schema : \(R = (A_1 \cdots A_n)\)
- ex) \(R\) = (sid, sname, ssn, dname, gpa)
- key : \(K \subset R\)
Types of keys
- (1) super key
- if \(K\) is sufficient to identify a unique tuple of each possible relation
- Ex) \(K_1\) = (sid, sname), \(K_2\) = (sname, dname)
- (2) candidate key
- If \(K\) is super key & it is minimal
- Ex) \(K_3\) = (sid)
- (3) primary key
- if \(K\) is a candidate key & chosen by a DB designer as a means of identifying tuples
- Ex) \(K_4\) = (ssn)

(4) Query Languages
Language with which user requests information from the database
Categories of languages
- (1) procedural
- (2) non-precedural
Pure languages
- (procedural) relational algebra
- (non-procedural) tuple relational calculus
- (non-procedural) domain relational calculus
\(\rightarrow\) form underlying basis of query langauges
2-2. Relational Algebra
- procedural language
- 6 basic operators
- select / project / union / set-difference / cartesian product / rename
- IN & OUT of operators
- [IN] one or more relations
- [OUT] new relation
(1) Select
Input : relation \(r\)
Output : \(\sigma_{A=B} \wedge D>5(r)\)
- cond 1 : A = B
- cond 2 : D > 5
(2) Project
Input : relation \(r\)
Output : \(\prod_{A,C}(r)\)
-
just choose 2 attributes(columns), A & C
( + drop duplicate data )
(3) Union
Input : relation \(r\) & \(s\)
Output : \(r \cup s\)
- Add rows ( but, drop duplicates )
(4) Set Difference
Input : relation \(r\) & \(s\)
Output : \(r-s\)
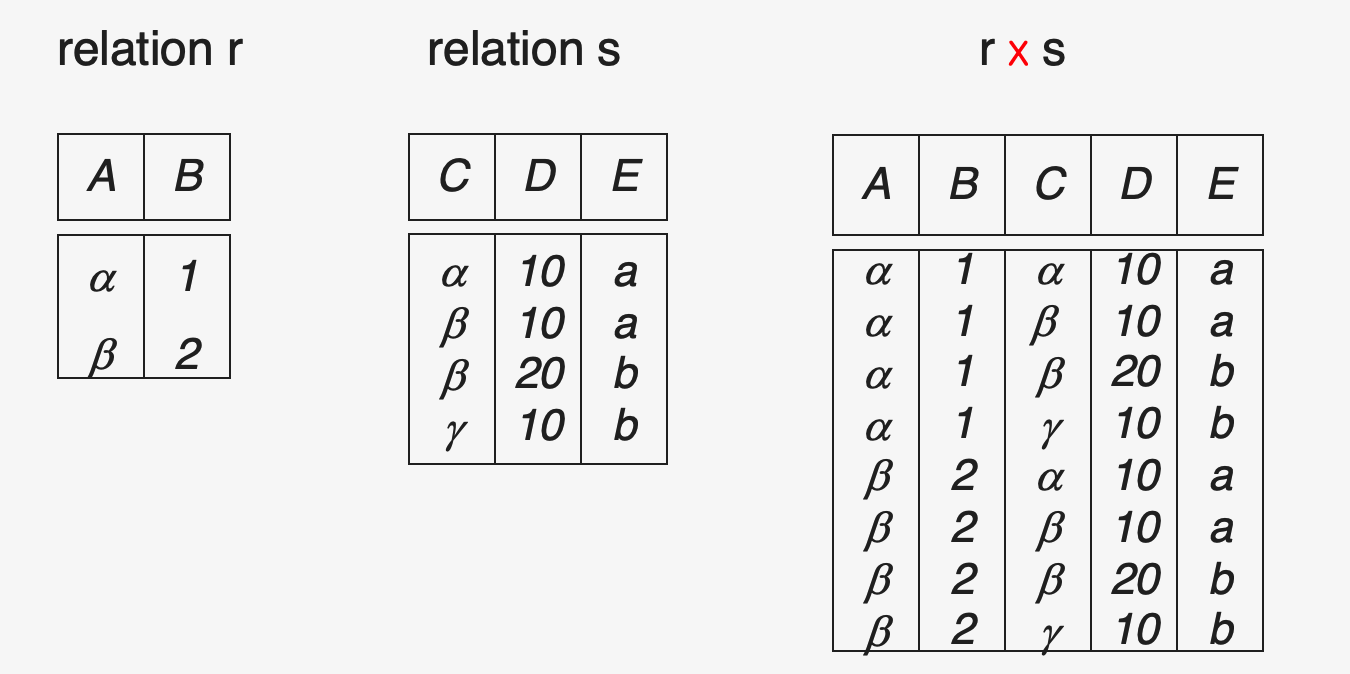
(5) Cartesian Product
Input : relation \(r\) & \(s\)
Output : \(r\times s\)
(6) Rename
-
name the results of relational-algebra expressions
- allow us to refer to a relation by more than one name
- \(\rho_x(E)\) : expression \(E\) under name \(x\)
- \(\rho_{x(A_1, \cdots A_n)}(E)\) . : expression \(E\) under the name \(x\) & with attributes renamed to \(A_1 \cdots A_n\)
(7) Additional Operations
do not add any power to the relational algebra
( just simplify common queries )
- set intersection : \(\mathrm{r} \cap \mathrm{s}=\mathrm{r}-(\mathrm{r}-\mathrm{s})\)
- natural join : \(r \bowtie S\)
- division : \(r \div S\)
- assignment : temp1 \(\leftarrow \prod_{\mathrm{R}-\mathrm{s}}(r)\)
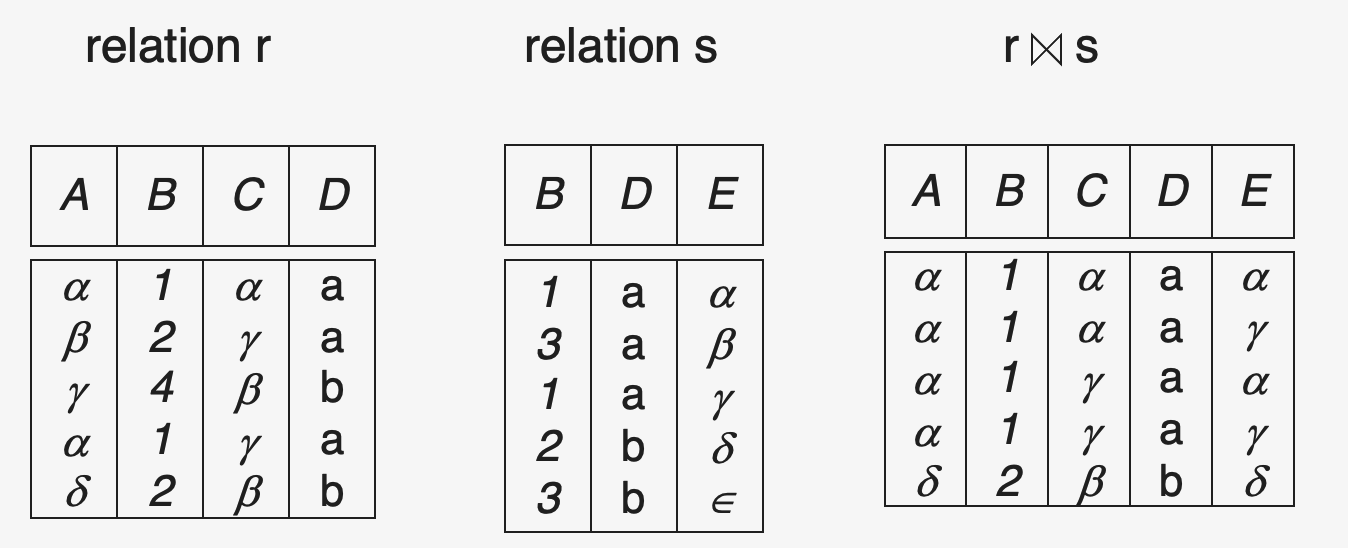
natural join
settings
- \(r\) : relation on schema \(R\)
- \(s\) : relation on schema \(S\)
input : \(r\) & \(s\)
output : \(r \bowtie S\)
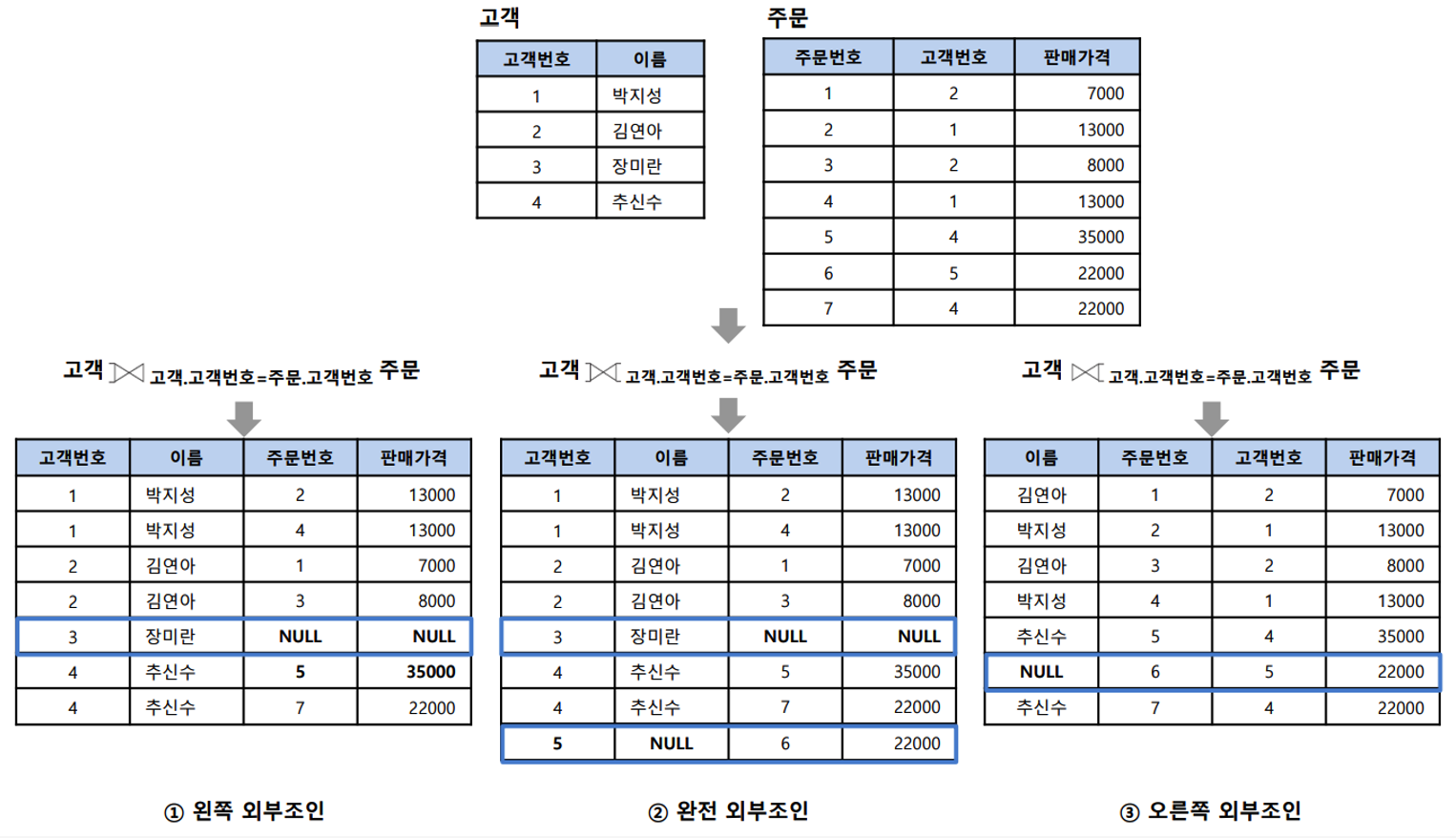
outer join
-
extension of the join operation that avoids loss of information
- use null values
- ex) LEFT outer join, RIGHT outer join, FULL outer join