( 출처 : 연세대학교 데이터베이스 시스템 수업 (CSI6541) 강의자료 )
Chapter 9. Indexing and Hashing
Contents
- Basic Concepts
- Ordered Indices
- ..
(1) Basic Concepts
Indexing mechanisms
- used to speed up access to desired data
Search Key :
- set of attributes used to look up records in a file
Index file …
- consists of records (called index entries) of the form search-key & pointer
- typically much smaller than the original file
2 basic kinds of indices
- (1) ordered indices
- search keys are stored in sorted order
- (2) hash indices
- search keys are distributed uniformly across “buckets” using a “hash function”
(2) Ordered Indicies
( stored in sorted order of search key value )
If the file containing the records is sequentially ordered…
-
(1) primary index
( = also called clustering index )
- index whose search key also defines the sequential order of the file
-
(2) secondary index
( = also called non-clustering index )
- index whose search key specifies an order different from the sequential order of the file
Indexed sequential file :
- sequential file with a primary index
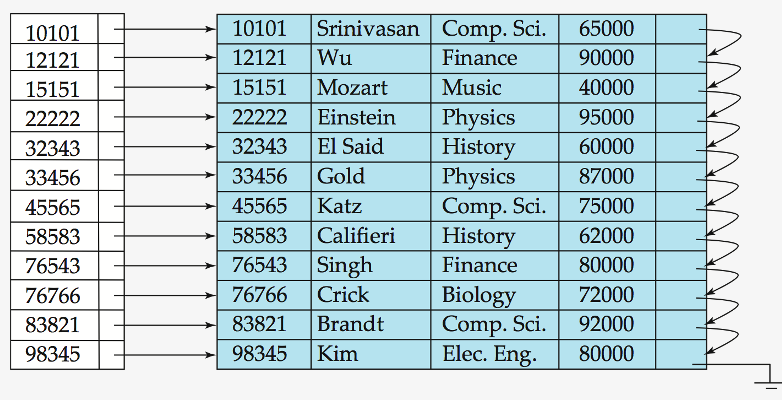
Primary Index : Dense Index Files
-
data의 “모든 key가 index에서 표현”
-
Dense Index : “key들을 data의 순서와 동일하게 유지”
-
Index : key & pointer만을 보유
\(\rightarrow\) data 자체보다 훨씬 적은 공간 소모
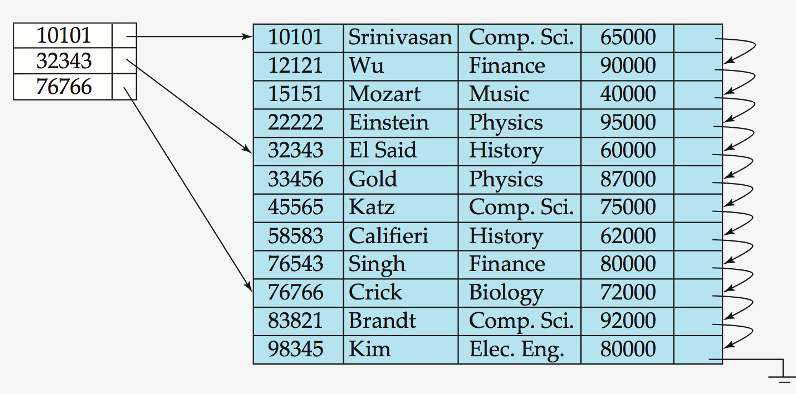
Primary Index : Sparse Index Files
-
(Dense Index) 모든 key를 가지고 있기엔, data가 너무 많음
\(\rightarrow\) 이를 보완하기 위한 것이 Sparse Index
-
data (X) data block (O) 마다 1개의 key-pointer 쌍을 가짐
-
장 & 단 ( vs. Dense Index )
- 장) 훨씬 적은 공간을 사용
- 단) 주어진 record의 key를 찾는데 더 많은 시간 걸림
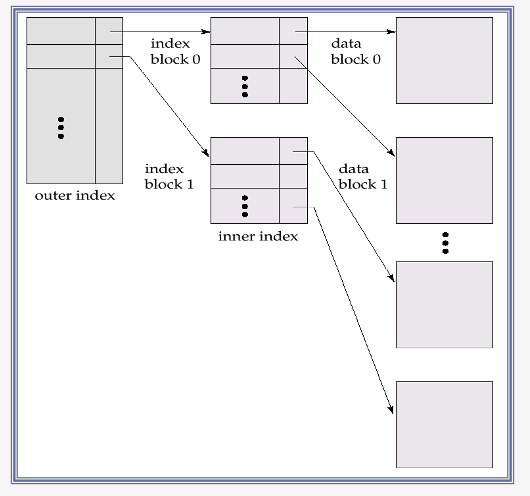
Primary Index : Multilevel Index Files
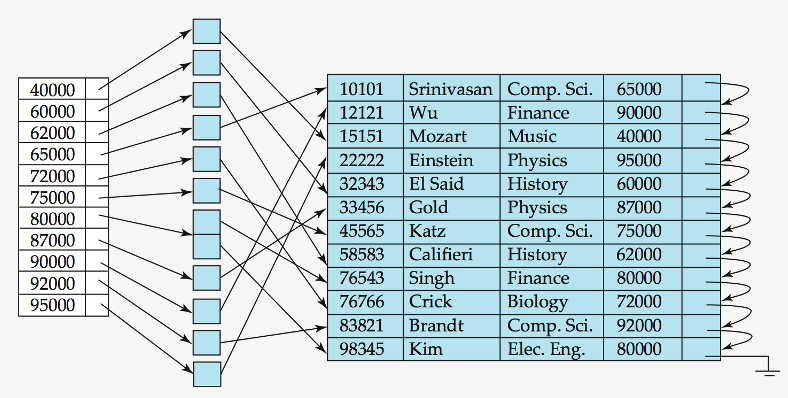
Secondary Index
(3) B\(^{+}\)-Tree Index Files
( = alternative to indexed-sequential files )
Indexed-sequential files의 단점
-
Performance degrades as file grows
( many overflow blocks get created for index files )
-
Periodic reorganization of entire index file is required
B\(^{+}\)-Tree Index Files의 장점
- automatically reorganizes itself with small and local changes
- Reorganization of entire file is not required to maintain performance
B\(^{+}\)-Tree Index Files의 단점
- extra insertion and deletion overhead, space overhead
B\(^{+}\)-Tree Index Files의 특징
- All paths from root to leaf are of the same length
- Each node that is not a root or a leaf has between \(\lceil\mathrm{n} / 2\rceil\) and \(n\) children
- A leaf node that is not a root has between \(n\lceil(n-1) / 2\rceil\) and \(n-1\) values
- Root must have at least two children
Node의 구조

- \(K_i\) : search-key
- \(P_i\) : pointers …
- to children ( for non-leaf nodes )
- to records ( for leaf nodes )
- \(K_i\)s in a node are ordered as…
- \(K_1 < \cdots K_{n-1}\).
Leaf Nodes
- ( For \(i\) = 1, 2, …, n-1 ) \(P_i\) either points to …
- (1) a file record with \(K_i\)
- (2) a bucket of pointers to file records
- ( \(L_i\) : leaf node \(i\) ) if \(i < j\) , \(L_i\)’s search-key < \(L_j\)’s search-key
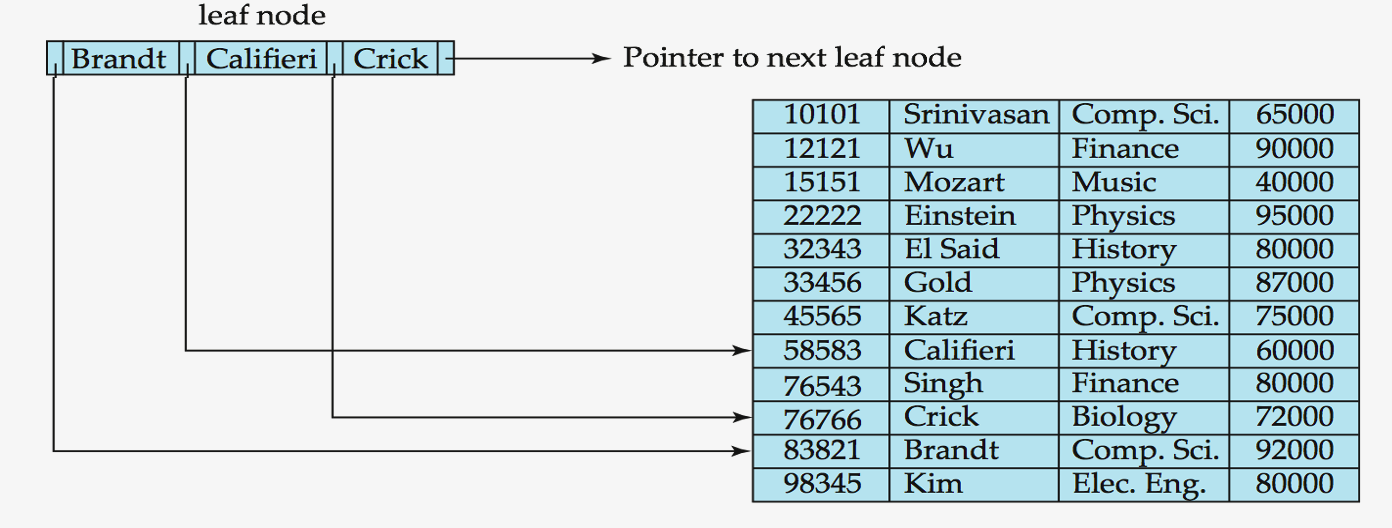
Non-Leaf Nodes
-
form a multi-level sparse index on the leaf nodes.
-
For a non-leaf node with \(m\) pointers …
- (1) All the search-keys in the subtree to which \(P_1\) points < \(K_1\)
-
(2) All the search-keys in the subtree to which \(P_m\) points \(\geq\) \(K_{m-1}\)
- (3) ( For \(2 \leq i \leq m-1\) )
- \(K_{i-1}\) \(\leq\) All the search-keys in the subtree to which \(P_i\) points <\(K_{i}\)
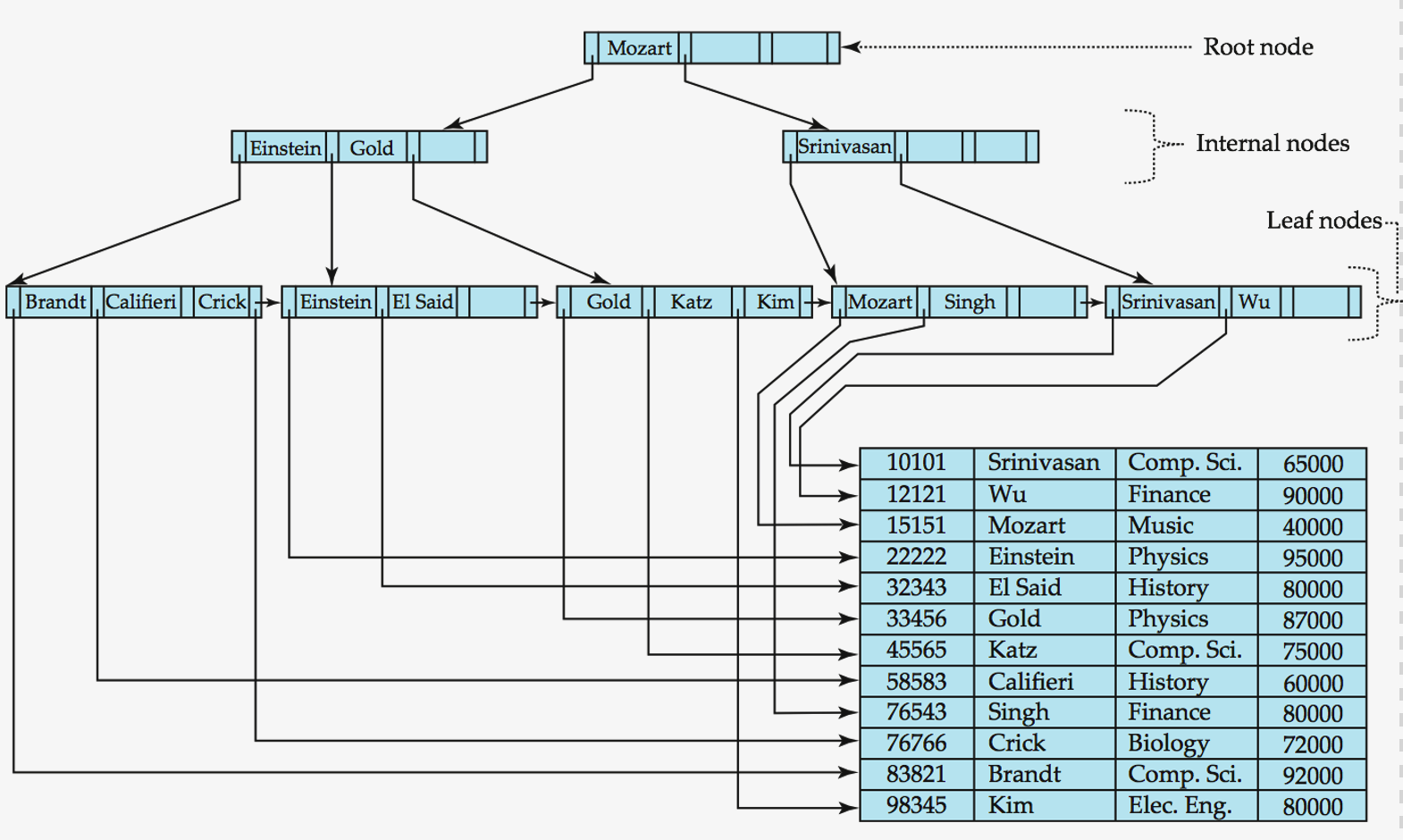
Queries On B\(^+\)-Trees

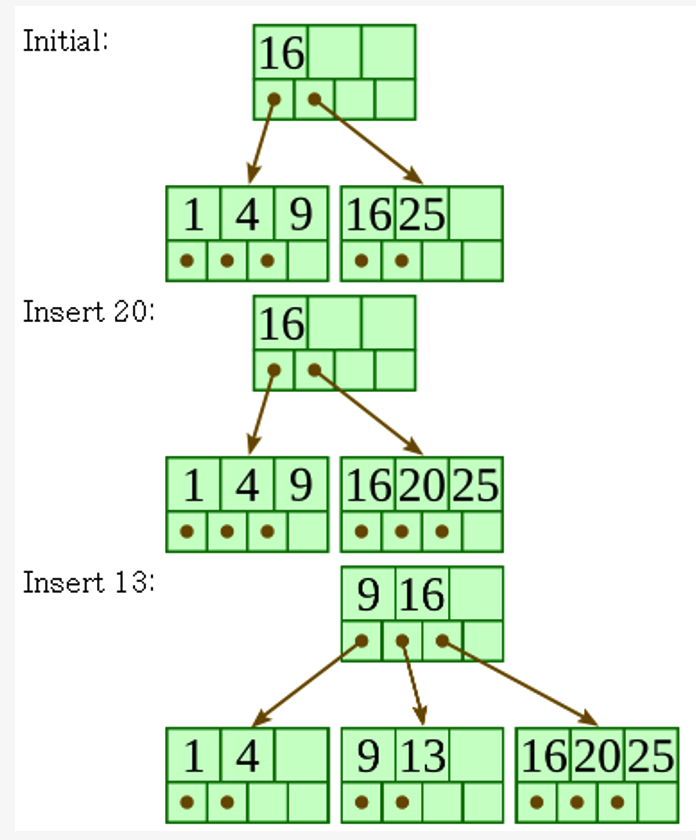
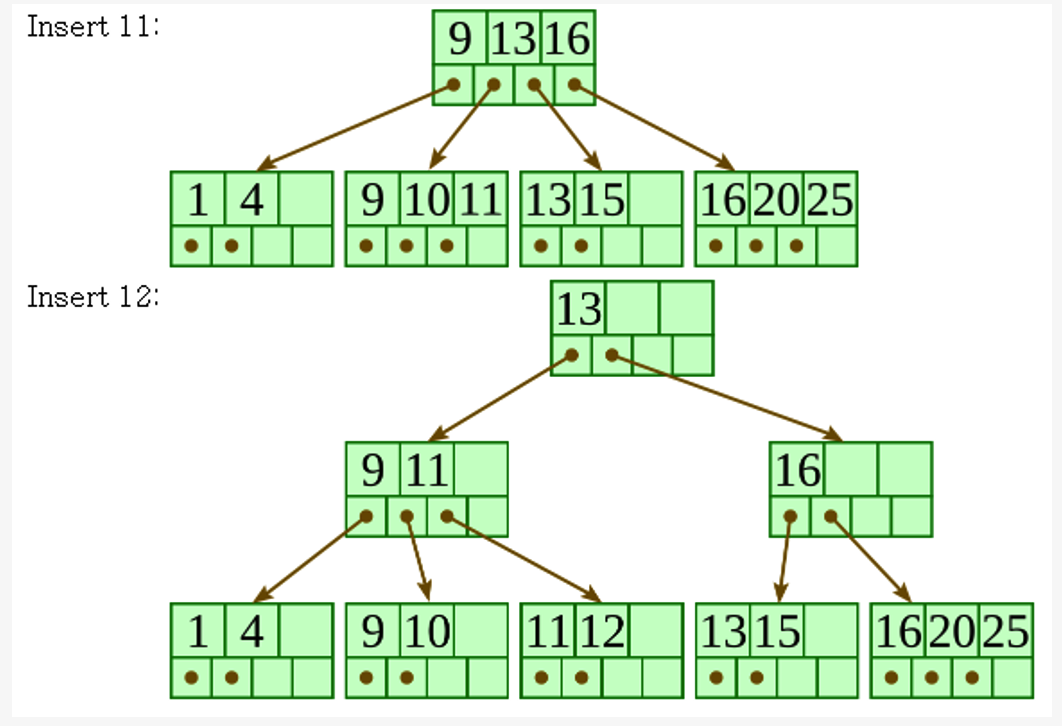
B\(^+\)-Tree Insertion
- filled from bottom
- Perform a search to find a target leaf node for the new entry
- (a) if the leaf node is NOT FULL
- add the entry
- (b) if the leaf node is FULL
- b-1) split the node into 2 parts
- b-2)
- 1st half entries are stored in one node
- 2nd half entries are moved to a new node
- b-3) The first entry of a new node is copied to the parent of the leaf
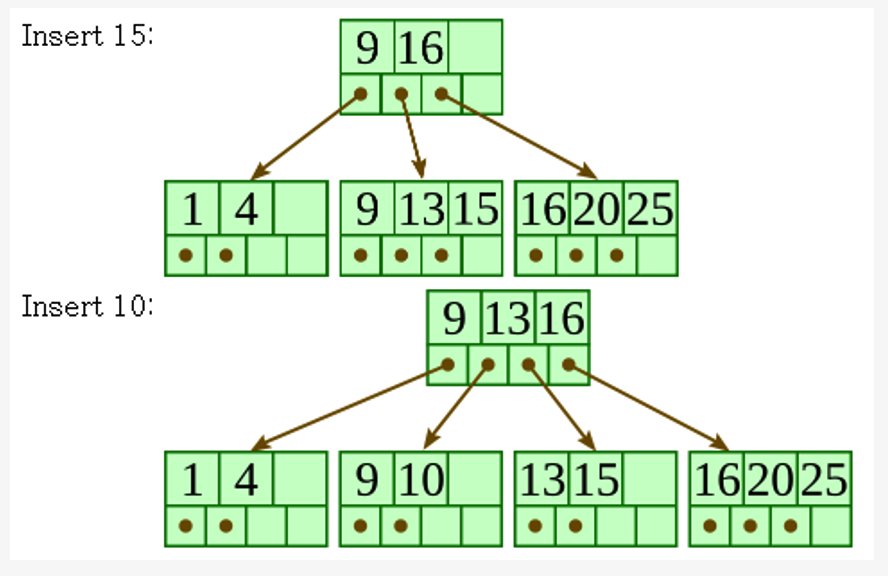
- (a) if the leaf node is NOT FULL
- If a non-leaf node overflows:
- b-1) SAME
- b-2) SAME
- b-3) The first entry of a new node is moved to the parent of the node
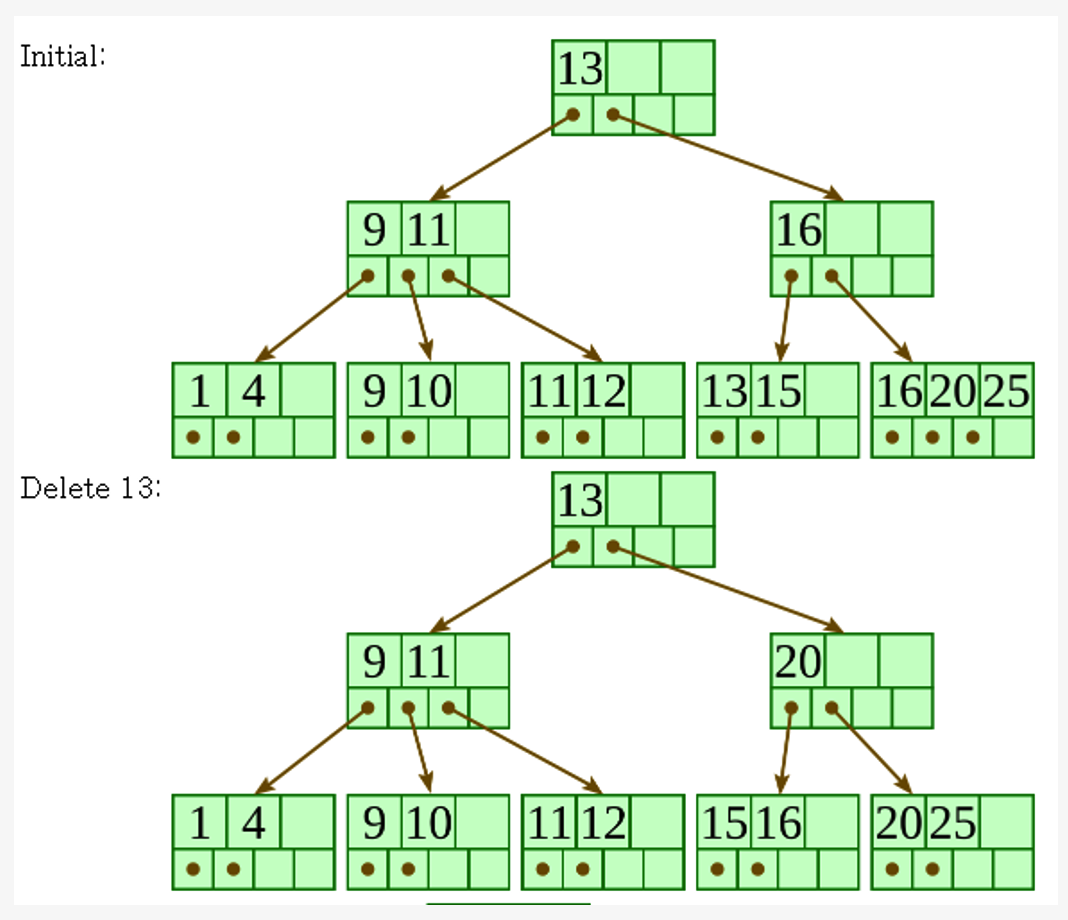
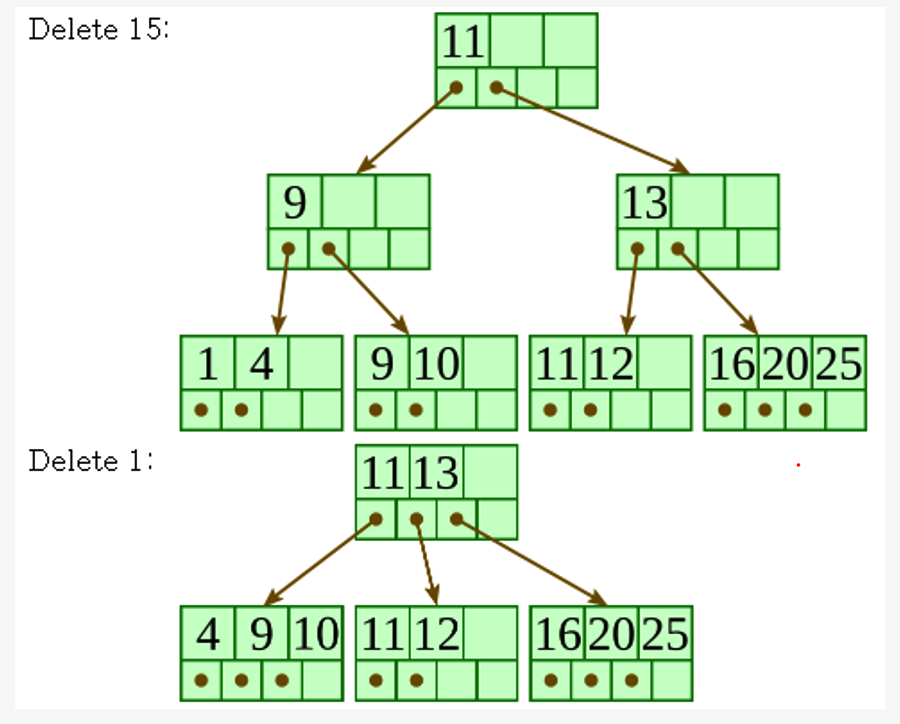
B\(^+\)-Tree Deletion
-
The target entry is searched &deleted at the leaf node
-
If underflow occurs after deletion,
\(\rightarrow\) distribute the entries from the node left to it
-
If distribution is not possible from left,
\(\rightarrow\) distribute from the node right to it
-
If distribution is not possible from left or from right,
\(\rightarrow\) merge the node with left and right to it
(4) B-Tree Index Files
B-Tree vs B\(^+\)-Tree
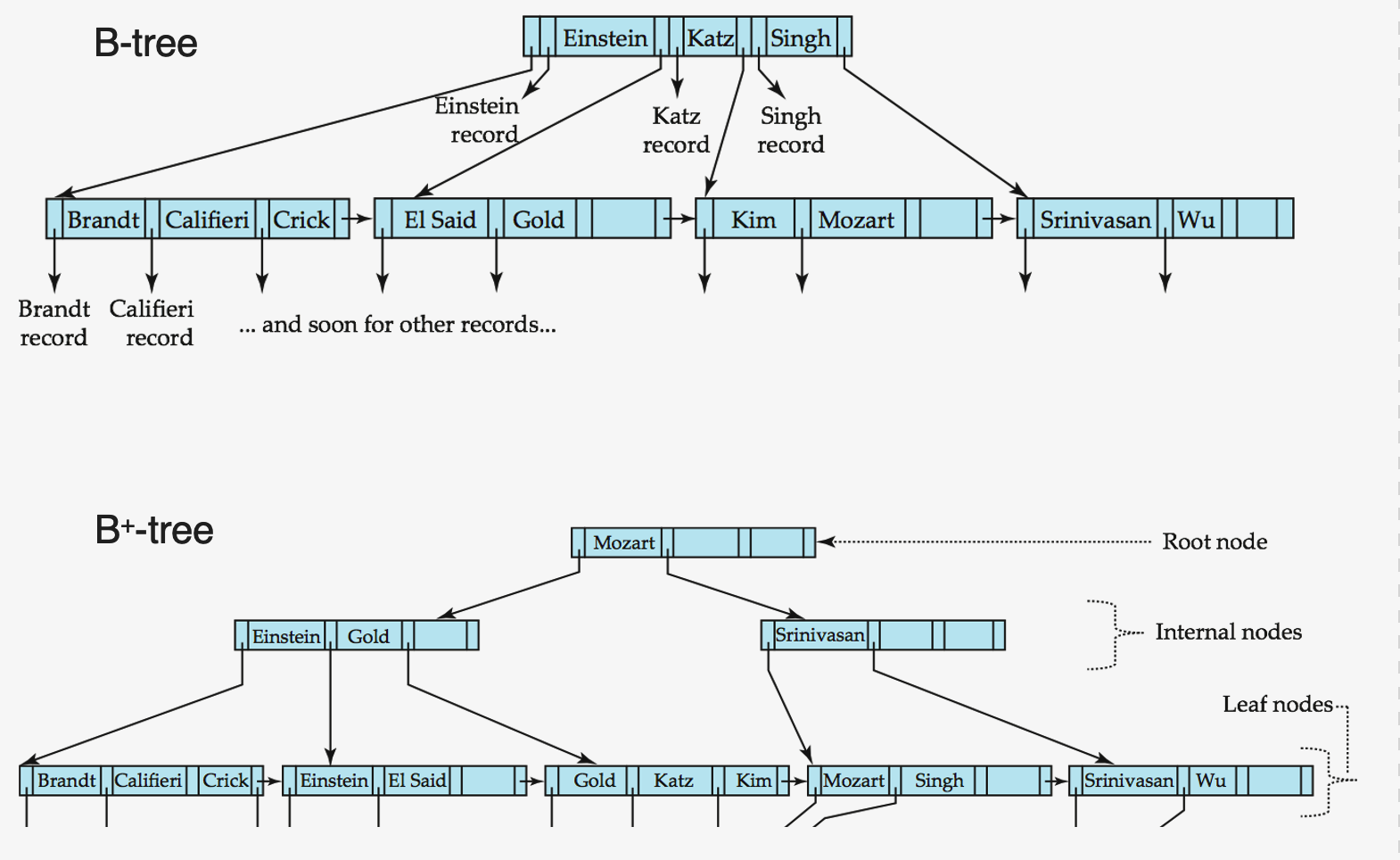
Details
-
allows search-key values to appear only once
( = eliminates redundant storage of search keys )
-
search keys in non-leaf nodes appear no where else in the B-tree
- an additional pointer field for each search key in a non-leaf node must be included
Advantages of B-Tree indices:
-
use less tree nodes than a corresponding B+-Tree
-
Sometimes possible to find search-key value before reaching leaf node
Disadvantages of B-Tree indices:
-
Non-leaf nodes are larger ( keeps data in it )
-> typically have greater depth than corresponding B+-Tree
-
Insertion and deletion more complicated than in B+-Trees
-
Implementation is harder than B+-Trees
