Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

An Overview of Deep Semi-Supervised Learning (2020) - Part 3


Contents

  1. Abstract
  2. Introduction
    1. SSL
    2. SSL Methods
    3. Main Assumptions in SSL
    4. Related Problems
  3. Consistency Regularization
    1. Ladder Networks
    2. Pi-Model
    3. Temporal Ensembling
    4. Mean Teachers
    5. Dual Students
    6. Fast-SWA
    7. Virtual Adversarial Training (VAT)
    8. Adversarial Dropout (AdD)
    9. Interpolation Consistency Training (ICT)
    10. Unsupervised Data Augmentation
  4. Entropy Minimization
  5. Proxy-label Methods
    1. Self-training
    2. Multi-view Training
  6. Holistic Methods
    1. MixMatch
    2. ReMixMatch
    3. FixMatch
  7. Generative Models
    1. VAE for SSL
    2. GAN for SSL
  8. Graph-Based SSL
    1. Graph Construction
    2. Label Propagation
  9. Self-Supervision for SSL


6. Generative Models

Unsupervised Learning

  • provided with \(x \sim p(x)\)
  • objective : estimate the density


Supervised Learning

  • objective : find the relationship between \(x\) & \(y\)

    • minimizing the functional \(p(x, y)\)

  • interested in the conditional distributions \(p(y \mid x)\),

    ( without the need to estimate \(p(x)\) )


Semi-supervised Learning with generative models

  • extension of supervised / unsupervised learning
    • information about \(p(x)\) provided by \(\mathcal{D}_u\)
    • information of the provided labels from \(\mathcal{D}_l\)


(1) VAE for SSL

standard VAE

  • autoencoder trained with a reconstruction loss
  • + variational objective term
    • attempts to learn a latent space that roughly follows a unit Gaussian distribution,
    • implemented as the KL-divergence between latent space & standard Gaussian


Notation :

  • input : \(x\)
  • encoder : \(q_\phi(z \mid x)\)
  • standard Gaussian distn : \(p(z)\)
  • reconstructed input : \(\hat{x}\)
  • decoder : \(p_\theta(x \mid z)\)


Loss Function :

  • \(\mathcal{L}=d_{\mathrm{MSE}}(x, \hat{x})+d_{\mathrm{KL}}\left(q_\phi(z \mid x), p(z)\right)\).


a-1) Standard VAEs for SSL (M1 Model)

  • consists of an unsupervised pretraining stage
  • step 1) pre-train
    • VAE is trained using the labeled and unlabeled examples
  • step 2) standard supervised task
    • 2-1) transform input \(x\)
      • \(x \in \mathcal{D}_l\) are transformed into \(z\)
    • 2-2) supervised task : \((z, y)\)
  • pros : classification can be performed in a lower dim


a-2) Extending VAEs for SSL (M2 Model)

  • limitation of M1 model :
    • labels of \(\mathcal{D}_l\) were ignored when training the VAE
  • M2 model : also use label info
  • 3 components
    • (1) classification network : \(q_\phi(y \mid x)\)
    • (2) encoder : \(q_\phi(z \mid y, x)\)
    • (3) decoder : \(p_\theta(x \mid y, z)\)
  • similar to a standard VAE …
    • with the addition of the posterior on \(y\)
    • loss terms to train \(q_\phi(y \mid x)\) if the labels are available
  • \(q_\phi(y \mid x)\) : can then be used at test time to get the predictions on unseen data


a-3) Stacked VAEs (M1+M2 Model)

  • concatenate M1 & M2
  • procedures
    • step 1) M1 is trained to obtain the \(z_1\)
    • step 2) M2 uses the \(z_1\) from model M1 , instead of raw \(x\)
  • final model :
    • \(p_\theta\left(x, y, z_1, z_2\right)=p(y) p\left(z_2\right) p_\theta\left(z_1 \mid y, z_2\right) p_\theta\left(x \mid z_1\right)\).


b) Variational Auxiliary Autoencoder

extends the variational distn with auxiliary variables \(a\)

  • \(q(a, z \mid x)=q(z \mid a, x) q(a \mid x)\).

pros : marginal distribution \(q(z \mid x)\) can fit more complicated posteriors \(p(z \mid x)\)


to have an unchanged generative model \(p(x \mid z)\)….

  • joint mode \(p(x,z,a)\) gives back the original \(p(x,z)\) under marginalization over \(a\)

    \(\rightarrow\) \(p(x,z,a) = p(a \mid x,z)p(x,z)\) , with \(p(a \mid x, z) \neq p(a)\)


SSL setting : use class information

  • additional latent variable \(y\) is introduced
  • generative model : \(p(y) p(z) p(a \mid z, y, x) p(x \mid y, z)\)
    • \(a\) : auxiliary variable
    • \(y\) : class label
    • \(z\) : latent features
  • result : 5 NNs
    • (1) auxiliary inference model : \(q(a \mid x)\)
    • (2) latent inference model : \(q(z \mid a, y, x)\)
    • (3) classifiaciton model : \(q(y \mid a, x)\)
    • (4) generative model 1 : \(p(a \mid \cdot)\)
    • (5) generative model 2 : \(p(x \mid \cdot)\)


(2) GAN for SSL

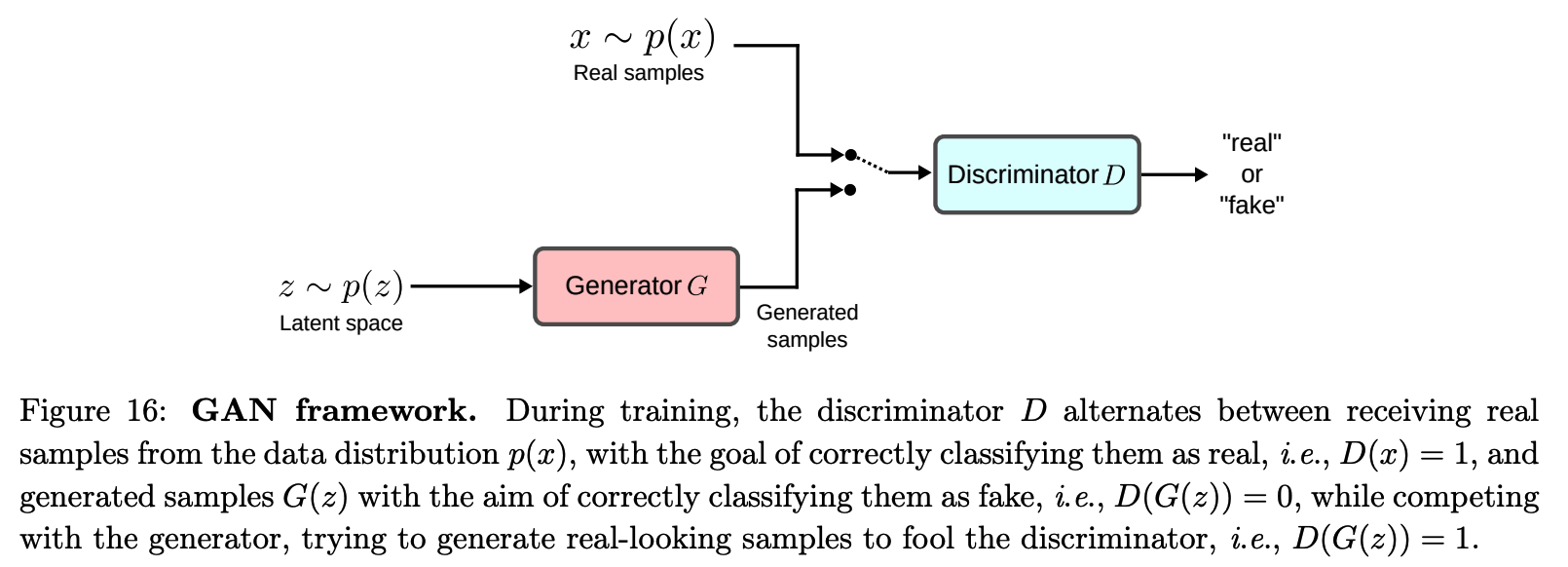
figure2

\(\begin{aligned} \mathcal{L}_D &=\max _D \mathbb{E}_{x \sim p(x)}[\log D(x)]+\mathbb{E}_{z \sim p(z)}[1-\log D(G(z))] \\ \mathcal{L}_G &=\min _G-\mathbb{E}_{z \sim p(z)}[\log D(G(z))] \end{aligned}\).


a) CatGAN (Categorical GAN)

GAN vs CatGAN

  • GAN : real vs fake
  • CatGAN : class 1 vs class2 vs … class K vs fake


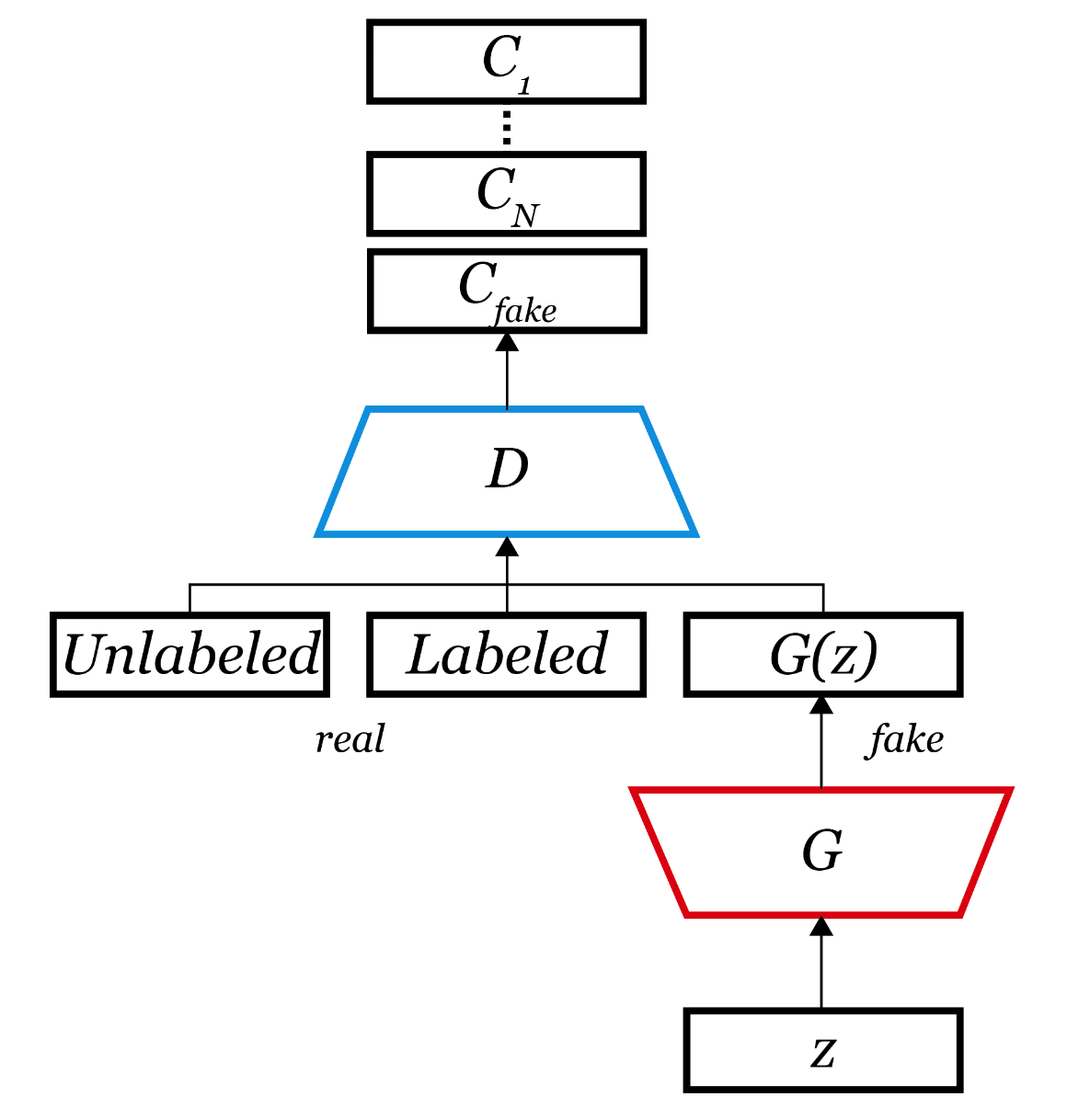
figure2

combining both the generative & discriminative perspectives

  • discriminator \(D\) plays the role of \(C\) classifiers


Objective :

  • trained to maximize the mutual information between…
    • (1) the inputs \(x\)
    • (2) predicted labels for a number of \(C\) unknown classes


For Discriminator….

  • real data : one class label \(\rightarrow\) minimize \(H[p(y \mid x, D)]\)

  • fake data : no class \(\rightarrow\) maximize \(H[p(y\mid x, G(z))]\)

  • assumption that # of data of each class are even :

    \(\rightarrow\) maximize \(H[p(y \mid D)]\)


For Generator ….

  • have to fool Discriminator that generated data belongs to certain class

    \(\rightarrow\) minimize \(H[p(y\mid x, G(z))]\)

  • assumption that # of data of each class are even :

    \(\rightarrow\) maximize \(H[p(y \mid D)]\)


Loss Function

\(\begin{aligned} \mathcal{L}_D &=\max _D-\mathbb{E}_{x \sim p(x)}[\mathrm{H}(D(x))]+\mathbb{E}_{z \sim p(z)}[\mathrm{H}(D(G(z)))]+\mathrm{H}_{\mathcal{D}} \\ \mathcal{L}_G &=\min _G \mathbb{E}_{z \sim p(z)}[\mathrm{H}(D(G(z)))]-\mathrm{H}_G \end{aligned}\).

  • \(\mathrm{H}_{\mathcal{D}} =\mathrm{H}\left(\frac{1}{N} \sum_{i=1}^N D\left(x_i\right)\right)\).
  • \(\mathrm{H}_G \approx \mathrm{H}\left(\frac{1}{M} \sum_{i=1}^M D\left(G\left(z_i\right)\right)\right)\).


SSL setting

  • \(x\) comes from \(\mathcal{D}_l\)
  • \(y\) comes in form of one-hot vector


Loss function of \(D\) :

  • \(\mathcal{L}_D+\lambda \mathbb{E}_{(x, y) \sim p(x)_{\ell}}[-y \log G(x)]\).


b) DCGAN

build good image representations by training GANs

\(\rightarrow\) reuse parts of the \(G\) & \(D\) as feature extractors for supervised tasks


c) SGAN (Semi-Supervised GAN)

DCGAN : \(D\) & \(G\) improves alternatively

SGAN : does it simultaneously!

  • instead of real/fake discrimination, has \(C+1\) outputs!

    ( sigmoid \(\rightarrow\) softmax )

  • architecture : same as DCGAN


d) Feature Matching GAN

Feature Matching

  • Instead of directly maximizing the output of the discriminator…

​ \(\rightarrow\) requires the \(G\) to generate data that matches the first-order feature statistics between of the data distribution


Example ) intermediate layer :

  • \(\mid \mid \mathbb{E}_{x \sim p(x)}[h(x)]-\mathbb{E}_{z \sim p(z)}[h(G(z))] \mid \mid ^2\).


Still have the problem of generator mode collapse!

\(\rightarrow\) minibatch discrimination

( = allow the discriminator to look at multiple data examples in combination )


SSL settings

  • \(D\) in feature matching GAN employs a \((C+1)\)-classification ( instead of binary classification )
  • the prob of \(x\) being fake : \(p(y=C+1 \mid G(z), D)\)
    • ( = \(1-D(x)\) in the original GAN )
  • Loss function : \(\mathcal{L}=\mathcal{L}_s+\mathcal{L}_u\)
    • \(\mathcal{L}_s =-\mathbb{E}_{x, y \sim p(x)_l}[\log p(y \mid x, y<K+1, D)]\).
    • \(\mathcal{L}_u =-\mathbb{E}_{x \sim p(x)_u} \log \ [1-p(y=K+1 \mid x, D)]-\mathbb{E}_{z \sim p(z)} \log \ [p(y=K+1 \mid G(z), D))]\).


e) Bad GAN


f) Triple-GAN


g) BiGAN


Categories:

Updated:

You May Also Enjoy

less than 1 minute read

2 minute read

4 minute read

1 minute read