(paper) SSL08 - MixMatch

MixMatch: A Holistic Approach to Semi-Supervised Learning (2019)

Contents

1. Abstract
2. Related works
   1. Consistency Regularization
   2. Entropy Minimization
   3. Traditional Regularization
3. MixMatch
   1. Data Augmentation
   2. Label Guessing
   3. Mixup
   4. Pseudo Code

0. Abstract

MixMatch = (1) + (2) + (3)

• unification of current dominant approaches for SSL
• guesses low-entropy labels for data-augmented unlabeled data
• mixes labeled & unlabeled data using MixUp

1. Related works

existing methods for SSL

(1) Consistency Regularization

applies input transformations assumed to leave class semantics unaffected

• ex) deform or add noise to an input image, without altering label

Application to SSL :

• classifier should output the same class distribution for an unlabeled example,

  even after it has been augmented

• enforces \(x\) should be classified the same as \(\text{Augment}(x)\)

Add the loss term :

• \(\mid \mid \mathrm{p}_{\text {model }}(y \mid \operatorname{Augment}(x) ; \theta)-\mathrm{p}_{\text {model }}(y \mid \operatorname{Augment}(x) ; \theta) \mid \mid _2^2\).

Drawback of this approach : domain-specific DA

\(\rightarrow\) (solution) VAT : compute an additive perturbation to apply to the input which maximally changes the output class distn

MixMatch : use consistency regularization through the use of standard data augmentation for images

• ex) random horizontal flips & crops

(2) Entropy Minimization

require that the classifier output low-entropy predictions on unlabeled data

Pseudo-Label

• does entropy minimization implicitly, by constructing hard labels with high-confidence predictions ( treat them as training data )

(3) Traditional Regularization

constraint on a model to make it harder to memorize the training data

\(\rightarrow\) make it generalize better to unseen data

2. MixMatch

“holistic” approach

• incorporates ideas from the previous works ( in section 1 )

Notation :

• \(\mathcal{X}\) : labeled examples ( with one of \(L\) labels )

• \(\mathcal{U}\) : unlabeled examples

  ( \(\mathcal{X}\) & \(\mathcal{U}\) : equally-sized batch )

MixMatch produces ….

• augmented labeled examples \(\mathcal{X}^{\prime}\)
• augmented unlabeled examples with “guessed” labels \(\mathcal{U}^{\prime}\)

Combined Loss function :

• \(\mathcal{X}^{\prime}, \mathcal{U}^{\prime} =\operatorname{MixMatch}(\mathcal{X}, \mathcal{U}, T, K, \alpha)\).
• \[\mathcal{L} =\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}} \mathcal{L}_{\mathcal{U}}\]
  • \(\mathcal{L}_{\mathcal{X}} =\frac{1}{ \mid \mathcal{X}^{\prime} \mid } \sum_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}\left(p, \mathrm{p}_{\text {model }}(y \mid x ; \theta)\right)\).
  • \(\mathcal{L}_{\mathcal{U}} =\frac{1}{L \mid \mathcal{U}^{\prime} \mid } \sum_{u, q \in \mathcal{U}^{\prime}} \mid \mid q-\operatorname{p}_{\text {model }}(y \mid u ; \theta) \mid \mid _2^2\).
• \(\mathrm{H}(p, q)\) : cross-entropy between \(p\) & \(q\)

(1) Data Augmentation

For each \(x_b\) in \(\mathcal{X}\) … \(1\) DA

\(\rightarrow\) \(\hat{x}_b=\operatorname{Augment}\left(x_b\right)\)

For each \(u_b\) in \(\mathcal{U}\) … \(K\) DA

\(\rightarrow\) \(\hat{u}_{b, k}=\operatorname{Augment}\left(u_b\right)\) , where \(\left(u_b\right), k \in(1, \ldots, K)\)

use these augmentations to generate a “guessed label” \(q_b\) for each \(u_b\)

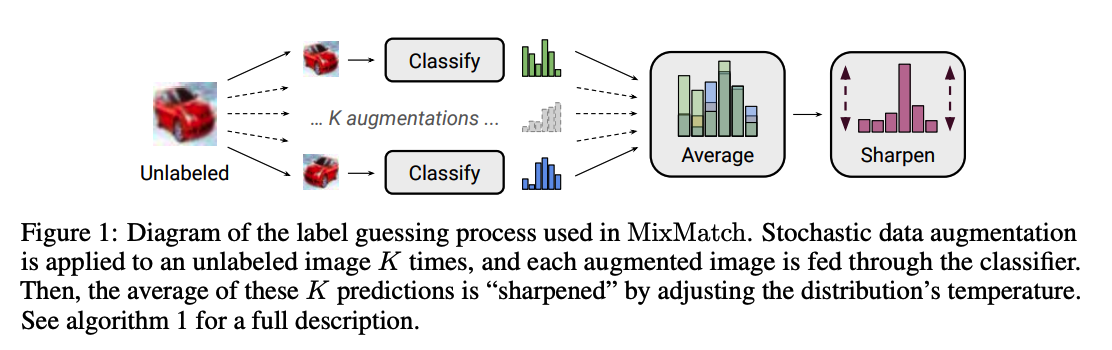
(2) Label Guessing

For each unlabeled example in \(\mathcal{U}\)…

\(\rightarrow\) produce a guess label, based on model prediction

\(\bar{q}_b=\frac{1}{K} \sum_{b=1}^K \operatorname{p}_{\operatorname{model}}\left(y \mid \hat{u}_{b, k} ; \theta\right)\).

Sharpening

when generating label guess, one additional step!

( motivated by entropy minimization )

Given \(\bar{q}_b\), apply a sharpening function to reduce the entropy of the label distn

\(\operatorname{Sharpen}(p, T)_i:=p_i^{\frac{1}{T}} / \sum_{j=1}^L p_j^{\frac{1}{T}}\).

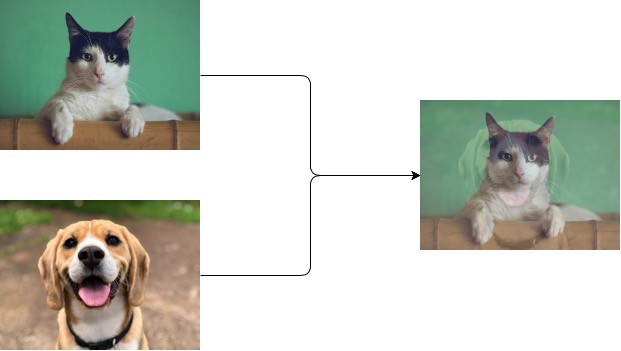
(3) MixUp

(4) Pseudo Code