(paper 100) Non-stationary Transformers:Exploring the Stationarity in Time Series Forecasting

Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting (NeurIPS 2022)

https://github.com/thuml/Nonstationary_Transformers.

Contents

1. Abstract
2. Introduction
3. Related Works
   1. Deep Models for TSF
   2. Stationarization for TSF
4. Non-stationary Transformers
   1. Series Stantionarization
   2. De-stationary Attention
5. Experiments
   1. Experimental Setups
   2. Main Results
   3. Ablation Study

Abstract

Previous studies : use stationarization to attenuate the non-stationarity of TS

\(\rightarrow\) can be less instructive for real-world TS

Non-stationary Transformers

Two interdependent modules:

• (1) Series Stationarization
  • unifies the statistics of each input
  • converts the output with restored statistics
• (2) De-stationary Attention
  • to address over-stationarization problem
  • use attention to recover the intrinsic non-stationary information into temporal dependencies

1. Introduction

Non-stationarity of data

• continuous change of statistical properties and joint distribution over time ( makes it less predictable [6, 14] )
• generally acknowledged to pre-process the time series by stationarization [24, 27, 15]

However, non-stationarity is the inherent property

\(\rightarrow\) also good guidance for discovering temporal dependencies

Example) Figure 1

• ( Figure 1 (a) ) Transformers can capture distinct temporal dependencies from different series

• ( Figure 1 (b) ) Transformers trained on the stationarized series tend to generate indistinguishable attentions

  \(\rightarrow\) over-stationarization problem

  • unexpected side-effect … makes Transformers fail to capture eventful temporal dependencies

Key question:

• (1) how to attenuate TS non-stationarity towards better predictability
• (2) mitigate the over-stationarization problem?

Proposal:

• explore the effect of stationarization in TSF
• propose Non-stationary Transformers

Non-stationary Transformers

two interdependent modules:

• (1) Series Stationarization
  • to increase the predictability of nonstationary series
• (2) De-stationary Attention
  • to alleviate over-stationarization

a) Series Stationarization

• simple normalization strategy
• to unify the key statistics of each series without extra parameters

b) De-stationary Attention

• approximates the attention of unstationarized data
• compensates the intrinsic non-stationarity of raw series

2. Related Works

(1) Deep Models for TSF

• pass

(2) Stationarization for TSF

Adaptive Norm [24]

• applies z-score normalization for each series fragment by global statistics

DAIN [27]

• employs a nonlinear NN to adaptively stationarize TS

RevIN [15]

• two-stage instance normalization

Non-stationary Transformer

• directly stationarizing TS will damage the model’s capability of modeling specific temporal dependency.
• in addition to the (1) stationarization, further develops (2) De-stationary Attention to bring the intrinsic non-stationarity of the raw series back to attention.

3. Non-stationary Transformers

(1) Series Stationarization

Straightforward but effective design to wrap Transformers as the base model without extra parameters

2 corresponding operations:

• (1) Normalization module
• (2) De-normalization module

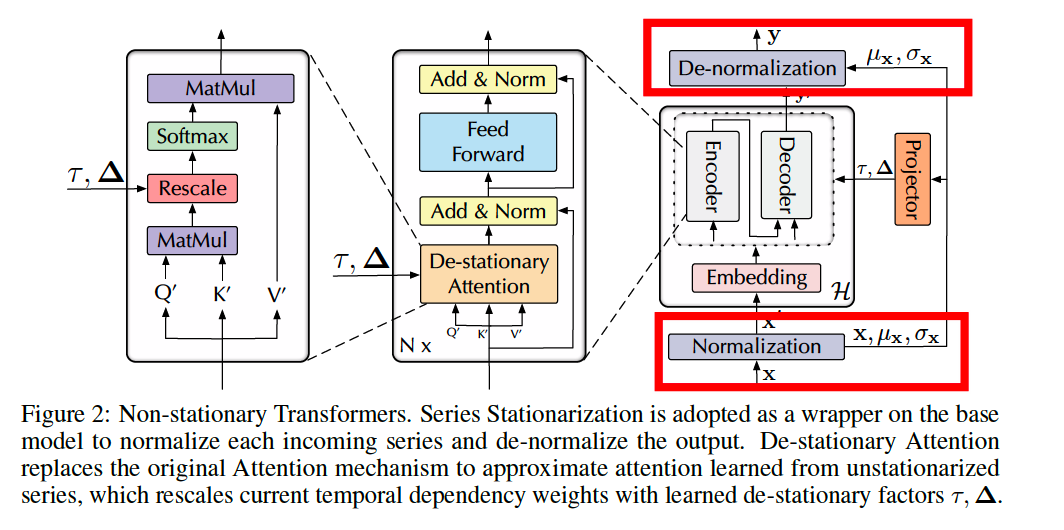
(2) De-stationary Attention

Non-stationarity of the original TS cannot be fully recovered only by Denormalization!

De-stationary Attention mechanism

• approximate the attention that is obtained without stationarization
• discover the particular temporal dependencies from original non-stationary TS

Self-Attention: \(\operatorname{Attn}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\mathbf{Q K}^{\top}}{\sqrt{d_k}}\right) \mathbf{V}\).

Bring the vanished non-stationary information back to its calculation

• approximate the

  • positive scaling scalar \(\tau=\sigma_{\mathbf{x}}^2 \in \mathbb{R}^{+}\)
  • shifting vector \(\boldsymbol{\Delta}=\mathbf{K} \mu_{\mathbf{Q}} \in \mathbb{R}^{S \times 1}\),

  which are defined as de-stationary factors.

• try to learn de-stationary factors directly from the statistics of unstationarized \(\mathbf{x}, \mathbf{Q}\) and \(\mathbf{K}\) by MLP

\(\log \tau=\operatorname{MLP}\left(\sigma_{\mathbf{x}}, \mathbf{x}\right)\).

\(\boldsymbol{\Delta}=\operatorname{MLP}\left(\mu_{\mathbf{x}}, \mathbf{x}\right)\). \(\operatorname{Attn}\left(\mathbf{Q}^{\prime}, \mathbf{K}^{\prime}, \mathbf{V}^{\prime}, \tau, \boldsymbol{\Delta}\right)=\operatorname{Softmax}\left(\frac{\tau \mathbf{Q}^{\prime} \mathbf{K}^{\prime}+\mathbf{1} \boldsymbol{\Delta}^{\top}}{\sqrt{d_k}}\right) \mathbf{V}^{\prime}\).

4. Experiments

(1) Experimental Setups

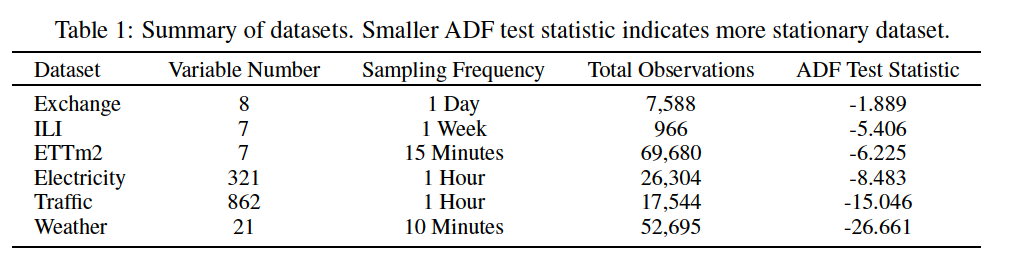
a) Datasets

• Electricity
• ETT datasets
• IExchange
• ILI
• Traffic
• Weather

b) Degree of stationarity

Augmented Dick-Fuller (ADF) test statistic

• small value = high stationarity

c) Baselines

• pass

(2) Main Results

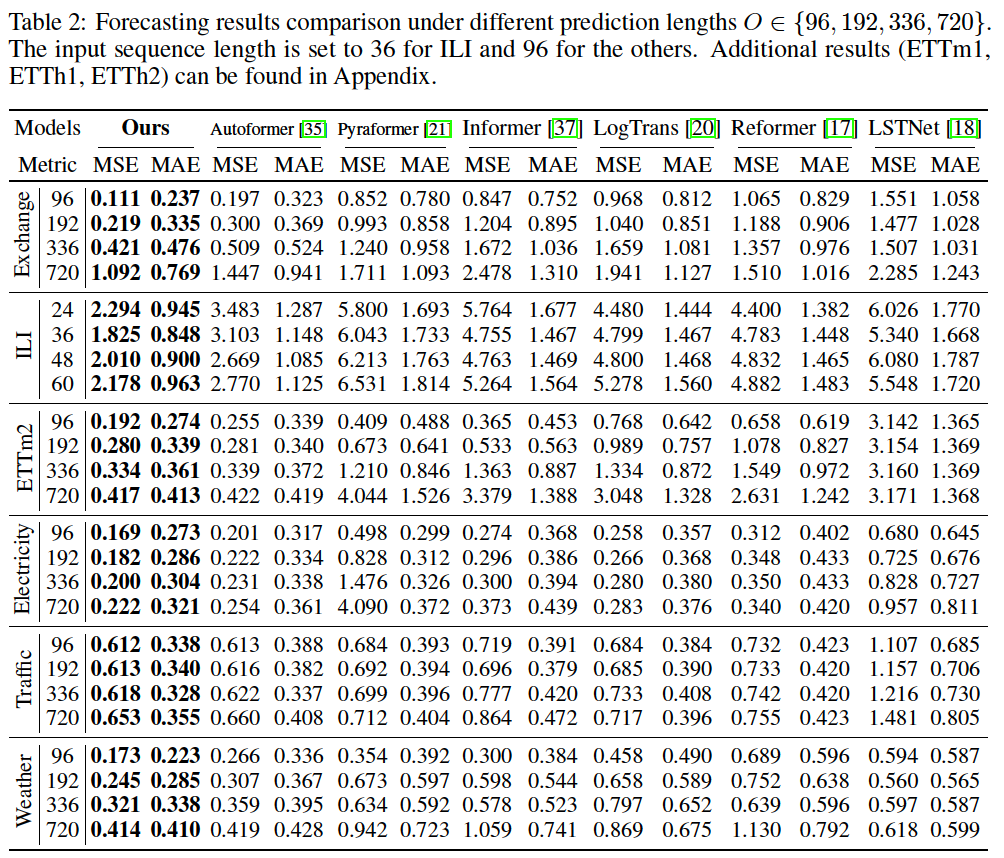
a) Forecasting

MTS Forecasting

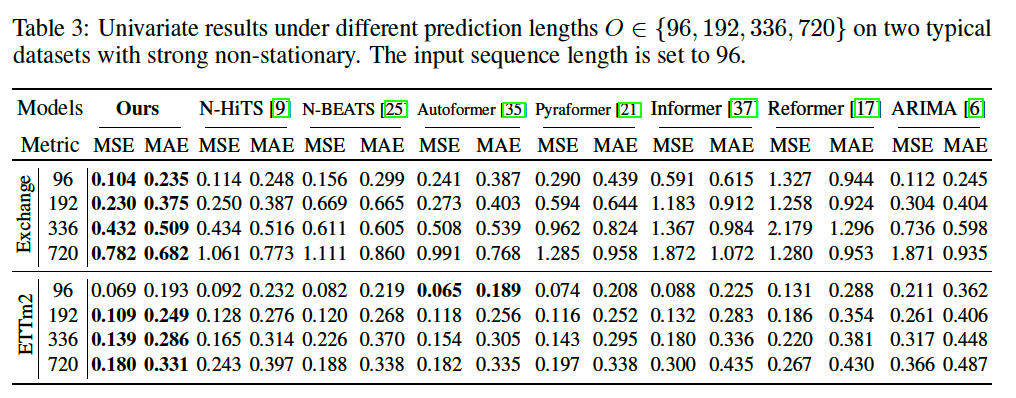
UTS Forecasting

b) Framework Generality

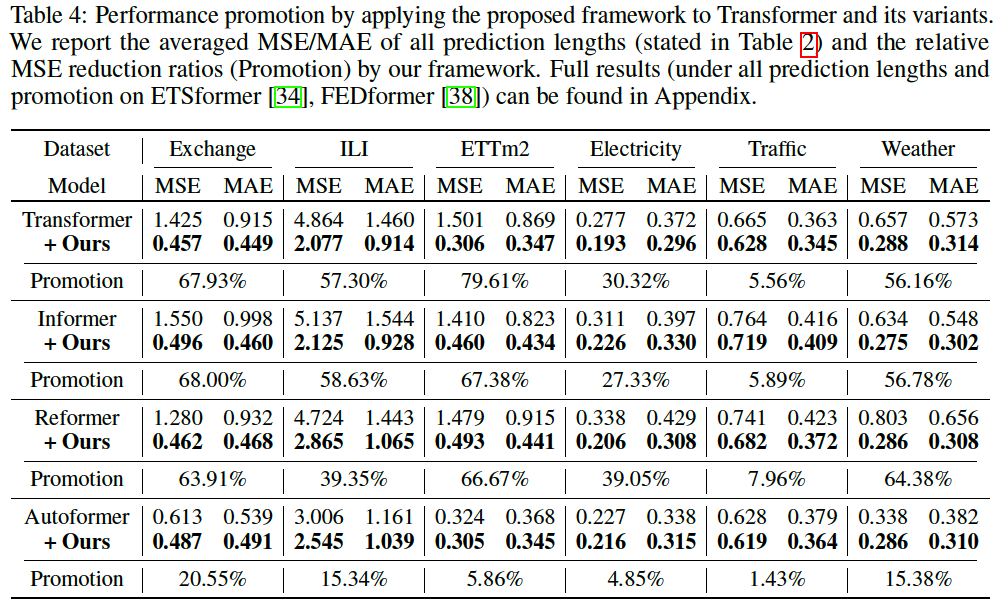
Conclusion: Non-stationary Transformer is an effective and lightweight framework that can be widely applied to Transformer-based models and enhances their non-stationary predictability

(3) Ablation Study

a) Quality evaluation

Dataset: ETTm2

Models:

• vanilla Transformer
• Transformer with only Series Stationarization
• Non-stationary Transformer

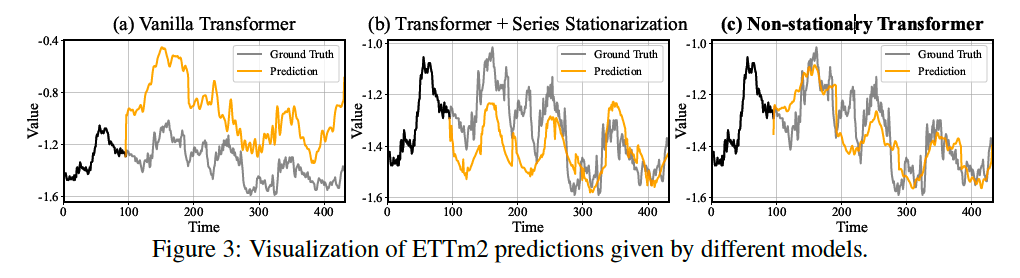
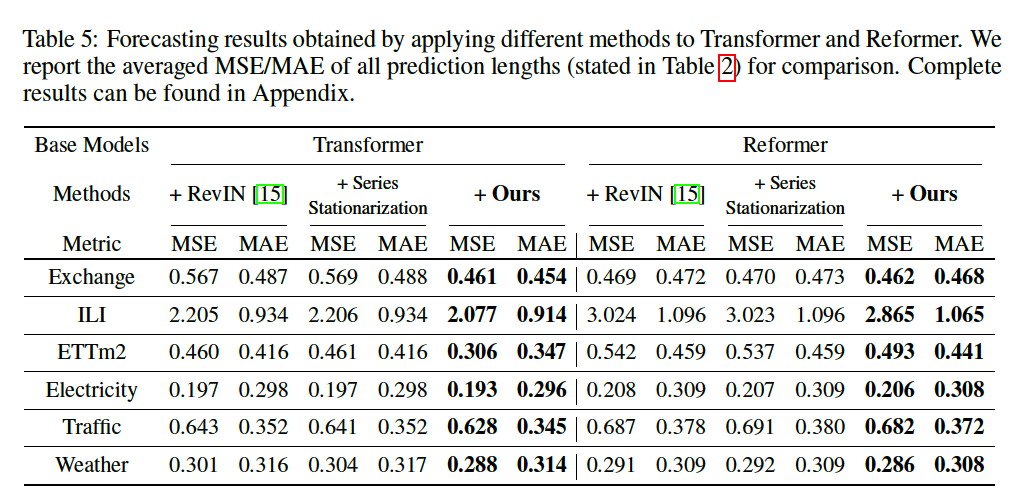
b) Quantitative performance

(3) Model Analysis

a) Over-stationarization problem

Transformers with ….

• v1) Transformer + Ours ( = Non-stationary Transformer )
• v2) Transformer + RevIN
• v3) Transformer + Series Stationarization

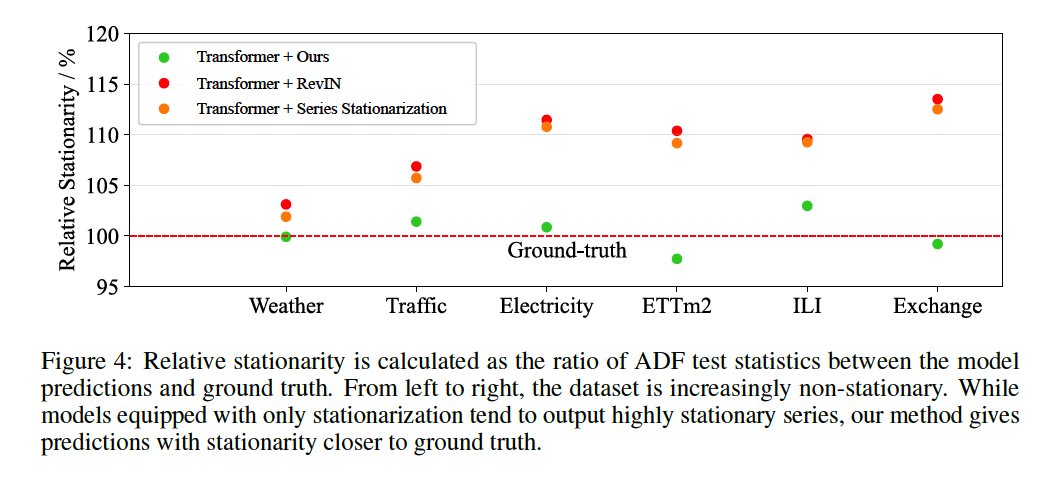
Result

• v2 & v3) tend to output series with unexpected high degree of stationarity