Are Transformers Effective for Time Series Forecasting?
Contents
- Abstract
- Introduction
- Preliminaries
- Transformoer-Based LTSF Solutions
- Embarassingly Simple Baseline
- Experiments
- Implementation Details
- LTSF & STSF
- Distribution Shift
0. Abstract
surge of Transformer-based solutions for the long-term time series forecasting (LTSF) task
\(\rightarrow\) this paper : question the validity of this line of research
Transformers : most successful solution to extract the semantic correlations among the elements in a long sequence.
However, in time series modeling, we are to extract the temporal relations in an ordered set of continuous points
[ Transformer ] positional encoding & tokens to embed sub-series
- facilitate preserving some ordering information….
\(\rightarrow\) BUT the nature of the permutation-invariant self-attention mechanism inevitably results in temporal information loss
\(\rightarrow\) introduce a set of embarrassingly simple one-layer linear models named LTSF-Linear
https://github.com/cure-lab/LTSFLinear.
1. Introduction
The main working power of Transformers: multi-head self-attention mechanism
\(\rightarrow\) capability of extracting semantic correlations among elements in a long sequence
Problems of self-attention in TS :
permutation invariant & “anti-order” to some extent
-
using various types of positional encoding…? still inevitable to have temporal information loss
( NLP : not a serious concern for semantic rich applications )
( TS : usually a lack of semantics in the numerical data itself )
\(\rightarrow\) order itself plays the most crucial role
Q. Are Transformers really effective for long-term time series forecasting?
(non-Transformer) Baselines ( used in Transformer-based papers )
- perform autoregressive or iterated multi-step (IMS) forecasting
- suffer from significant error accumulation effects for the LTSF problem
\(\rightarrow\) We challenge Transformer-based LTSF solutions with direct multi-step (DMS) forecasting strategies to validate their real performance
Hypothesize that long-term forecasting is only feasible for those time series with a relatively clear trend and periodicity.
\(\rightarrow\) linear models can already extract such information!
\(\rightarrow\) introduce a set of embarrassingly simple model, LTSF-Linear
LTSF-Linear
- regresses historical time series with a one-layer linear model to forecast future time series directly.
- conduct extensive experiments on nine widely-used benchmark datasets
- show that LTSF-Linear outperforms existing complex Transformerbased models in all cases, and often by a large margin (20% ∼ 50%).
- existing Transformers : most of them fail to extract temporal relations from long sequences
- the forecasting errors are not reduced (sometimes even increased) with the increase of look-back window sizes.
- conduct various ablation studies on existing Transformer-based TSF solutions
2. Preliminaries: TSF Problem Formulation
Notation
-
number of variates : \(C\)
-
historical data : \(\mathcal{X}=\left\{X_1^t, \ldots, X_C^t\right\}_{t=1}^L\)
- lookback window size : \(L\)
- \(i_{t h}\) variate at the \(t_{t h}\) time step : \(X_i^t\)
TSF task: predict \(\hat{\mathcal{X}}=\left\{\hat{X}_1^t, \ldots, \hat{X}_C^t\right\}_{t=L+1}^{L+T}\)
- iterated multi-step (IMS) forecasting : learns a single-step forecaster & iteratively applies it
- direct multistep (DMS) forecasting : directly optimizes the multi-step forecasting objective
IMS vs DMS
- IMS ) have smaller variance thanks to the autoregressive estimation procedure
- DMS) less error accumulation effects.
\(\rightarrow\) IMS forecasting is preferable when ….
- (1) highly-accurate single-step forecaster
- (2) \(T\) is relatively small
\(\rightarrow\) DMS forecasting is preferable when ….
- (1) hard to obtain an unbiased single-step forecasting model
- (2) \(T\) is large.
3. Transformer-Based LTSF Solutions
Transformer-based models to LTSF problems?
Limitations
- (1) quadratic time/memory complexity
- (2) error accumulation by autoregressive decoder
- Informer : reduce complexity & DMS forecasting
- etc) xxformers…
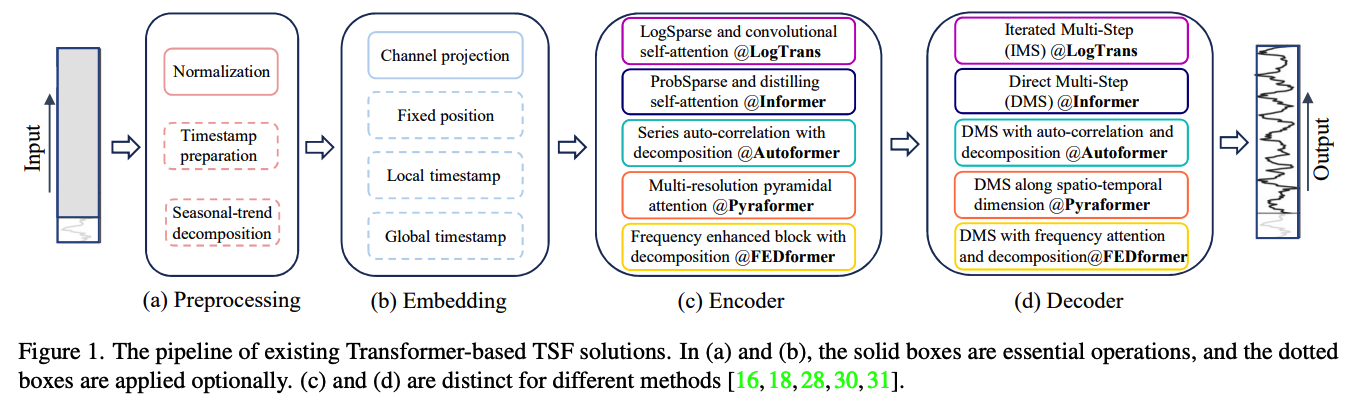
(1) TS decomposition
Common in TSF : normalization with zero-mean
Autoformer : applies seasonal-trend decomposition behind each neural block
- TREND : MA kernel on the input sequence to extract the TREND
- SEASONALITY : original - TREND
FEDformer : ( on top of Autoformer )
- proposes the mixture of experts’ strategies to mix the TREND components extracted by MA kernels with various kernel sizes.
(2) Input Embedding
self-attention layer : cannot preserve the positional information of the time series.
Local positional information ( i.e. the ordering of time series ) is important
Global temporal information ( such as hierarchical timestamps (week, month, year) and agnostic timestamps (holidays and events) ) is also informative
SOTA Transformer : inject several embeddings
- fixed positional encoding
- channel projection embedding
- learnable temporal embeddings
- temporal embeddings with a temporal convolution layer
- learnable timestamps
(3) Self-attention
Vanilla Transformer : \(O\left(L^2\right)\) ( too large )
Recent works propose two strategies for efficiency
- (1) LogTrans, Pyraformer
- explicitly introduce a sparsity bias into the self-attention scheme.
- ( LogTrans ) uses a Logsparse mask to reduce the computational complexity to \(O(\log L)\)
- ( Pyraformer ) adopts pyramidal attention that captures hierarchically multi-scale temporal dependencies with an \(O(L)\) time and memory complexity
- (2) Informer, FEDformer, Autoformer
- use the low-rank property in the self-attention matrix.
- ( Informer ) proposes a ProbSparse self-attention mechanism and a self-attention distilling operation to decrease the complexity to \(O(L \log L)\),
- ( FEDformer ) designs a Fourier enhanced block and a wavelet enhanced block with random selection to obtain \(O(L)\) complexity.
- (3) Autoformer
- designs a series-wise auto-correlation mechanism to replace the original self-attention layer.
(4) Decoders
Vanilla Transformer decoder
-
outputs sequences in an autoregressive manner
-
resulting in a slow inference speed and error accumulation effects
( especially for long-term predictions )
Use DMS strategies
-
Informer : designs a generative-style decoder for DMS forecasting.
- Pyraformer : uses a FC layer concatenating Spatio-temporal axes as the decoder.
- Autoformer : sums up two refined decomposed features from trend-cyclical components and the stacked auto-correlation mechanism for seasonal components to get the final prediction.
- FEDformer : uses a decomposition scheme with the proposed frequency attention block to decode the final results.
The premise of Transformer models : semantic correlations between paired elements
-
self-attention mechanism itself is permutation-invariant
\(\rightarrow\) capability of modeling temporal relations largely depends on positional encodings
-
there are hardly any point-wise semantic correlations between them
TS modeling
-
mainly interested in the temporal relations among a continuous set of points
& order of these elements ( instead of the paired relationship ) plays the most crucial role
-
positional encoding and using tokens :
- not sufficient! TEMPORAL INFORMATION LOSS!
\(\rightarrow\) Revisit the effectiveness of Transformer-based LTSF solutions.
4. An Embarrassingly Simple Baseline
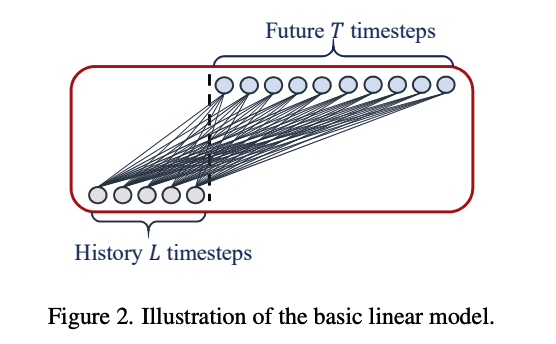
(1) Linear
LTSF-Linear: \(\hat{X}_i=W X_i\),
-
\(W \in \mathbb{R}^{T \times L}\) : linear layer along the temporal axis
-
\(\hat{X}_i\) and \(X_i\) : prediction and input for each \(i_{t h}\) variate
( LTSF-Linear shares weights across different variates & does not model any spatial correlations )
[Linear] Vanilla Linear : 1-layer Linear model
2 variantes :
- [DLinear] = Linear + Decomposition
- [NLinear] = Linear + Normalization
DLinear
( enhances the performance of a vanilla linear when there is a clear trend in the data. )
- step 1) decomposes a raw data input into a TREND & REMAINDER
- use MA kernel
- step 2) two 1-layer linear layer
- one for TREND
- one for REMAINDER
- step 3) sum TREND & REMAINDER
NLinear
( when there is a distribution shift )
- step 1) subtracts the input by the last value of the sequence
- step 2) one 1-layer linear layer
- step 3) add the subtracted value
5. Experiments
(1) Experimental Settings
a) Dataset
ETT (Electricity Transformer Temperature)
- ETTh1, ETTh2, ETTm1, ETTm2
Traffic, Electricity, Weather, ILI, ExchangeRate
\(\rightarrow\) all of them are MTS
b) Compared Methods
5 transformer based methods
- FEDformer, Autoformer, Informer, Pyraformer, LogTrans
naive DMS method:
- Closest Repeat (Repeat)
( two variants of FEDformer )
- compare with the better accuracy, FEDformer-f via Fourier Transform
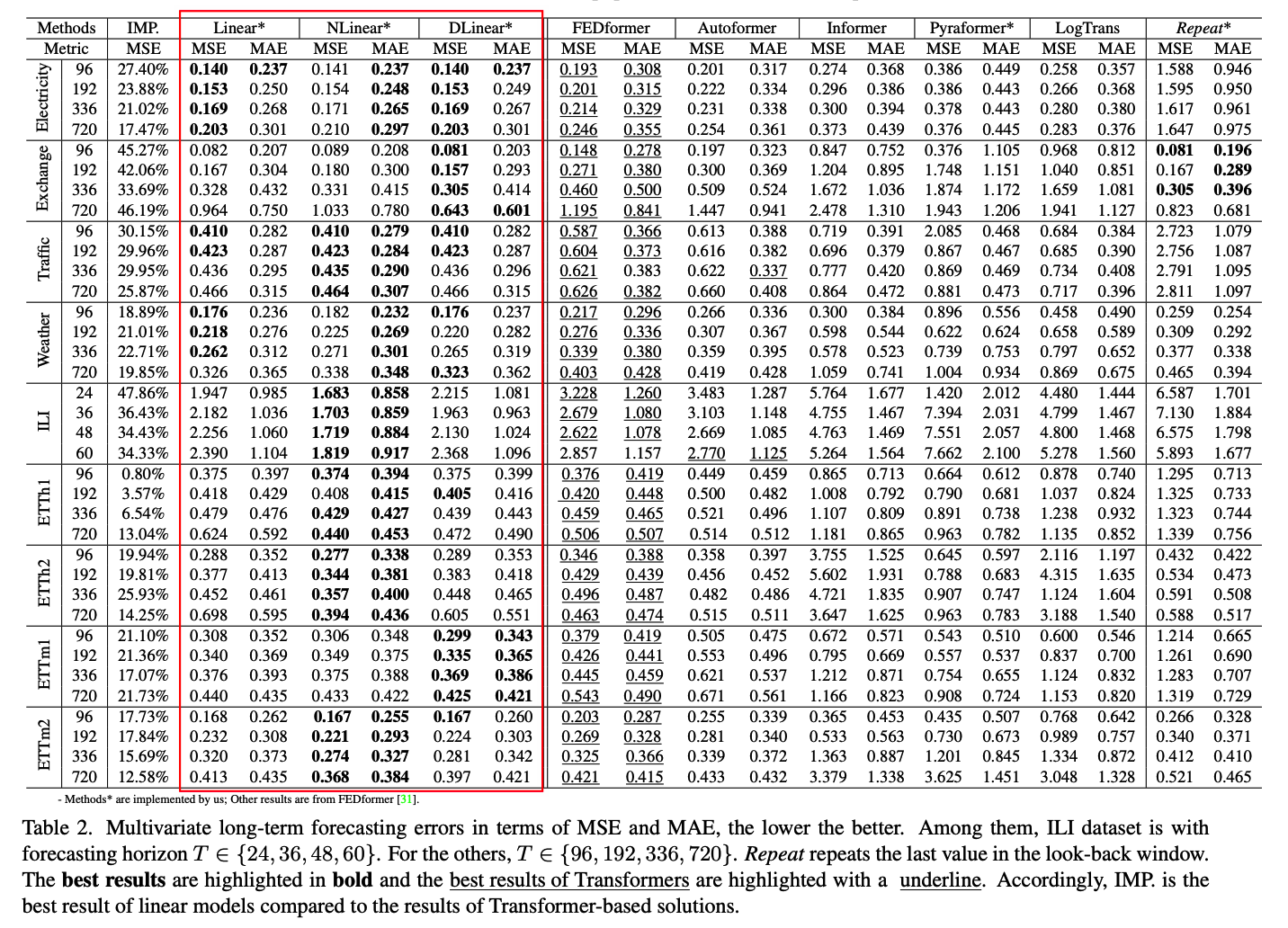
(2) Comparison with Transformers
a) Quantitative results
MTS forecasting
( note: LTSFLinear even does not model correlations among variates )
UTS forecasting (appendix)
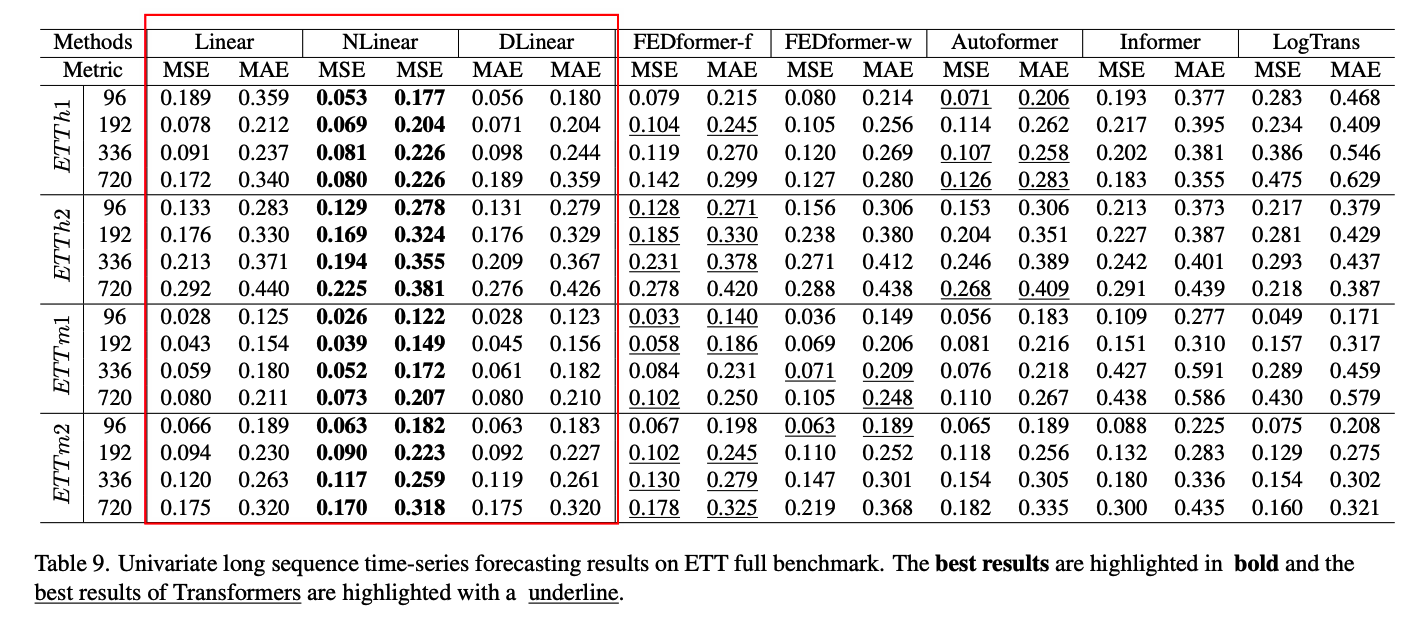
FEDformer
- achieves competitive forecasting accuracy on ETTh1.
- reason) FEDformer employs classical time series analysis techniques such as frequency processing
- which brings in TS inductive bias & benefits the ability of temporal feature extraction.
Summary
-
(1) existing complex Transformer-based LTSF solutions are not seemingly effective
-
(2) surprising result : naive Repeat outperforms all Transformer-based methods on Exchange-Rate
\(\rightarrow\) due to wrong prediction of trends in Transformer-based solutions
- overfit toward sudden change noises in the training data
b) Qualitative results
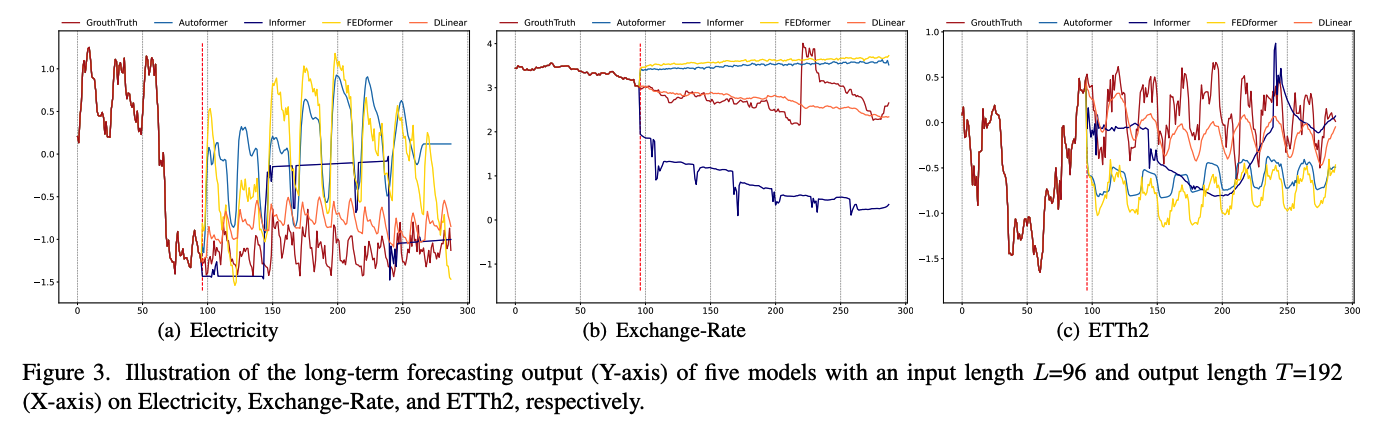
the prediction results on 3 TS datasets
- input length \(L\) = 96
- output length \(T\) = 336
[ Electricity and ETTh2 ] Transformers fail to capture the scale and bias of the future data
[ Exchange-Rate ] hardly predict a proper trend on aperiodic data
(3) More Analyses on LTSF-Transformers
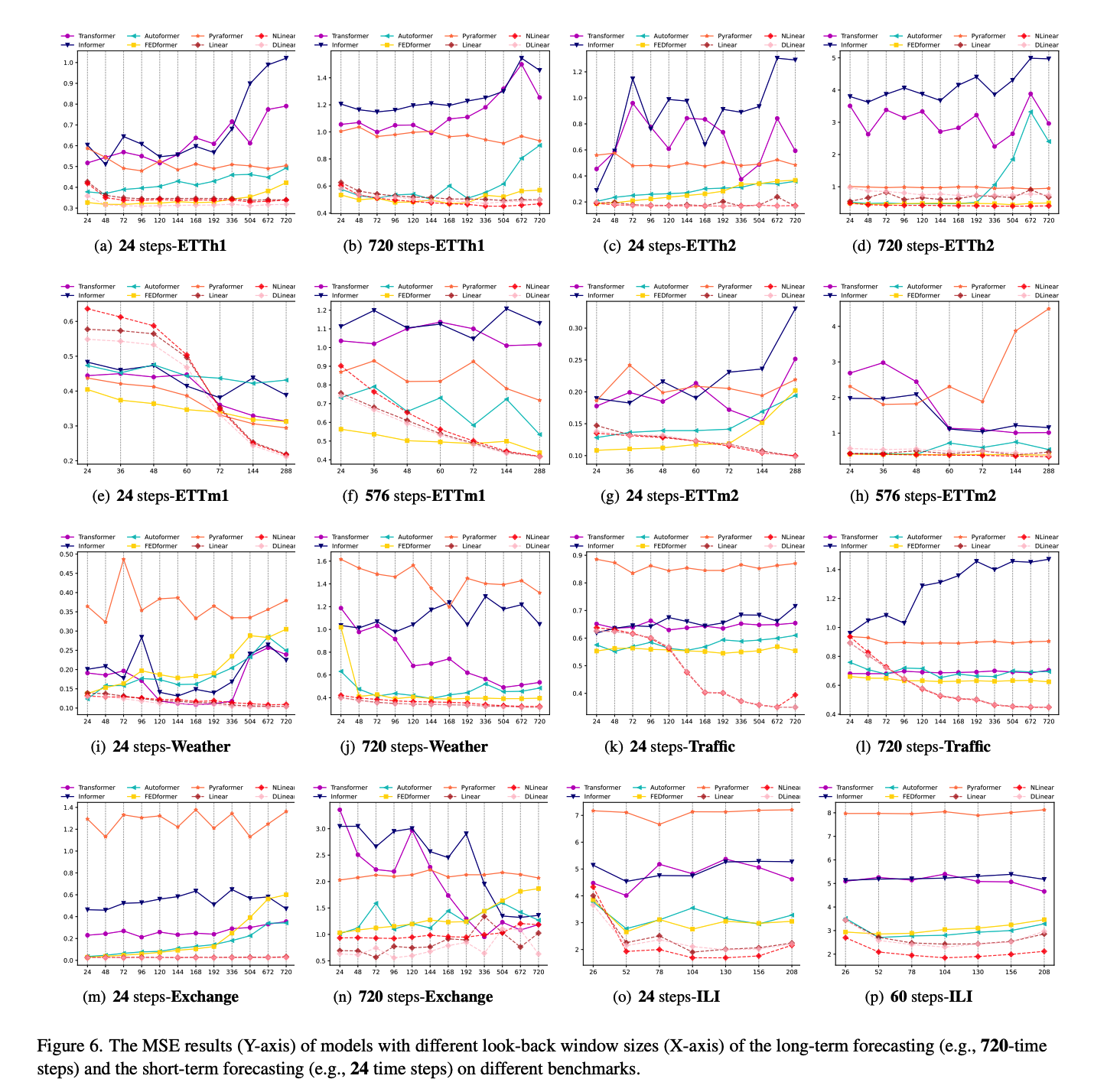
Q1. Can existing LTSF-Transformers extract temporal relations well from longer input sequences?
Size of the look-back window \(L\)
- greatly impacts forecasting accuracy
Powerful TSF model with a strong temporal relation extraction capability :
- larger \(L\), better results!
To study the impact of \(L\)…
- conduct experiments with \(L \in\) \(\{24,48,72,96,120,144,168,192,336,504,672,720\}\)
- where \(T\) = 720
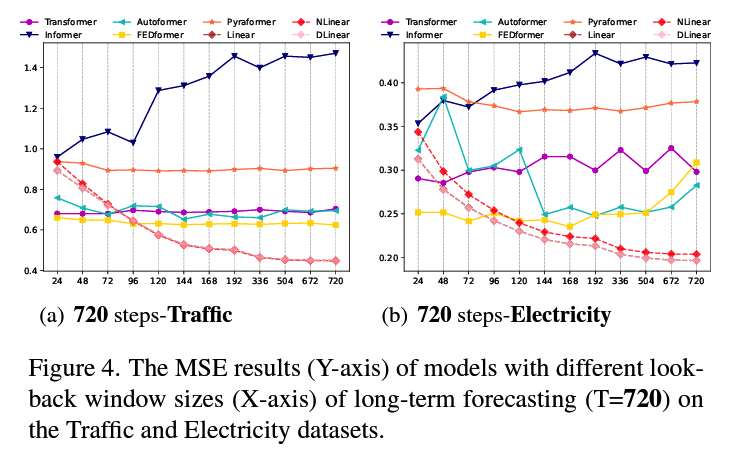
- existing Transformer-based models’ performance deteriorates or stays stable, when larger \(L\)
- ( \(\leftrightarrow\) LTSF-Linear : boosted with larger \(L\) )
\(\rightarrow\) Transformers : tend to overfit temporal noises
( thus input size 96 is exactly suitable for most Transformers )
Q2. What can be learned for long-term forecasting?
Hypothesize that long-term forecasting depends on whether models can capture the trend and periodicity well only.
( That is, the farther the forecasting horizon, the less impact the look-back window itself has. )
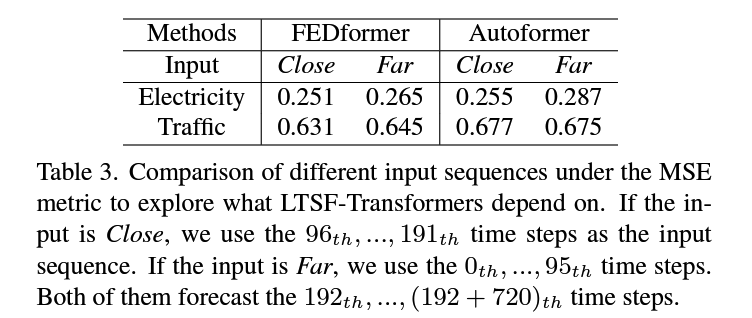
Experiment
- \(T\) = 720 time steps
- Lookback \(L\) = 96
- ver 1) original input \(\mathrm{L}=96\) setting (called Close)
- ver 2) far input \(\mathrm{L}=96\) setting (called Far)
…
6. Implementation Details
For existing Transformer-based TSF solutions:
- Autoformer, Informer, and the vanilla Transformer : from Autoformer [28]
- FEDformer and Pyraformer : from their respective code
( + adopt their default hyper-parameters to train the models )
DLinear
- MA kernel size fo 25 ( same as Autoformer )
- # of params
- Linear : \(T\times L\)
- NLinear : \(T\times L\)
- DLinear : \(2\times T\times L\)
- LTSF-Linear will be underfitting when the \(L\) is small
- LTSF-Transformers tend to overfit when \(L\) is large
To compare the best performance of existing LTSF-Transformers with LTSF-Linear
- use \(L=336\) for LTSF-Linear
- use \(L=96\) for Transformers
7. LTSF & STSF
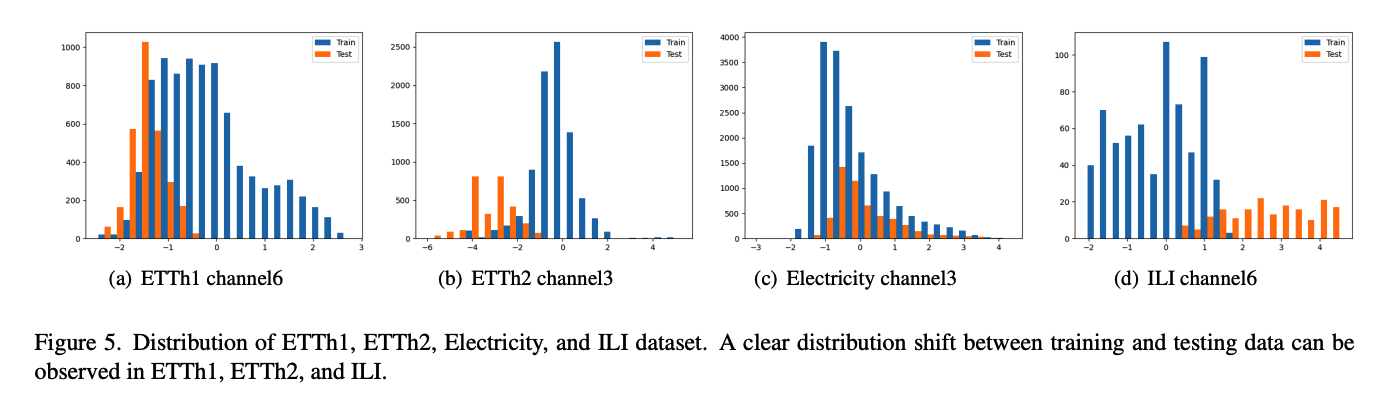
8. Distribution shift
Train vs Test