ModernTCN; A Modern Pure Convolution Structure for General TS Analysis

ModernTCN: A Modern Pure Convolution Structure for General TS Analysis

Contents

1. Abstract
2. Introduction
3. Related Works
   1. CNN in TS
   2. CNN in CV
4. Modern TCN
   1. Modernize 1D CNN
   2. TS related modification
   3. Overall structure
5. Experiments

Abstract

Time Series: convolution is losing steam !

\(\rightarrow\) This paper modernize the traditional TCN = ModernTCN

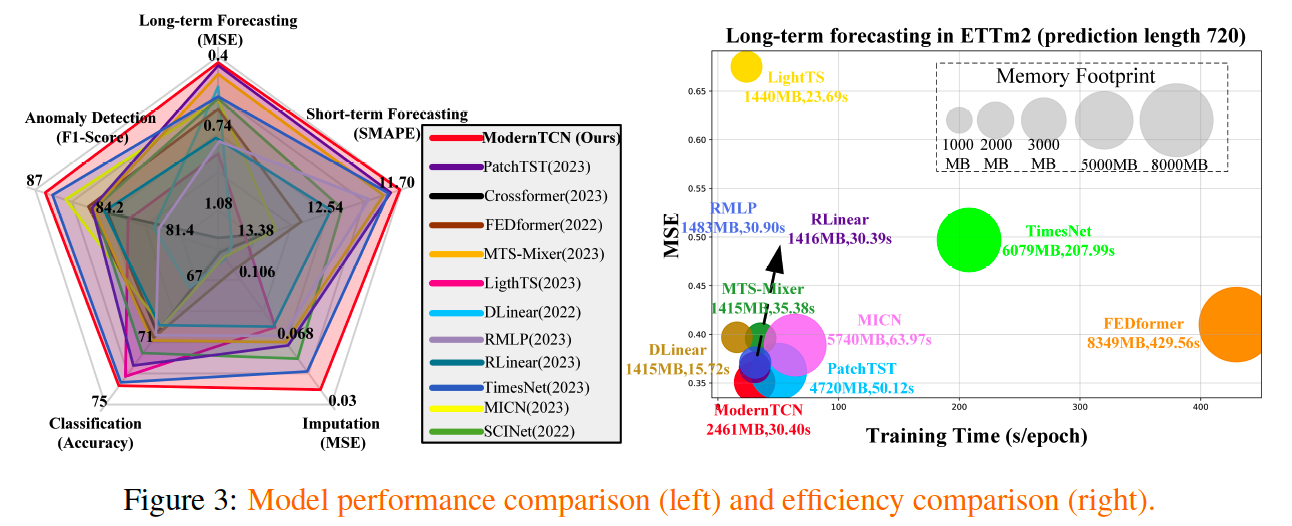
• SOTA in 5 TS tasks

1. Introduction

TS domain

Previous CNN based models (Wang et al., 2023; Liu et al., 2022a)

• Bring CNN back to TS

• However, mainly focus on designing extra sophisticated structures

  \(\rightarrow\) ignoring the importance of updating the convolution!

• Inferior to Transformer/MLP ( reason: Figure 1 )

\(\rightarrow\) Increasing the ERF is the key!!

Q) How to beetter use CNN in TS?

Vision domain

Different path to explore CNN

Latest vision CNN

• Focus on optmizing the CNN itself & prorpose modern convolution
• Modern convolution
  • incorporate some architectural designs in Transformer ( FIgure 2-b )
  • adopt large kernel

\(\rightarrow\) but still not discussed in TS domain

Potential of CNN

• Efficient way to capture cross-variable dependency

  ( = among variables in MTS )

• previous works have used to capture it…but not competitive….

\(\rightarrow\) Thus need some modification!

ModernTCN

• Propose a modern pure convolution structure

• Efficiently utilize

  • cross-time
  • cross-variable

  dependency for TS task

• 5 TS tasks

2. Related Works

(1) CNN in TS

• MICN (Wang et al., 2023)
• SCINet (Liu et al., 2022)
• TimesNet (Wu et al., 2023)

(2) CNN in CV

CNN

• used to be the dominant backbone ( before ViTs )

ConvNext (Liu et al., 2022)

• redesign CNN to make it similar to Transformer

RepLKNet (Ding et al., 2022)

• scales the kernel size to 31x31
• with the help of Structural Reparameter technique

SLaK (Liu et al., 2022)

• scales the kernel size to 51x51
• by decomposing a large kernel into 2 rectangular parallel kernels & dynamic sparsity

This paper: modernize & modify 1D CNN in TS

3. ModernTCN

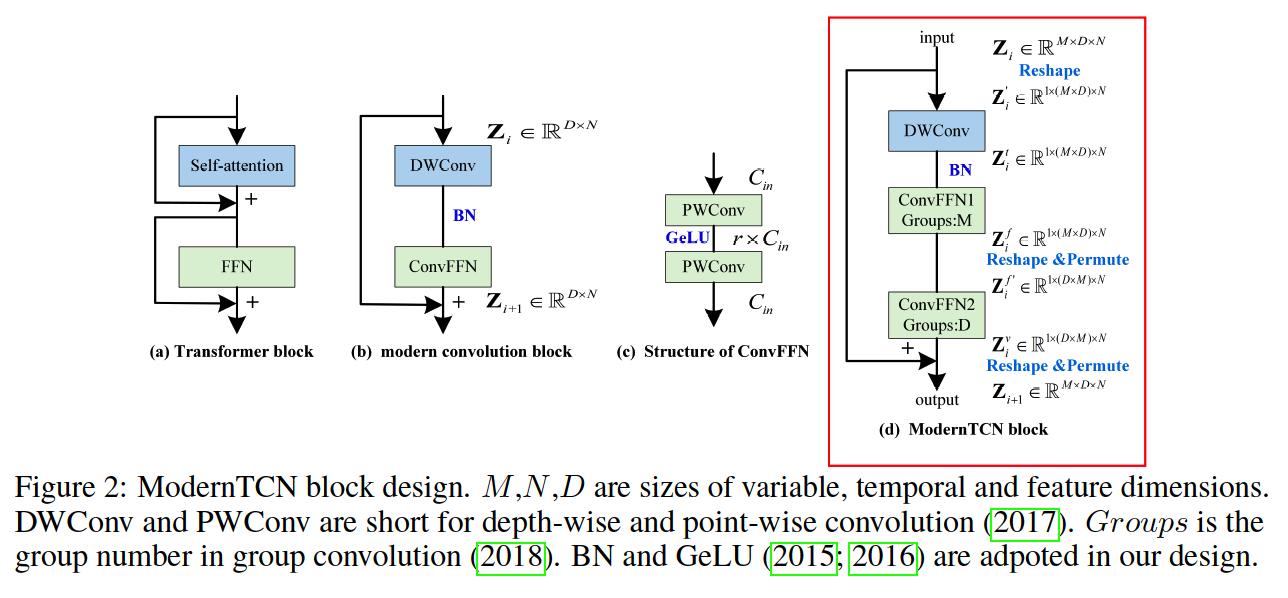
(1) Modernize 1D CNN

Re-design the 1D CNN

• (1) DWConv ( DW = Depth-Wise )
• (2) ConvFFN ( FFN = Feed-Forward NN )

a) DWConv

( = self-attention in Transformer )

• learn the temporal info among tokens on a PER-FEATURE basis

b) ConvFFN

( = FFN in Transformer )

• consists of 2 PWConvs
• PWConvs ( PW = Point-Wise )
  • adopts an inverted bottle neck structure
  • hidden channel of ConvFFN = \(r \times\) channel of input
• learn new feature representation of each token INDEPENDENTLY

\(\rightarrow\) Above design leads to a separation of temporal and feature information mixing

Traditional CNN vs. Modern TCN

• Traditional) jointly mix TEMPORAL & FEATURE
• Modern) separate TEMPORAL & FEATURE

Compared to CV… TS also has VARIABLE dimension

\(\rightarrow\) cross-variable info is also critical in MTS

\(\rightarrow\) more modifications are needed for TS

(2) TS related modification

a) Maintaining the Variable Dimension

Embedding layer in CV

• Before the backbone, we embed 3 channel RGB features at each pixel into a \(D\)-dim vector
• However, such variable-mixing embedding is not suitable for TS
  • Reason 1) Diifference among variables in TS
    • much greater than difference among RGB channels
  • Reason 20 Leads to the discard of variable dimension
    • making it unable to further study the cross-variable dependency

\(\rightarrow\) Propose patchify variable-independent embedding

Notation

• \(\mathbf{X}_{i n} \in \mathbb{R}^{M \times L}\) : TS of \(M\) variables of length \(L\)
  • divide it into \(N\) patches of patch size \(P\) after proper padding
  • stride = \(S\) = length of non overlapping region
• \(\mathbf{X}_{e m b}=\operatorname{Embedding}\left(\mathbf{X}_{i n}\right) \in \mathbb{R}^{M \times D \times N}\).

\(\mathbf{X}_{e m b}=\operatorname{Embedding}\left(\mathbf{X}_{i n}\right)\)

• Different from previous studies (Nie et al., 2023; Zhang \& Yan, 2023), we conduct this patchify embedding in an equivalent fully-convolution way for a simpler implementation.

• Step 1) Unsqueezing the shape to \(\mathbf{X}_{i n} \in \mathbb{R}^{M \times 1 \times L}\)

• Step 2) Feed the padded \(\mathbf{X}_{i n}\) into a 1D CNN stem layer

  • Stem layer = kernel size \(P\) & stride \(S\).
  • Maps 1 input channel into \(D\) output channels.
  • Each of the \(M\) univariate TS is embedded independently

  \(\rightarrow\) able to keep the variable dimension

Followings are modifications to make our structure able to capture information from the additional variable dimension.

b) DWConv

Originally designed for learning the temporal information

Difficult to jointly learn both CROSS-TIME & CROSS-VARIABLE dependency

Thus, modify the original DWConv …

• from ) feature independent
• to ) feature and variable independent

\(\rightarrow\) treat each UTS independently

Also, adopt large kernel to increase ERFs

c) ConvFFN

( DWConv: feature & variable independent )

\(\rightarrow\) ConvFFN should MIX the information across feature & variable dimension

• naive way) jointly learn

  \(\rightarrow\) however, lead to higher complexity & worse performance

• solution) DECOUPLE it!

  • (1) ConvFFN1: for feature representation per variable
  • (2) ConvFFN2: for cross-variable dependency per feature

(3) Overall Structure

\(\mathbf{X}_{e m b}=\operatorname{Embedding}\left(\mathbf{X}_{i n}\right)\).

\(\mathbf{Z}=\operatorname{Backbone}\left(\mathbf{X}_{e m b}\right)\).

\(\mathbf{Z}_{i+1}=\operatorname{Block}\left(\mathbf{Z}_i\right)+\mathbf{Z}_i\).

4. Experiments

Baselines

Transformer-based models:

• PatchTST (2023), Crossformer (2023) and FEDformer (2022)

MLP-based models:

• MTS-Mixer (2023b), LightTS (2022), DLinear (2022), RLinear and RMLP (2023a)

Convolution-based Model:

• TimesNet (2023), MICN (2023) and SCINet (2022a).

Results