iTransformer; Inverted Transformers are Effective for Time Series Forecasting

iTransformer: Inverted Transformers are Effective for Time Series Forecasting

Contents

1. Abstract
2. Introduction
3. iTransformer
4. Experiments

Abstract

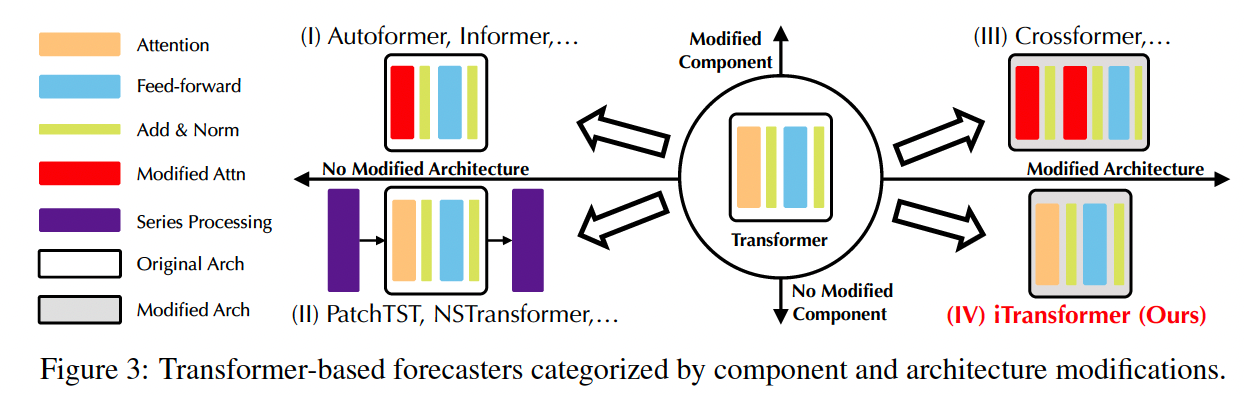
Linear forecasting models vs. Transformer-based forecasters

This paper:

• Reflect on the competent duties of Transformer components
• Repurpose the Transformer architecture
  • without any modification to the basic components
• Propose iTransformer

iTransformer

• Simply applies the attention and feed-forward network on the inverted dimensions
• Time points of individual series are embedded into variate tokens
  • utilized by the attention mechanism to capture multivariate correlations
• Feed-forward network: applied for each variate token to learn nonlinear representations

1. Introduction

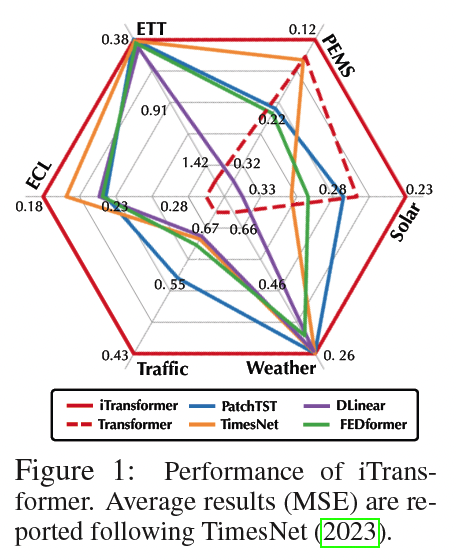
Question the validity of Transformer-based forecasters

• (Before)

  • (1) Embed multiple variates of the same timestamp into indistinguishable channels
  • (2) Apply attention on these temporal tokens to capture temporal dependencies

• Considering the numerical but less semantic relationship among time points,

  researchers find that simple linear layers outperform them!!

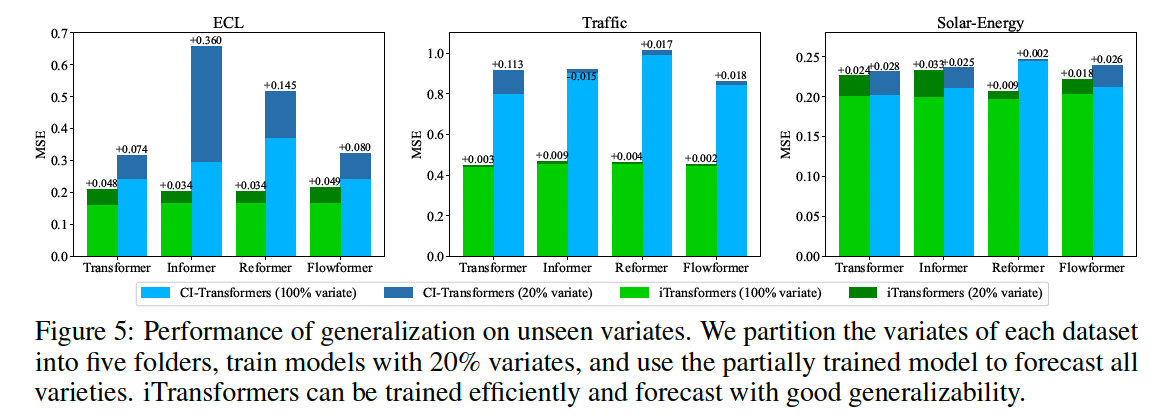
Meanwhile, ensuring Channel Indepenence (CI) & utilizing mutual information is ever more highlighted by recent research

\(\rightarrow\) Can be hardly achieved without subverting the vanilla Transformer architecture.

This paper: Reflect on why Transformers perform even worse than linear models in TS forecasting

( while acting predominantly in many other fields )

• May be not suitable for MTS forecasting.

(Figure 2 - Top)

• Points of the same time step ( that basically represent completely different physical meanings recorded by inconsistent measurements ) are embedded into one token with wiped-out multivariate correlations.
• Token formed by a single time step can struggle to reveal beneficial information
  • due to excessively local receptive field & time-unaligned events represented by simultaneous time points.
• Besides, while series variations can be greatly influenced by the sequence order, permutation invariant attention mechanisms are improperly adopted on the temporal dimension

\(\rightarrow\) Transformer is weakened to capture essential series representations and portray multivariate correlations

iTransformer

Key Point = Inverted view on TS

• Inverting = Embedding the whole TS of each variate independently into a (variate) token

  ( = extreme case of Patching that enlarges local receptive field )

• By inverting, the embedded token aggregates the global representations of series that can be more variate-centric and better leveraged by booming attention mechanisms for multivariate correlating
• Feed-forward network: can be proficient enough to learn generalizable representations for distinct variates encoded from arbitrary lookback series and decoded to predict future series.

Summary

It is not that Transformer is ineffective for TS forecasting!

Rather it is improperly used!

Advocate iTransformer as a fundamental backbone for TS forecasting

• Step 1) Embed each TS as variate tokens
• Step 2) Adopt the attention for multivariate correlations
• Step 3) Employ the feed-forward network for TS representations

2. iTransformer

Notation

• Input: \(\mathbf{X}=\left\{\mathbf{x}_1, \ldots, \mathbf{x}_T\right\} \in \mathbb{R}^{T \times N}\)
• Target: \(\mathbf{Y}=\left\{\mathbf{x}_{T+1}, \ldots, \mathbf{x}_{T+S}\right\} \in\) \(\mathbb{R}^{S \times N}\).

Note that..

• \(\mathbf{X}_{t,:}\) : May not contain time points that essentially reflect the same event
  • \(\because\) Systematical time lags among variatesin the dataset
• Elements of \(\mathbf{X}_{t, \text { : }}\) : Can be distinct from each other, for which a variate \(\mathbf{X}_{:, n}\) generally shares.

(1) Structure Overview

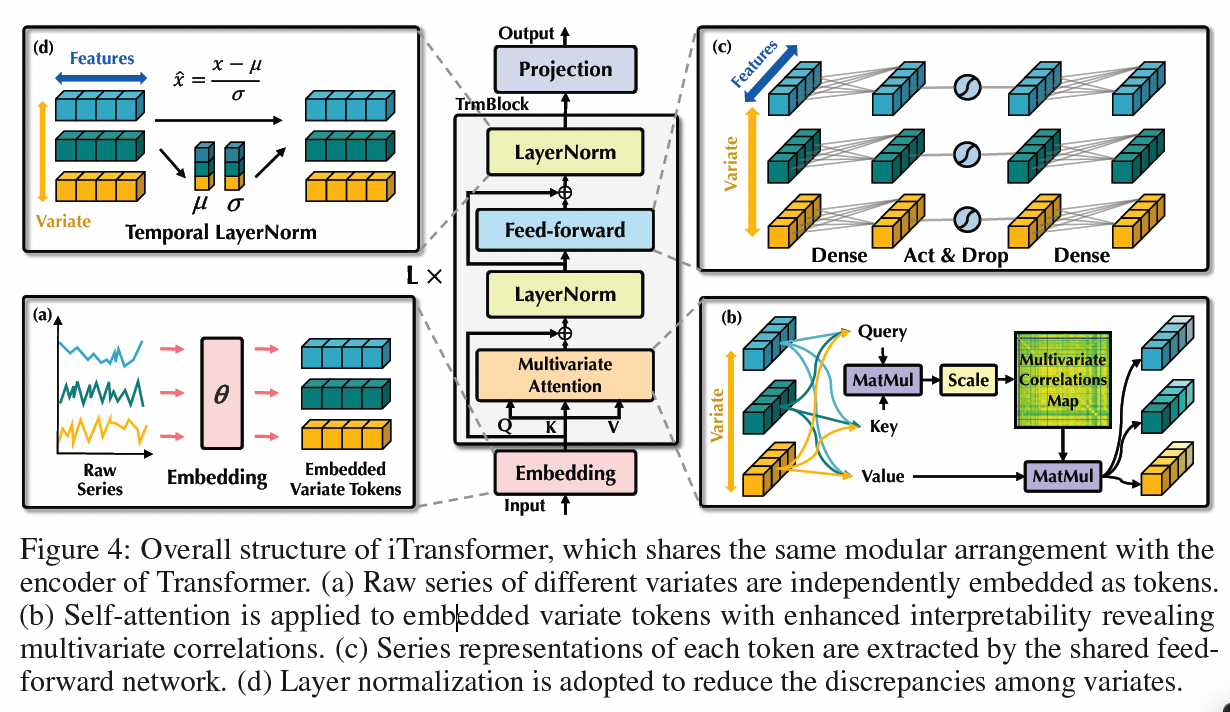
• Encoder-only architecture of Transformer
  • including the embedding, projection, and Transformer blocks.

a) Embedding the whole series as the token

(Most Transformer)

• Regard multiple variates of the same time as the (temporal) token

(iTransformer)

• Find that the above approach on the numerical modality can be less instructive for learning attention maps

• Focuses on representation learning and adaptive correlating of multivariate series

Procedure

• Step 1) Each TS is tokenized to describe the properties of the variate

• Step 2) Apply self-attention for mutual interactions
• Step 3) Individually processed by feed-forward networks for TS representations

\(\begin{aligned} \mathbf{h}_n^0 & =\operatorname{Embedding}\left(\mathbf{X}_{:, n}\right), \\ \mathbf{H}^{l+1} & =\operatorname{TrmBlock}\left(\mathbf{H}^l\right), l=0, \cdots, L-1, \\ \hat{\mathbf{Y}}_{:, n} & =\operatorname{Projection}\left(\mathbf{h}_n^L\right), \end{aligned}\).

b) iTransformers

• No more specific requirements on Transformer variants
  • other than the attention is applicable for multivariate correlation
• Bundle of efficient attention mechanisms can be the plugins

(2) Inverted Transformer Components

pass

3. Experiments