(paper) Adversarial Sparse Transformer for Time Series Forecasting

Adversarial Sparse Transformer for Time Series Forecasting (2020)

Contents

1. Abstract
2. Introduction
3. Background
   1. Problem Definition
   2. Transformer
   3. GAN
4. Model
   1. Sparse Transformer
   2. Adversarial Training

0. Abstract

Time Series Forecasting의 2가지 문제점

• 1) 대부분 “point prediction”

  \(\rightarrow\) hardly capture stochasticity of data

• 2) inference 단계에서의 error accumulation

  \(\rightarrow\) 주로 auto-regressive generative mode 사용함

  • (train 중) ground-truth가 다음 input으로
  • (inference 중) 앞 step의 예측값이 다음 input으로

Propose a new time series forecasting model : “AST”

AST ( Adversarial Sparse Transformer ) based on GANs

• (generator로써) Sparse Transformer
  • learn a sparse attention map for TS forecast
• (discriminator) improve prediction performance

1. Introduction

Modeling Sequential data with DNN

최근 들어, DNN 사용하여 sequential data 다룸

• 문제점 1) 대부분 하나의 objective function만을 사용 ( likelihood loss, MSE loss, … )
  • 현실의 dataset은 stochasticity를 가져서, specific non-flexible objective만으로는..
• 문제점 2) error accumulation
  • abstract에서 소개

Adversarial Sparse Transformer

AST = (1) + (2)

• (1) modified Transformer
• (2) GANs

discriminator can “regularize” the modified transformer at sequence level

& make it learn a better representation \(\rightarrow\) eliminate error accumulation

Contribution

• 1) effective time series forecasting model (AST)를 제안함
• 2) design Generative Adversarial Encoder-Decoder framework to regularize the model

2. Background

(1) Problem Definition

• Interval Prediction은 여러 곳에서 유용하다

  ex) Quantile Regression

• 이 모델에서는 quantile regression을 수행한다

  ( outputting 50th, 90th percentile at each time step )

Notation

• \(\left\{\mathbf{y}_{i, 1: t_{0}}\right\}_{i=1}^{S}\) : \(S\)개의 univariate time series
  • \(\mathbf{y}_{i, 1: t_{0}}=\) \(S\)개 중 \(i\) 번째 time series
• \(\mathbf{X}_{i, 1: t_{0}} \in \mathbb{R}^{t_{0} \times k}\) : \(k\) 차원의 time-independent / time-dependent 변수 ( = covariates )

목적 : predict the values of the next \(\tau\) time steps of each quantile for all time series given the past

• \(\hat{\mathbf{Y}}_{\rho, t_{0}+1: t_{0}+\tau}=f_{\rho}\left(\mathbf{Y}_{1: t_{0}}, \mathbf{X}_{1: t_{0}+\tau} ; \Phi\right)\).
  • \(\hat{\mathbf{Y}}_{\rho, t}\) : \(\rho^{t h}\) quantile prediction value in the \(t\) time step
  • \(f_{\rho}\) : prediction model for \(\rho^{t h}\) quantile
  • \(\Phi \in \mathbb{R}\) : learnable parameters of the model
• \(\left\{\mathbf{Y}_{1: t_{0}}\right\}\) : target time series
• \(\left[1, t_{0}\right]\) : conditioning range
• \(\left[t_{0}+1, t_{0}+\tau\right]\) : prediction range
  • \(t_{0}+1\) : forecast start time
  • \(\tau \in \mathbb{N}\) : forecast horizon
• our model output forecasts of different quantiles by the corresponding quantile objectives.

(2) Transformer

output of \(m\) -th head \(\mathbf{O}_{m}\) :

• \(\mathbf{O}_{m}=\alpha_{m} \mathbf{V}_{m}=\operatorname{softmax}\left(\frac{\mathbf{Q}_{m} \mathbf{K}_{m}^{T}}{\sqrt{d_{k}}}\right) \mathbf{V}_{m}\).

The output of the multi-head attention layer :

• linear projection of the concatenation of \(\mathrm{O}_{1}, \mathrm{O}_{2}, \ldots, \mathrm{O}_{m} .\)

• \(F F N(\mathbf{O})=\max \left(0, \mathbf{O W}_{1}+\mathbf{b}_{1}\right) \mathbf{W}_{2}+\mathbf{b}_{2}\).

(3) GAN

생략

3. Model

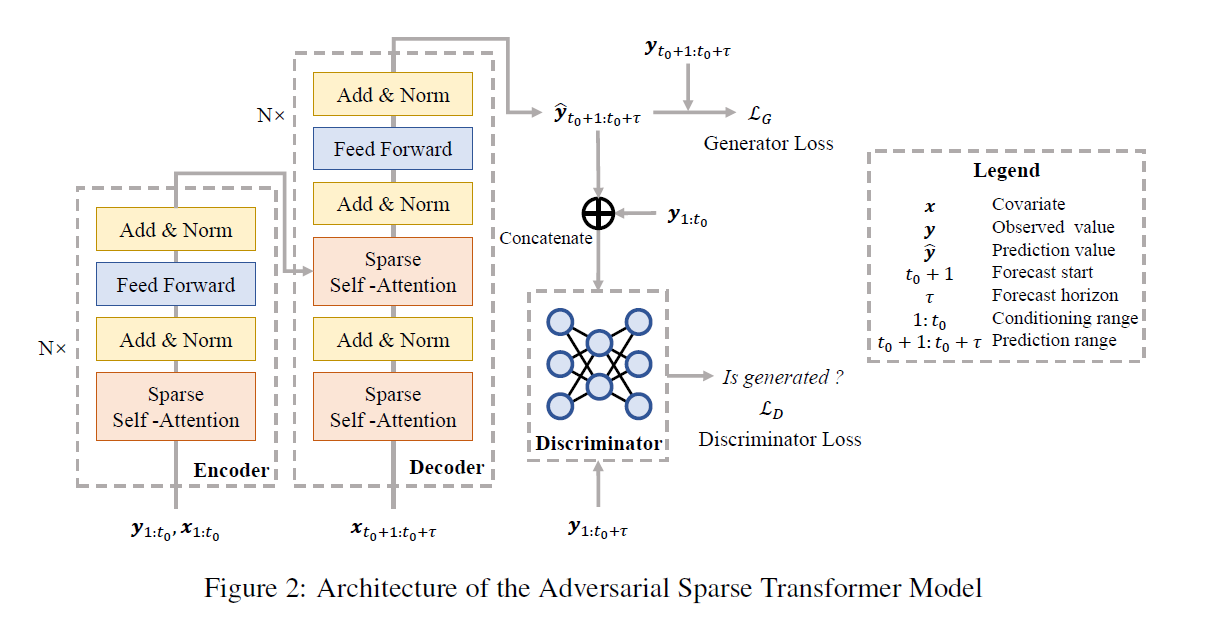
Our model is based on “encoder-decoder” + “auxiliary discriminator”

• Encoder의 input : \(\left[\mathbf{Y}_{1: t_{0}}, \mathbf{X}_{1: t_{0}}\right]\)
• Encoder의 output : \(\left(\mathbf{h}_{1}, \ldots, \mathbf{h}_{t_{0}}\right)\)
• Decoder의 input : Encoder의 output & \(\mathrm{X}_{t_{0}: t_{0}+\tau}\)
• Decoder의 output : prediction

(1) Sparse Transformer

핵심 : “should pay no attention to those irrelevant steps”

\(\rightarrow\) learning networks with sparse mappings!

이 논문에서는, focus on a more recent and flexible family of transformations, \(\alpha\) -entmax

• \(\alpha-\operatorname{entmax}(\mathbf{h})=[(\alpha-1) \mathbf{h}-\tau \mathbf{1}]_{+}^{1 / \alpha-1}\).

  • \([\cdot]_{+}\) : ReLU
  • \(\mathbf{1}\) : one-vector
  • \(\tau\) : Lagrange multiplier

• Simply replace softmax with \(\alpha\) -entmax in the attention heads,

  \(\rightarrow\) lead to sparse attention weights!

• \(\alpha=1\) : softmax function

• \(\alpha=2\) : sparse mapping

• 이 논문에서는 \(\alpha=1.5\)로 setting

(2) Adversarial Training

대부분의 모델들은 optimize “specific objective function”

• 이러한 loss function은 real-world stochasticity in time series를 잘 못잡아내

\(\rightarrow\) 이러한 문제를 완화하기 위해, propose an adversarial training process

• to regularize the encoder-decoder
• to improve the accuracy at the sequence level