(paper) Clustering Time Series Data through Autoencoder-based Deep Learning Models

Clustering Time Series Data through Autoencoder-based Deep Learning Models (2020)

Contents

1. Abstract
2. Introduction
3. Literature Review
   1. t.s. Representation methods
   2. t.s. Similarity/Distance Measures methods
   3. t.s. Cluster Prototypes
   4. t.s. Clustering Algorithm
4. Feature Vectors of Time Series as Data Labels
   1. Common general components of t.s data
5. A Synergic method for t.s Clustering
   1. Stage 1 : Label Generation
   2. Stage 2 : Autoencoder-based Clustering

0. Abstract

Clustering = optimization problem & iterative process

goal :

• MAXIMIZE the similarities of data items &
• MINIMIZE the similarities of data objects grouped in separate clusters

heavily depends on dimension ( = number of features to be considered )

\(\rightarrow\) identification of hidden features!

This paper introduces…. TWO-stage method for clustering TIME-SERIES data

• step 1) utilize the characteristic of given time series data

  \(\rightarrow\) create LABELS ( make it as SUPERVISED learning )

• step 2) autoencoder-based DL

  • learn & model both the known/hidden features of t.s.data

1. Introduction

Challenges with TSC (Time Series Clustering)

• 1) Unlabeled data
• 2) High dimensionality
• 3) Hidden features

Contributions

• 1) two-stage methodology ( introduction 참고하기 )
• 2) case study performed on clustering time series data of 70 stock indices

2. Literature Review

TS clustering = 3 main categories

• [1] Whole time-series clustering

  • cluster a set of individual time-series

• [2] Subsequence clustering

  • only performed on a single time-series

  • single time-series is divided into multiple segments

• [3] Time Point clustering

  • only performed on a single time-series

  • not required to assign all points to clusters

    ( = some can be noise )

This paper reviews only [1] Whole time-series clustering

Whole time-series clustering = 3 different approaches

• 1) shape-based
• 2) feature-based
• 3) model-based

Whole time-series clustering = 2 categories

( w.r.t the length of time series )

• a) shape-level
• b) structure-level

a) shape-based approach

• based on shape similarity
• matched using a non-linear stretching
• conventional clustering methods

b) feature-based approach

• key : feature extraction

• (1) transform the raw time-series into the set of features

  ( + dimensionality reduction )

• (2) then, use conventional clustering algorithm in lower dimension

c) model-based approach

• assume a model for each cluster

  ( & fit the data into the assumed model )

• each raw t.s data is transformed into either..

  • 1) model parameters ( = one model for each t.s )
  • 2) mixture of underlying probability distn

Whole time-series clustering’s 4 major components

• 1) dimensionality reduction
• 2) distance measurement ( similarity )
• 3) clustering algorithm
• 4) prototype definition & evaluation

(1) t.s. Representation methods

dimensionality reduction

• 1) reduces memory requirements
• 2) speeds up

4 types of t.s representation methods

• 1) data adaptive :
  • minimize the global reconstruction error
• 2) non-data adaptive
  • only appropriate for t.s with FIXED-size
• 3) model-based
  • represent t.s in a stochastic way
  • ex) HMM, statistical models, ARMA
• 4) data-dictated ( clipped data )
  • feature reduction ratio is automatically defined according on raw time-series
  • ex) clipping (bit-level) representation

(2) t.s. Similarity/Distance Measures methods

2 categories of similarity/distance measure approaches

• 1) clustering according to objectives

  • similarity in time/shape/change

  • (time)

    • similar t.s are discovered on each time step
    • calculated using RAW t.s …… expensive

  • (shape)

    • similar shape, regardless of time points

      ( similar trends, at different time : OK )

    • ex) DTW (Dynamic Time Warping)

  • (change)

    • = structural similarity
    • 1) t.s data is first modeled using modeling methods ( ex. HMM, ARMA…)
    • 2) then similarity metric is measured, based on global feature extracted
    • appropriate for long time-series

• 2) clustering according to the length of time-series

  • shape level : for short-length
  • structure level : for long-length

(3) t.s. Cluster Prototypes

3 main methods to obtain cluster prototypes

• 1) Medoid prototype

  • defined as member of cluster,

    such that its dissimilarities to all other members in the cluster is minimum

• 2) Averaging prototype

  • mean of time-series at each point
  • used when time-series have equal length ( DTW (X) )

• 3) Local Search prototype

  • step 1) medoid of cluster is computed
  • step 2) warping paths techniques are used to calculate average prototype

(4) t.s. Clustering Algorithm

• 1) hierarchical
• 2) partitioning-based
• 3) density-based
• 4) grid-based
• 5) model-based
• 6) multi-step based ( = hybrid )

3. Feature Vectors of Time Series as Data Labels

(1) Common general components of t.s data

• 1) seasonality
• 2) cycle
• 3) trend
• 4) irregular features

4. A Synergic method for t.s Clustering

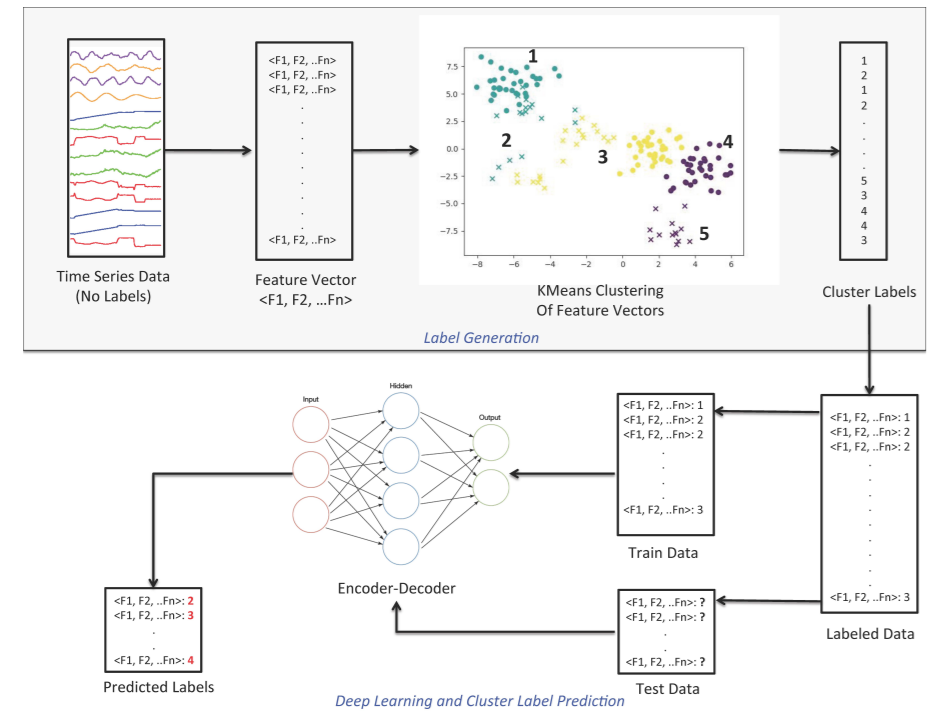
(1) Stage 1 : Label Generation

(2) Stage 2 : Autoencoder-based Clustering