Probabilistic Forecasting with Temporal Convolutional Neural Network (2020)
Contents
- Abstract
- Introduction
- Classical forecasting methods
- DL based methods
- Dilated causal convolutional architectures
- Auto vs Non-Autoregressive
- (proposal) DeepTCN
- Method
- NN architecture
- Encoder : Dilated Causal Convolutions
- Decoder : Residual Neural Network
- Probabilistic forecasting framework
- Input Features
0. Abstract
probabilistic forecasting, baed on CNN
- under both 1) parametric and 2) non-parametric settings
- stacked residual blocks, based on dilated causal convolutional nets
- able to learn complex patterns, such as seasonality, holiday effects
1. Introduction
instead of predicting individual/small number of t.s…
\(\rightarrow\) needs to predict thousands/millions of related t.s
1) Classical forecasting methods
- ARIMA (Autoregressive Integrated Moving Average)
- exponential smoothing ( for univariate base-level forecasting )
- ARIMAX = ARIMA + eXogeneous variable
\(\rightarrow\) however, working with thousands/millions of series requires prohibitive labor and computing resources for parameter estimation & not applicable when historical data is sparse / unavailable
2) DL based methods
- RNN
- Seq2Seq
- GRU
\(\rightarrow\) BPTT hampers efficient computations
3) Dilated causal convolutional architectures
-
Wavenet : alternative for modeling sequential data
-
staking layers of DCC … receptive fields can be increased
( w.o violating temporal orders )
-
can be performed in parallel
4) Auto vs Non-Autoregressive
Autoregressive models
- ex) seq2seq, wavenet
- factorize the joint distn
- one-step-ahead prediction approach
Non-Autoregressive models
- direct prediction strategy
- usually better performances
- avoid error accumulation
- can be parallelized
5) (proposal) DeepTCN
Deep Temporal Convolutional Network
-
non-autoregressive probabilistic forecasting
-
Contributions
- 1) CNN-based forecasting framework
- 2) high scalability & extensibility
- 3) very flexible & include exogenous covariates
- 4) both point & probabilistic forecasting
2. Method
Notation
- \(\mathbf{y}_{1: t}=\left\{y_{1: t}^{(i)}\right\}_{i=1}^{N}\) : set of time series ( Multivariate…number of time series \(N\) )
- \(\mathbf{y}_{(t+1):(t+\Omega)}=\left\{y_{(t+1):(t+\Omega)}^{(i)}\right\}_{i=1}^{N}\) : future time series
- \(t\) : length of historical observations
- \(\Omega\) : length of forecasting horizon
- goal : model the conditional distribution of the future time series \(P\left(\mathbf{y}_{(t+1):(t+\Omega)} \mid \mathbf{y}_{1: t}\right)\)
1) Classical generative models
- factorize the joint probability
- \(P\left(\mathbf{y}_{(t+1):(t+\Omega)} \mid \mathbf{y}_{1: t}\right)=\prod_{\omega=1}^{\Omega} p\left(\mathbf{y}_{t+\omega} \mid \mathbf{y}_{1: t+\omega-1}\right)\).
- challenges
- 1) efficiency issue
- 2) error accumulation
2) Our framework
- joint distn DIRECTLY
- \(P\left(\mathbf{y}_{(t+1):(t+\Omega)} \mid \mathbf{y}_{1: t}\right)=\prod_{\omega=1}^{\Omega} p\left(\mathbf{y}_{t+\omega} \mid \mathbf{y}_{1: t}\right)\).
- important to allows covariates \(X_{t+\omega}^{(i)}\) (where \(\omega=1, \ldots, \Omega\) and \(\left.i=1, \ldots, N\right)\) t
- \(P\left(\mathbf{y}_{(t+1):(t+\Omega)} \mid \mathbf{y}_{1: t}\right)=\prod_{\omega=1}^{\Omega} p\left(\mathbf{y}_{t+\omega} \mid \mathbf{y}_{1: t}, X_{t+\omega}^{(i)}, i=1, \ldots, N\right)\).
- challenge : How to design NN that incorporate historical observations \(\mathbf{y}_{1: t}\) & covariates \(X_{t+\omega}^{(i)}\)
2-1. NN architecture
use both information… \(y_{t}^{(i)}=\nu_{B}\left(X_{t}^{(i)}\right)+n_{t}^{(i)}\).
- 1) past observation
- 2) exogenous variables
to extend dynamic regression to multiple t.s forecasting scenario…
\(\rightarrow\) propose a variant of residual NN
Main difference from original ResNet : new block allows for 2 inputs
- 1) one for historical observation
- 2) one for exogenous variables
propose DeepTCN
- high-level architecture is similar to Seq2Seq framework
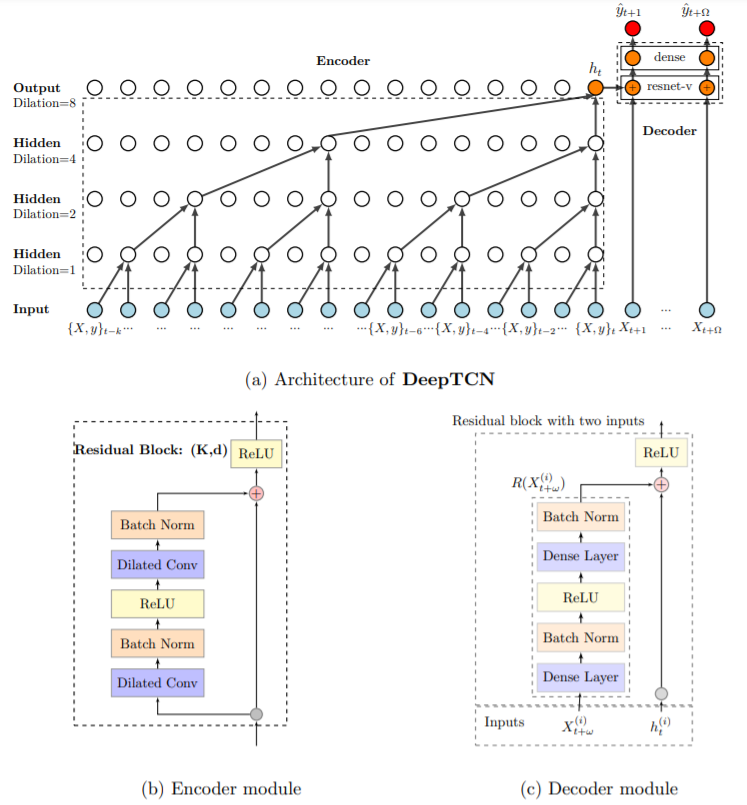

2-2. Encoder : Dilated Causal Convolutions
- use inputs, no later than \(t\)
- use skipping
- notation : \(s(t)=\left(x *_{d} w\right)(t)=\sum_{k=0}^{K-1} w(k) x(t-d \cdot k)\).
- stacking multiple Dilated Causal Convolutions :
- enable networks to have very LARGE receptive fields &
- capture LONG-range temporal dependencies with smaller number of layers
- Figure 1-a)
- \(d\) =\(\{1,2,4,8\}\)
- \(K\)=2
- receptive filed of size \(16\)
2-3. Decoder : Residual Neural Network
decoder includes 2 parts..
-
1) variant of residual neural network ( = resnet-v )
-
2) dense layer
- maps output of 1) into probabilistic forecast
-
notation : \(\delta_{t+\omega}^{(i)}=R\left(X_{t+\omega}^{(i)}\right)+h_{t}^{(i)}\)
- \(h_{t}^{(i)}\) : latent output of encoder
- \(X_{t+\omega}^{(i)}\) : future covariates
- \(\delta_{t+\omega}^{(i)}\) : latent output of resnet-v
- \(R(\cdot)\) : residual function
-
output dense layer maps the latent variable \(\delta_{t+\omega}^{(i)}\) to produce the final output \(Z\)
( = probabilistic estimation of interest )
2-4. Probabilistic forecasting framework
- output dense layer produce \(m\) outputs : \(Z=\left(z^{1}, \ldots, z^{m}\right)\)
- 2 outputs : ( mean & std ) \(Z_{t+\omega}^{(i)}=\left(\mu_{t+\omega}^{(i)}, \sigma_{t+\omega}^{(i)}\right)\).
- probabilistic forecast : \(P\left(y_{t+\omega}^{(i)}\right) \sim G\left(\mu_{t+\omega}^{(i)}, \sigma_{t+\omega}^{(i)}\right)\).
1) Non-parametric approach
- forecasts can be obtained by quantile regression
- quantile loss : \(L_{q}\left(y, \hat{y}^{q}\right)=q\left(y-\hat{y}^{q}\right)^{+}+(1-q)\left(\hat{y}^{q}-y\right)^{+}\)
- where \((y)^{+}=\max (0, y)\) and \(q \in(0,1)\)
- minimize the total quantile loss :
- \(L_{Q}=\sum_{j=1}^{m} L_{q_{j}}\left(y, \hat{y}^{q_{j}}\right)\).
2) Parametric approach
-
MLE (Maximum Likelihood Estimation)
-
loss function : negative log-likelihood
\(\begin{aligned} L_{G} &=-\log \ell(\mu, \sigma \mid y) \\ &=-\log \left(\left(2 \pi \sigma^{2}\right)^{-1 / 2} \exp \left[-(y-\mu)^{2} /\left(2 \sigma^{2}\right)\right]\right) \\ &=\frac{1}{2} \log (2 \pi)+\log (\sigma)+\frac{(y-\mu)^{2}}{2 \sigma^{2}} \end{aligned}\).
2-5. Input Features
2 kinds of input features
- 1) time DEPENDENT
- ex) product price, day of week
- 2) time INDEPENDENT
- ex) product id, product brand, category
To capture seasonality..
- use “hour-of-the day, day-of-the-week….”
