(paper) Probabilistic Forecasting of Sensory Data with Generative Adversarial Networks (ForGAN)

Probabilistic Forecasting of Sensory Data with Generative Adversarial Networks - ForGAN (2019)

Contents

1. Abstract
2. Methodology
   1. GAN
   2. CGAN
   3. Probabilistic Forecasting with CGAN

0. Abstract

ForGAN

• one step ahead probabilistic forecasting, with GAN
• utilizes the power of
  • conditional GAN to learn data generating distn
  • and compute probabilistic forecasts from it

1. Methodology

(1) GAN

\(\begin{aligned} \min _{G} \max _{D} V(D, G)=& \mathbb{E}_{x \sim \rho_{\text {data }}(x)}[\log D(x)]+ \mathbb{E}_{z \sim \rho_{\text {noise }}(z)}[\log (1-D(G(z)))] \end{aligned}\).

(2) CGAN

\(\begin{aligned} \min _{G} \max _{D} V(D, G)=& \mathbb{E}_{x \sim \rho_{\text {data }}(x)}[\log D(x \mid y)]+ \mathbb{E}_{z \sim \rho_{z}(z)}[\log (1-D(G(z \mid y)))] \end{aligned}\).

(3) Probabilistic Forecasting with CGAN

aim to model the probability distn of one step ahead value \(x_{t+1}\) ,given the historical data \(c=\left\{x_{0}, . ., x_{t}\right\}\)

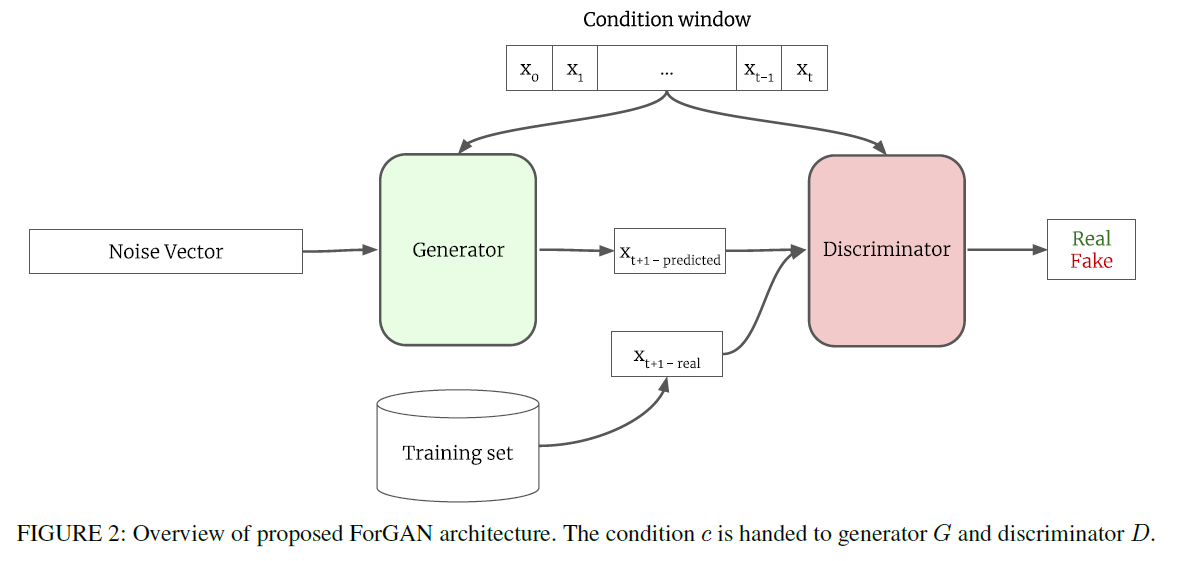
• historical data is provided to both G & D
  • \(G\) : takes noise vector \(\sim N(0,1)\) & forecasts with regard to context window \(c\)
  • \(D\) : takes \(x_{t+1}\) and inspects whether it is valid value to follow \(c\) or not

\[\begin{aligned} \min _{G} \max _{D} V(D, G)=& \mathbb{E}_{x_{t+1} \sim \rho_{\text {data }}\left(x_{t+1}\right)}\left[\log D\left(x_{t+1} \mid c\right)\right]+\mathbb{E}_{z \sim \rho_{z}(z)}[\log (1-D(G(z \mid c)))] \end{aligned}\]