(paper) Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting

Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting (2020)

Contents

1. Abstract
2. Introduction
3. Background
   1. Problem Definition
   2. Transformer
4. Methodology
   1. Enhancing the locality of Transformer
   2. Breaking the memory bottleneck of Transformer

0. Abstract

propose to tackle forecasting problem with TRANSFORMER

2 major weakness

• 1) locality-agnostic
  • insensitive to local context
  • prone to anomalies
• 2) memory-bottleneck
  • space complexity grows quadratically with sequence length \(L\)

\(\rightarrow\) propose LogSparse Transformer ( ONLY \(O(L(\log L)^2)\) memory cost )

1. Introduction

Transformer : leverages attention mechanism to process a sequence of data ( regardless of distance )

HOWEVER….

• canonical dot-product self-attention matches queries against keys insensitive to local context
• space complexity of canonical Transformer grows quadratically with input length \(L\)

Contribution

• 1) apply Transformer architecture to time series forecasting

• 2) propose convolutional self-attention, by employing causal convolutions

• 3) propoes LogSparse Transformer

2. Background

(1) Problem Definition

• \(N\) related univariate time series \(\left\{\mathbf{z}_{i, 1: t_{0}}\right\}_{i=1}^{N}\)

  ( where \(\mathbf{z}_{i, 1: t_{0}} \triangleq\left[\mathbf{z}_{i, 1}, \mathbf{z}_{i, 2}, \cdots, \mathbf{z}_{i, t_{0}}\right]\) and \(\mathbf{z}_{i, t} \in \mathbb{R}\) : value of time series \(i\) at time \(t^{1}\) )

• \(\left\{\mathrm{x}_{i, 1: t_{0}+\tau}\right\}_{i=1}^{N}\) : associated time-based covariate vectors

  ( known over entire time )

Goal : predict the next \(\tau\) time steps ( \(\left\{\mathbf{z}_{i, t_{0}+1: t_{0}+\tau}\right\}_{i=1}^{N}\) )

• \(p\left(\mathbf{z}_{i, t_{0}+1: t_{0}+\tau} \mid \mathbf{z}_{i, 1: t_{0}}, \mathbf{x}_{i, 1: t_{0}+\tau} ; \boldsymbol{\Phi}\right)=\prod_{t=t_{0}+1}^{t_{0}+\tau} p\left(\mathbf{z}_{i, t} \mid \mathbf{z}_{i, 1: t-1}, \mathbf{x}_{i, 1: t} ; \Phi\right)\).

  ( reduce the problem to learning a one-step-ahead prediction )

To use both observation(\(z\)) & covariates(\(x\))…

• concatenate them to obtain an augmented matrix
• \(\mathbf{y}_{t} \triangleq\left[\mathbf{z}_{t-1} \circ \mathbf{x}_{t}\right] \in \mathbb{R}^{d+1}, \quad \mathbf{Y}_{t}=\left[\mathbf{y}_{1}, \cdots, \mathbf{y}_{t}\right]^{T} \in \mathbb{R}^{t \times(d+1)}\).

Appropriate model \(\mathrm{z}_{t} \sim f\left(\mathbf{Y}_{t}\right)\) :

• predict the distribution of \(\mathbf{z}_{t}\) given \(\mathbf{Y}_{t}\).
• \(f\) : TRANSFORMER

(2) Transformer

\(\mathbf{O}_{h}=\operatorname{Attention}\left(\mathbf{Q}_{h}, \mathbf{K}_{h}, \mathbf{V}_{h}\right)=\operatorname{softmax}\left(\frac{\mathbf{Q}_{h} \mathbf{K}_{h}^{T}}{\sqrt{d_{k}}} \cdot \mathbf{M}\right) \mathbf{V}_{h}\).

• \(\mathbf{M}\) : upper triangular elements
• \(\mathbf{O}_{1}, \mathbf{O}_{2}, \cdots, \mathrm{O}_{H}\) are concatenated and linearly projected
• then, FFNN

3. Methodology

(1) Enhancing the locality of Transformer

patterns in times

• ex) holidays, extreme weather ( = anomaly )

\(\rightarrow\) in self-attention layers of canonical Transformer,

the similarities between Q & K are computed based on their point-wise values, without fully leveraging local context like shape

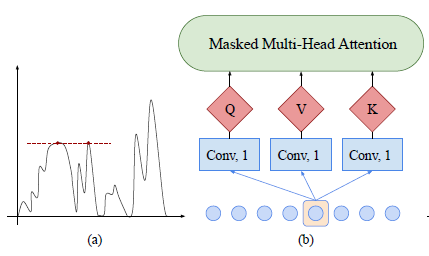
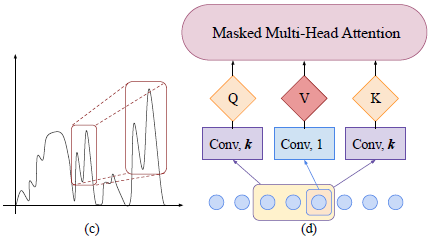
Propose convolutional self-attention to solve the problem!

• employ causal convolution ( kernel size=\(k\), stride=1 )
• no access to future information

(2) Breaking the memory bottleneck of Transformer

• \(O(L^2)\) memory usage for sequence with length \(L\)

• propose LogSparse Transformer :

  • only need to calculate \(O(\log L)\) dot products for each cell in each layer
  • only need to stack up \(O(\log L)\) layers

  \(\rightarrow\) total cost of memory usage : \(O(L(\log L)^2)\)

Local Attention

• allow each cell to densely attend to cells in its left window of size \(O(\log_2 L)\)
• more local information

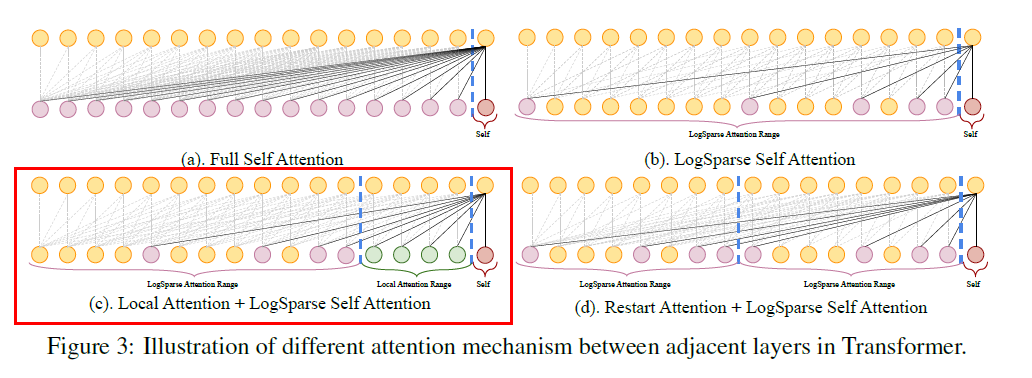
Restart Attention

• divide the whole input with length \(L\) into subsequences
• for each of them, apply LogSparse

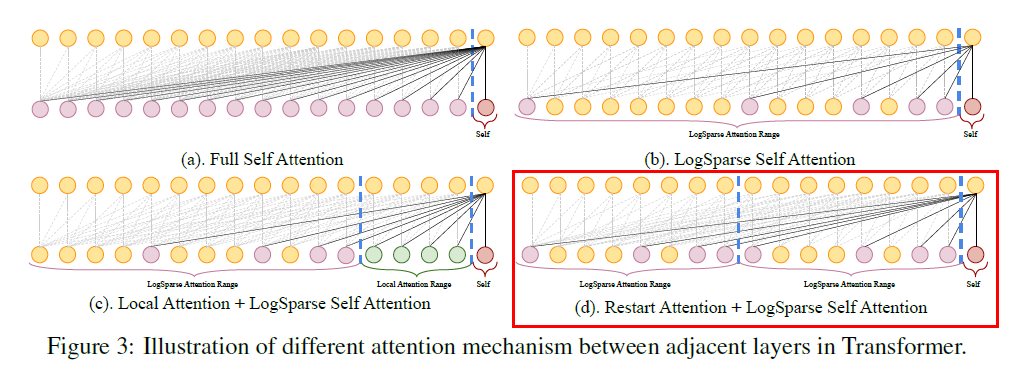
Employing local attention and restart attention won’t change the complexity of our sparse attention strategy, but will create more paths and decrease the required number of edges in the path