FFT with Python

FFT with Python

참고 : https://www.youtube.com/watch?v=fMqL5vckiU0&list=PL-wATfeyAMNrtbkCNsLcpoAyBBRJZVlnf

1. Import Packages

import os
import matplotlib.pyplot as plt
import librosa, librosa.display
import IPython.display as ipd
import numpy as np

2. Listen to Sound

BASE_FOLDER = # xxxxxx
violin_sound_file = "violin_c.wav"
piano_sound_file = "piano_c.wav"
sax_sound_file = "sax.wav"
noise_sound_file = "noise.wav"

ipd.Audio(os.path.join(BASE_FOLDER, sax_sound_file)) 

3. Load Sounds

violin_c4, sr = librosa.load(os.path.join(BASE_FOLDER, violin_sound_file))
piano_c5, _ = librosa.load(os.path.join(BASE_FOLDER, piano_sound_file))
sax_c4, _ = librosa.load(os.path.join(BASE_FOLDER, sax_sound_file))
noise, _ = librosa.load(os.path.join(BASE_FOLDER, noise_sound_file))

4. FFT

FFT using np.fft.fft

X = np.fft.fft(violin_c4)

# 59772
len(violin_c4)== len(X)

• DFT: set # of frequency bins = # of samples

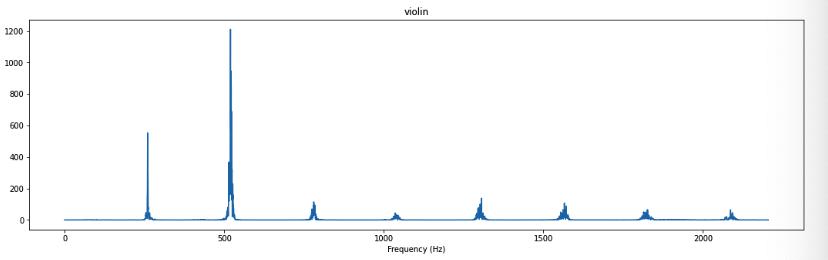
4. Visualize Spectrum

def plot_magnitude_spectrum(signal, sr, title, f_ratio=1):
    X = np.fft.fft(signal)
    X_mag = np.absolute(X)
    
    plt.figure(figsize=(18, 5))
    
    f = np.linspace(0, sr, len(X_mag))
    f_bins = int(len(X_mag)*f_ratio)  
    
    plt.plot(f[:f_bins], X_mag[:f_bins])
    plt.xlabel('Frequency (Hz)')
    plt.title(title)

#plot_magnitude_spectrum(violin_c4, sr, "violin", 1.0)
#plot_magnitude_spectrum(violin_c4, sr, "violin", 0.5)
plot_magnitude_spectrum(violin_c4, sr, "violin", 0.1)