MFCCs with Python

MFCCs with Python

참고 : https://www.youtube.com/watch?v=fMqL5vckiU0&list=PL-wATfeyAMNrtbkCNsLcpoAyBBRJZVlnf

1. Import Packages & Datasets

import librosa
import librosa.display
import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy as np

audio_file = "audio/debussy.wav"
signal, sr = librosa.load(audio_file)

2. Extract MFCCs

mfccs = librosa.feature.mfcc(y=signal, n_mfcc=13, sr=sr)
print(mfccs.shape)

(13, 1292)

• 13 coefficients
• 1292 frames

3. Visualization

plt.figure(figsize=(25, 10))
librosa.display.specshow(mfccs, 
                         x_axis="time", 
                         sr=sr)
plt.colorbar(format="%+2.f")
plt.show()

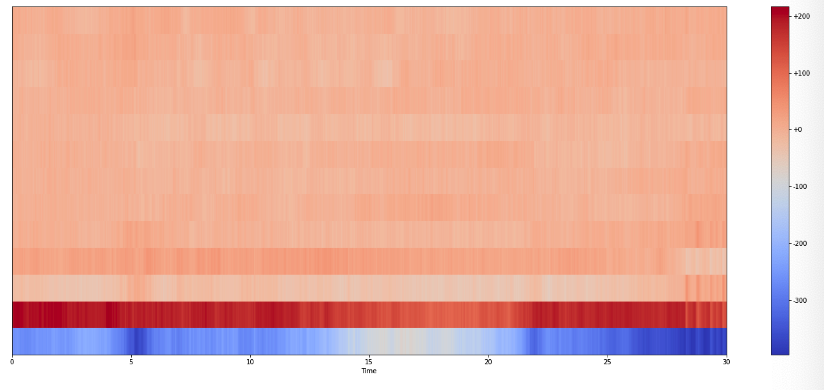
4. \(\Delta\) and \(\Delta \Delta\) MFCCs

delta_mfccs = librosa.feature.delta(mfccs)
delta2_mfccs = librosa.feature.delta(mfccs, order=2)

First derivative

plt.figure(figsize=(25, 10))
librosa.display.specshow(delta_mfccs, 
                         x_axis="time", 
                         sr=sr)
plt.colorbar(format="%+2.f")
plt.show()

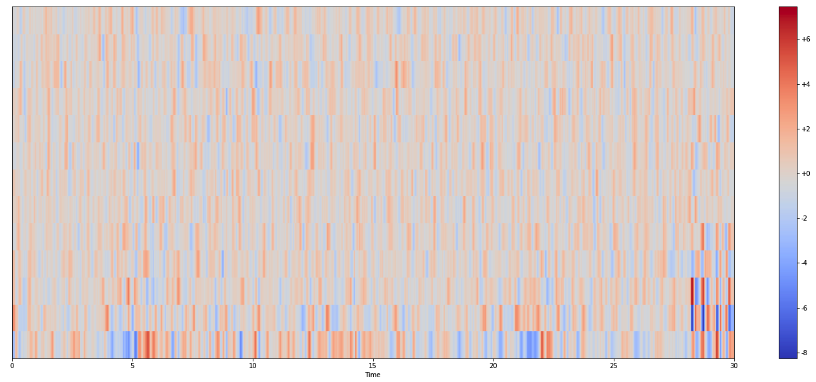
Second derivative

plt.figure(figsize=(25, 10))
librosa.display.specshow(delta2_mfccs, 
                         x_axis="time", 
                         sr=sr)
plt.colorbar(format="%+2.f")
plt.show()

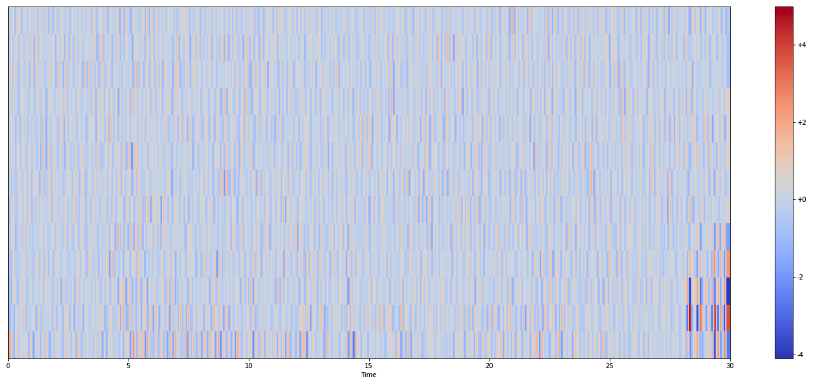
5. Get MFCC features

Concatenate “original” & “first” derivative & “second” derivative

mfccs_features = np.concatenate((mfccs, delta_mfccs, delta2_mfccs))
print(mfccs_features.shape)

(39,1292)