Melspectogram

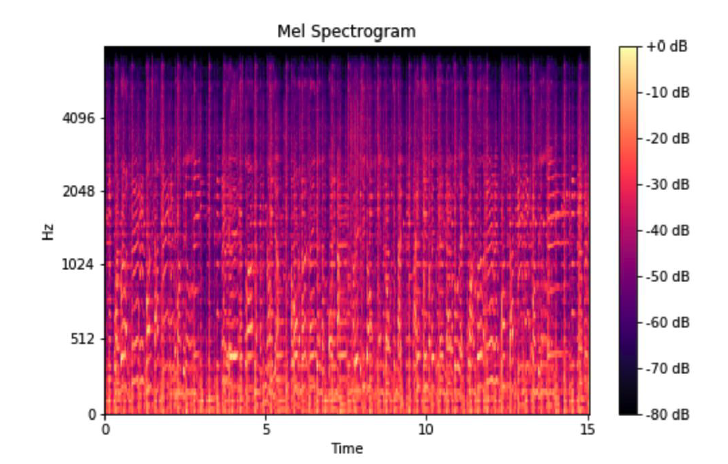
Melspectogram

참고 : https://www.youtube.com/watch?v=fMqL5vckiU0&list=PL-wATfeyAMNrtbkCNsLcpoAyBBRJZVlnf

1. Pyschoacoustic expriment

Pair 1

• a) 64Hz
• b) 262Hz

Pair 2

• a) 1568 Hz
• b) 1760 Hz

Even though both pairs have about 200 Hz difference..

\(\rightarrow\) If we listen to them … Diff( 1(a) , 1(b) ) » Pair ( 2(a), 2(b) )

\(\rightarrow\) Humans perceive frequency LOGARITHMICALLY

2. Ideal Audio Feature

(1) Time-frequency representation

(2) Perceptually-relevant amplitude representation

(3) Perceptually-relevant frequency representation

\(\rightarrow\) use Melspectograms

3. Mel-scale

Key Points

• Logarithmic scale of frequency
• Equal distances on the scale have same PERCEPTUAL distance
• 1000 Hz = 1000 Mel

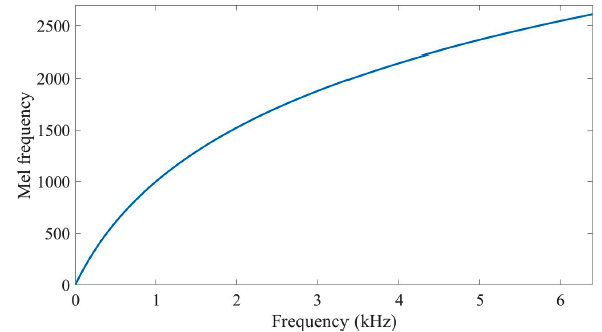
(1) Frequency (Hz) \(\rightarrow\) Mel-Frequency

• \[m=2595 \cdot \log_{10} \left(1+\frac{f}{700}\right)\]

(2) Mel-Frequency \(\rightarrow\) Frequency (Hz)

• \(f=700\left(10^{m / 2595}-1\right)\).

4. How to get Melspectogram?

Step 1) Extract STFT

Step 2) Convert “amplitude” to “DBs”

Step 3) Convert “frequencies” to “Mel scale”

(1) Frequency \(\rightarrow\) Mel scale

Step 3-1) Choose the number of mel bands

• how many to choose? 40/60/90/128? … It depends on the problem!

Step 3-2) Construct mel filter banks

Step 3-3) Apply mel filter banks to spectogram

(2) Mel-filter banks

Step 3-2) Construct mel filter banks

• step a) convert LOWEST & HIGHEST frequency to Mel-frequency
• step b) create # of bands equally spaced points
• step c) convert back to Hz
• step d) round to nearest frequency bin
• step e) create triangular filters

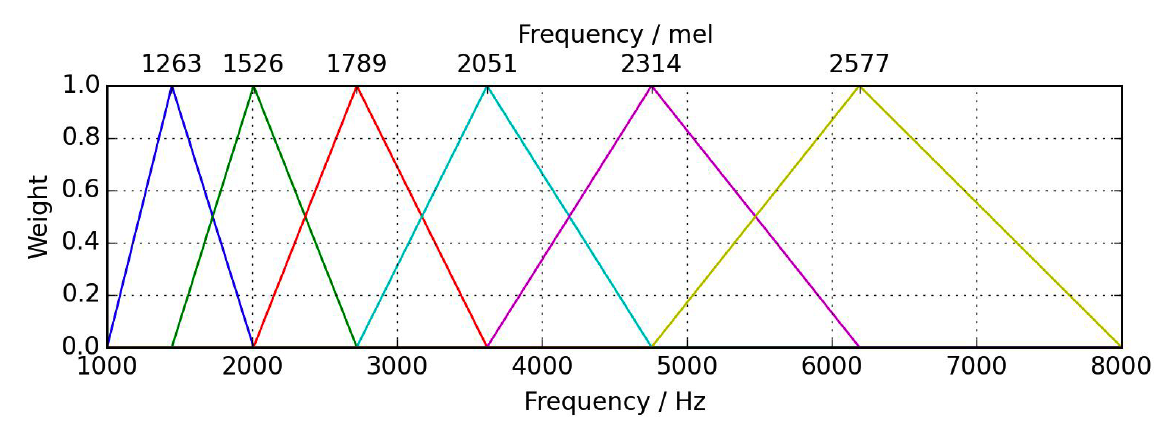
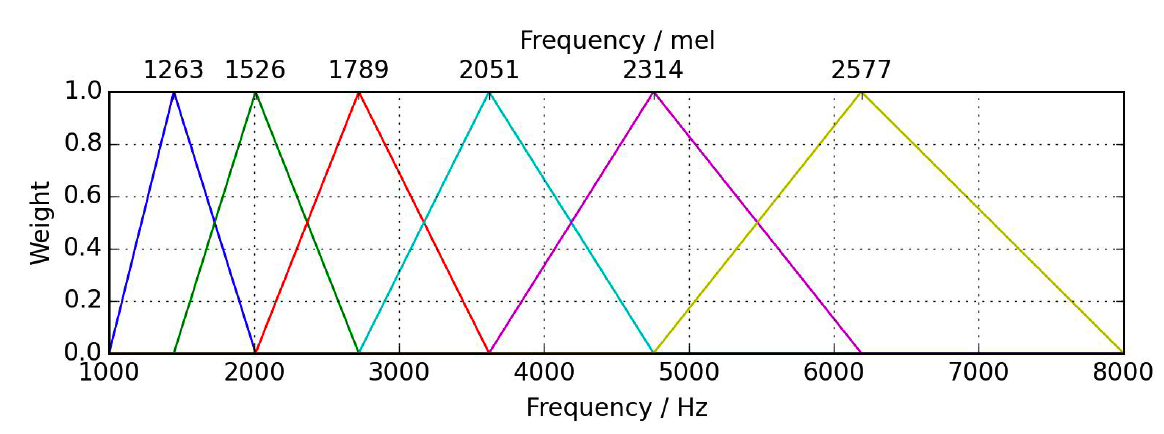
with Python

import numpy as np
import matplotlib.pyplot as plt

def Hz2Mel(f):
    mel = 2595*np.log10(1+(f/700))
    return mel

def Mel2Hz(mel):
    hz = 700*(10**(mel/2595)-1)
    return hz

num_bands = 6
equal_space_mel = np.linspace(min_mel,max_mel,num_bands)
equal_space_Hz = Mel2Hz(equal_space_mel)

plt.plot(x_Hz,y_mel)
plt.axhline(min_mel,color='red')
plt.axhline(max_mel,color='red')
for mel in equal_space_mel[1:-1]:
    plt.axhline(mel,color='orange')

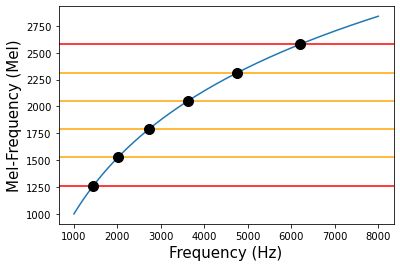
for hz,mel in zip(equal_space_Hz,equal_space_mel):
    plt.plot(hz, mel, marker="o",markersize=10,color='black')
plt.xlabel("Frequency (Hz)",size=15)
plt.ylabel("Mel-Frequency (Mel)",size=15)

Applying Mel fitler bank \(M\) to spectogram \(Y\)

Melspectogram = \(MY\)

• Shape of \(M\) : ( # of bands, \(\frac{\text{frame size}}{2}\) + 1 )
• Shape of \(Y\) : ( \(\frac{\text{frame size}}{2}\) + 1 , # of frames )

\(\rightarrow\) Shape of \(MY\) : ( # of bands, # of frames )