TimeSiam; A Pre-Training Framework for Siamese Time-Series Modeling

TimeSiam: A Pre-Training Framework for Siamese Time-Series Modeling

( SimMTM 저자 )

https://arxiv.org/pdf/2402.02475.pdf

Contents

1. Abstract
2. Introduction
3. TimeSiam
   1. Pre-training
   2. Fin-tuning
4. Experiments

Abstract

Randomly masking TS or calculating series-wise similarity

\(\rightarrow\) Neglect inherent temporal correlations

Time-Siam

• TS + Siamese Network

• Pretrains siamese encoders to capture intrinsic temporal correlations between

  randomly sampled (1) past and (2) current subseries

• Simple DA (e.g. masking)
• Benefit from diverse augmented subseries and learn internal time-dependent representations through a past-to-current reconstruction
• Learnable lineage embeddings
  • To distinguish temporal distance between sampled series
  • To foster the learning of diverse temporal correlations
• Experiments) Forecasting and Classification
  • across 13 standard benchmarks in both intra- and cross-domain scenarios.

1. Introduction

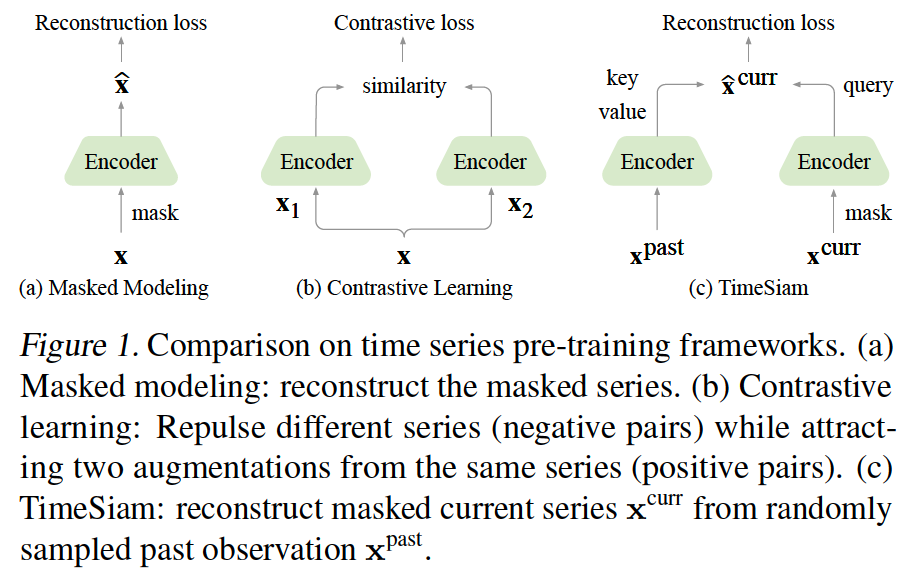
Two paradigms

• (1) Masked modeling
  • Randomly masking a portion of time points will seriously distort vital temporal correlations of time series (Dong et al. (2023))
• (2) Contrastive learning
  • Excels in instance-level representation learning
  • Limitation: Reliance on augmentations to learn useful invariances (Xiao et al., 2020)
  • May fail in capturing fine-grained temporal variations

Critical point of TS pre-training is optimizing encoders to accurately capture temporal correlations

TimeSiam

• Simple yet effective self-supervised pre-training framework

• [Figure 1-(c)] Sample pairs of subseries across different timestamps from the same TS

  ( = “Siamese subseries” )

• Leverages Siamese networks to capture correlations between temporally distanced subseries

• Simple data augmentation

• Not constrained by proximity information in TS

• Effectively model the correlation among distanced subseries
  • empowers the model with a more thorough understanding of the whole TS

2. TimeSiam

Past-to-current reconstruction task with simple masked augmentation

( + Learnable lineage embeddings : to dynamically capture the disparity among different distanced subseries pairs )

(1) Pre-training

Two modules

• (1) Siamese subseries sampling
• (2) Siamese modeling

a) Siamese Subseries Sampling

• (Previous) Solely on modeling the individual series itself
  • neglecting the inherent correlations among temporally related TS
• (TimeSiam) Focus on modeling temporal correlations of subseries across different timestamps
  • capturing the intrinsic time-correlated information of TS

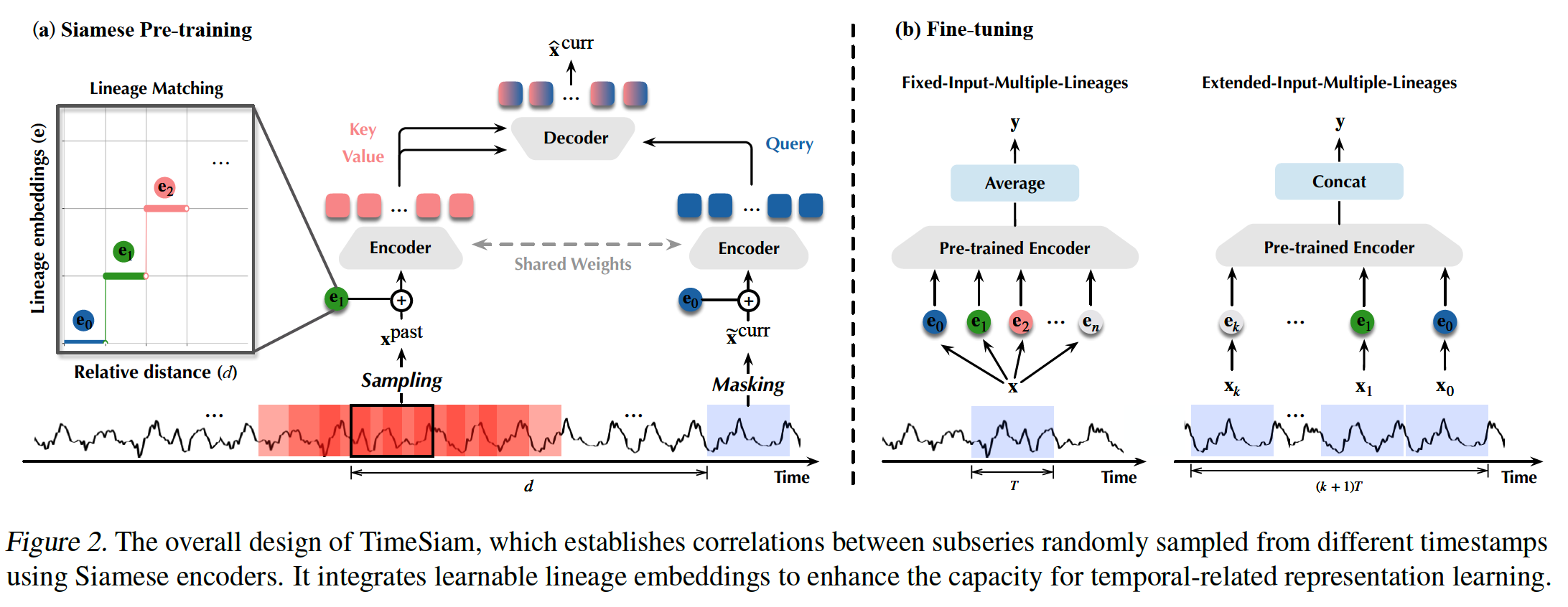
• “Siamese subseries” ( = Subseries pairs )
  • By randomly sampling a past sample \(\mathrm{x}^{\text {past }}\) preceding the current sample \(\mathbf{x}^{\text {curr }}\) in the same TS
    • Each contains \(T\) timestamps and \(C\) observed variables
• Goal: Constructing correlations and capturing temporal variations between these Siamese subseries
• Relative distance between the past and current subseries : \(d\)
• Simple masking augmentation
  • To generate augmented current subseries \(\widetilde{\mathbf{x}}^{\text {curr }}\) that further improves the diversity and the disparity of Siamese subseries pairs
• \(\left(\mathrm{x}^{\text {past }}, \widetilde{\mathrm{x}}^{\text {curr }}\right)=\text { Mask-Augment }\left(\left(\mathrm{x}^{\text {past }}, \mathrm{x}^{\text {curr }}\right)\right)\).

b) Siamese Modeling

Lineage embeddings

• Integrate learnable lineage embeddings during pre-training

  • to effectively capture the disparity among different Siamese pairs

  • enhance the model’s capacity to extract diverse temporal-related representations

• Used to identify the temporal distance between Siamese subseries

• \(N\) learnable lineage embeddings \(\left\{\mathbf{e}_i^{\text {lineage }}\right\}_{i=1}^N\)

  • \(\mathbf{e}_i^{\text {lineage }} \in \mathbb{R}^{1 \times D}\),

Lineage embeddings for PAST & CURRENT

• For the past sample \(\mathrm{x}^{\text {past }}\)…
  • apply the LineageMatching \((\cdot)\)
  • to dynamically match a certain lineage embedding based on its temporal distance \(d\) to the current series
• For the current sample \(\widetilde{\mathbf{x}}^{\text {curr }}\)…
  • use a special lineage embedding to represent a degeneration situation as \(d=0\)

\(\begin{aligned} \mathbf{e}_i^{\text {lineage }} & =\operatorname{LineageMatching}(d) \\ \mathbf{z}^{\text {past }} & =\operatorname{Embed}\left(\mathbf{x}^{\text {past }}\right) \oplus \mathbf{e}_i^{\text {lineage }} \\ \widetilde{\mathbf{z}}^{\text {curr }} & =\operatorname{Embed}\left(\widetilde{\mathbf{x}}^{\text {curr }}\right) \oplus \mathbf{e}_0^{\text {lineage }} \end{aligned}\).

• where \(\mathbf{e}_0^{\text {lineage }} \in \mathbb{R}^{1 \times D}\) is the specific embedding for current subseries
• \(\mathbf{z}^{\text {past }}, \widetilde{\mathbf{z}}^{\text {curr }} \in \mathbb{R}^{T \times D}\) .

Utilizes Siamese encoders

• can be instantiated as advanced TS models
  • e.g. PatchTST (Nie et al., 2023) or iTransformer (Liu et al., 2024).

• \(\mathbf{h}_e^{\text {past }}=\operatorname{Encoder}\left(\mathbf{z}^{\text {past }}\right)\).

• \(\widetilde{\mathbf{h}}_e^{\text {curr }}=\operatorname{Encoder}\left(\widetilde{\mathbf{z}}^{\text {curr }}\right)\).

​ where \(\mathbf{h}_e^{\text {past }}, \tilde{\mathbf{h}}_e^{\text {curr }} \in \mathbb{R}^{T \times D}\)

Past-to-current reconstruction task

• Use a decoder that integrates cross-attention and self-attention
  • to incorporate past information into the current subseries for reconstruction
• \(\widetilde{\mathbf{h}}_e^{\text {curr }}\) : query
• \(\mathbf{h}_e^{\text {past }}\) : key and value

\(\mathbf{h}_d=\operatorname{Decoder}\left(\widetilde{\mathbf{h}}_e^{\text {curr }}, \mathbf{h}_e^{\text {past }}\right)\).

• Generate the decoder representation of the current time subseries, denotes as \(\widehat{\mathbf{h}}_d\).

• \(\begin{aligned} \widehat{\mathbf{h}}_d & =\operatorname{LayerNorm}\left(\widetilde{\mathbf{h}}_e^{\text {curr }}+\operatorname{Cross-Attn}\left(\widetilde{\mathbf{h}}_e^{\text {curr }}, \mathbf{h}_e^{\text {past }}, \mathbf{h}_e^{\text {past }}\right)\right) \\ \mathbf{h}_d^{\prime} & =\operatorname{LayerNorm}\left(\widehat{\mathbf{h}}_d+\operatorname{Self-Attn}\left(\widehat{\mathbf{h}}_d, \widehat{\mathbf{h}}_d, \widehat{\mathbf{h}}_d\right)\right. \\ \mathbf{h}_d & =\operatorname{LayerNorm}\left(\mathbf{h}_d^{\prime}+\operatorname{FFN}\left(\mathbf{h}_d^{\prime}\right)\right) . \end{aligned}\).
• Output of the decoder \(\mathbf{h}_d \in \mathbb{R}^{T \times D}\)

Reconstruction:

• \(\widehat{\mathbf{x}}^{\text {curr }}=\operatorname{Projector}\left(\mathbf{h}_d\right)\).
• \(\mathcal{L}_{\text {reconstruction }}= \mid \mid \mathrm{x}^{\text {curr }}-\widehat{\mathbf{x}}^{\text {curr }} \mid \mid _2^2\).

(2) Fine-tuning

Can capture diverse temporal related representations under different lineage embeddings

Two types of fine-tuning paradigms

• (1) Fixed input series setting

• (2) Extended input series setting

Fixed-Input-Multiple-Lineages

• [Standard] Generates only one type of representation

• [TimeSiam] Pretrains Siamese encoders with diverse lineage embeddings to capture different distanced temporal correlations

  \(\rightarrow\) Derive diverse representations with different lineages for the same input series

• Enhances the diversity of extracted representations

• \(\overline{\mathbf{h}}_e=\text { Average }\left(\mathbf{h}_{e, 0}, \mathbf{h}_{e, 1}, \ldots \mathbf{h}_{e, n}\right)\).

  • Ensemble of a set of temporal representations derived from the same input series
  • Input series \(\mathbf{x} \in \mathbb{R}^{T \times C}\),
  • \(\mathbf{h}_{e, i}=\operatorname{Encoder}\left(\operatorname{Embed}(\mathbf{x}) \oplus \mathbf{e}_i^{\text {lineage }}\right)\).

Extended-Input-Multiple-Lineages

Model may receive longer records than the pre-training series

Can leverage multiple lineage embeddings trained under different temporal distanced pairs to different segments

\(\overline{\mathbf{h}}_e=\operatorname{Concat}\left(\mathbf{h}_{e, 0}, \mathbf{h}_{e, 1}, \ldots, \mathbf{h}_{e, k}\right)\).

• where \(\mathbf{h}_{e, i}=\operatorname{Encoder}\left(\operatorname{Embed}\left(\mathbf{x}_i\right) \oplus \mathbf{e}_{\text {LineageMatching }(i T)}^{\text {lineage }}\right)\).
• \(\overline{\mathbf{h}}_e \in \mathbb{R}^{(k+1) T \times D}\) denotes the extracted representation for extended input series.

3. Experiments

• Forecasting & Classification

• In- & Cross-domain setting

(1) Experimental Setup

a) Datasets

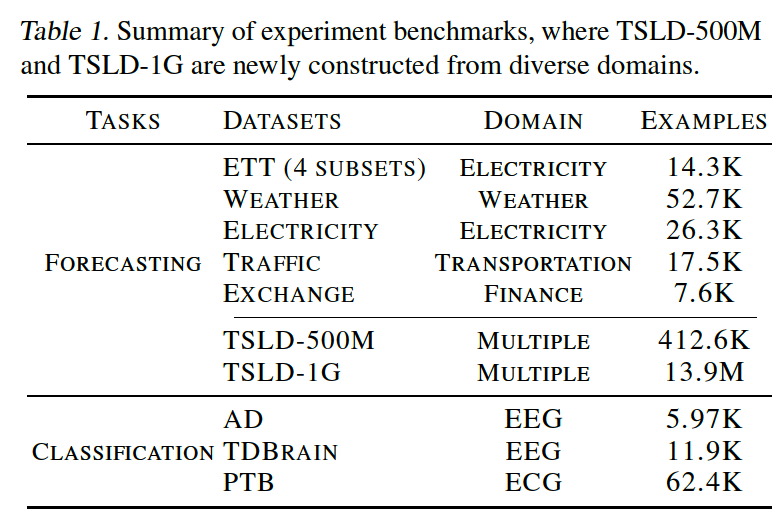
TSLD

• To further demonstrate the pre-training benefits under large and diverse data
• Constructed by merging time series datasets from multiple domains that are nonoverlapping with the other datasets

b) Backbone

• iTransformerr & PatchTST for TS forecasting

• TCN for TS classification

(2) Main Results

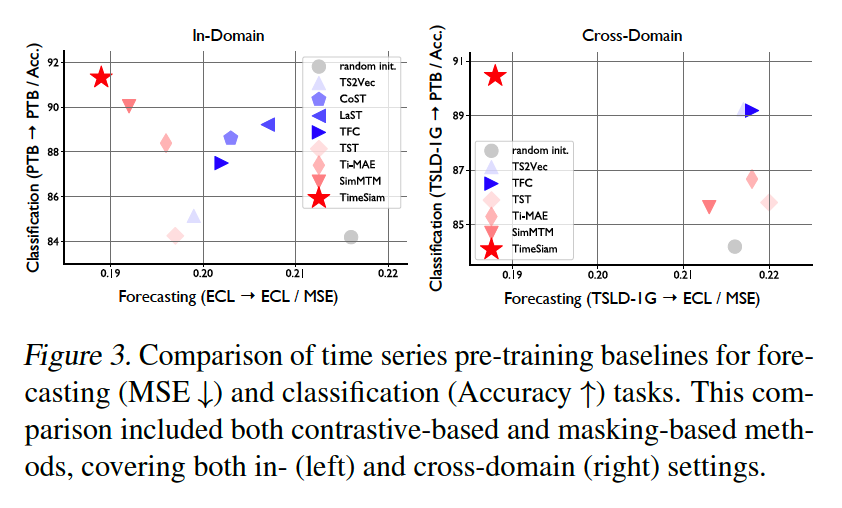
(3) Forecasting

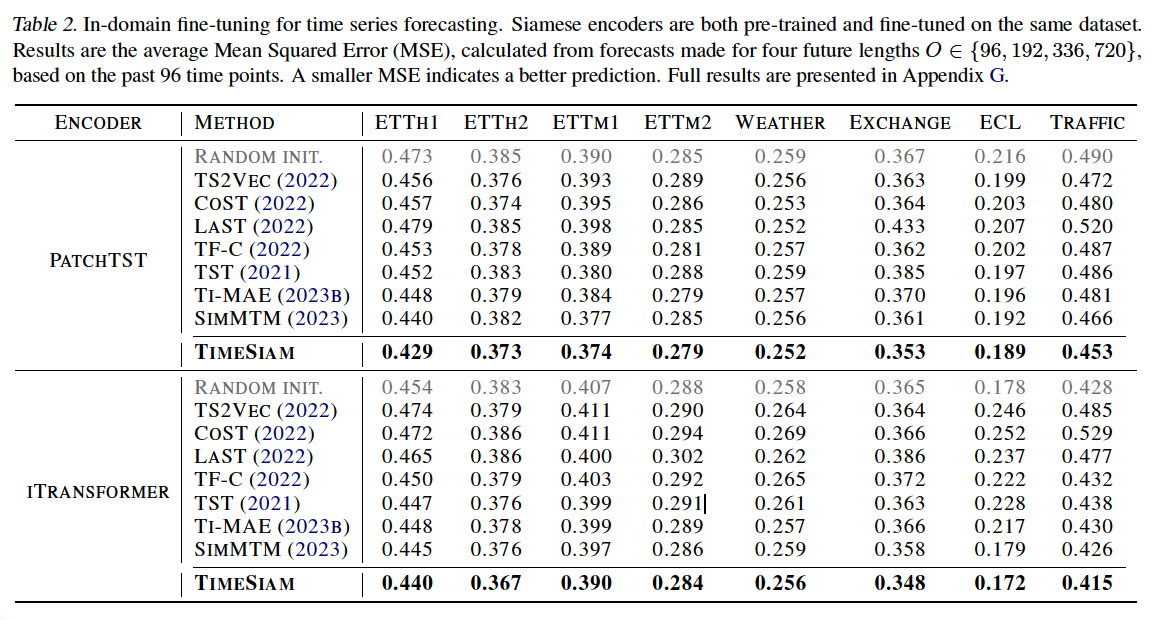
a) In-domain

b) Cross-domain

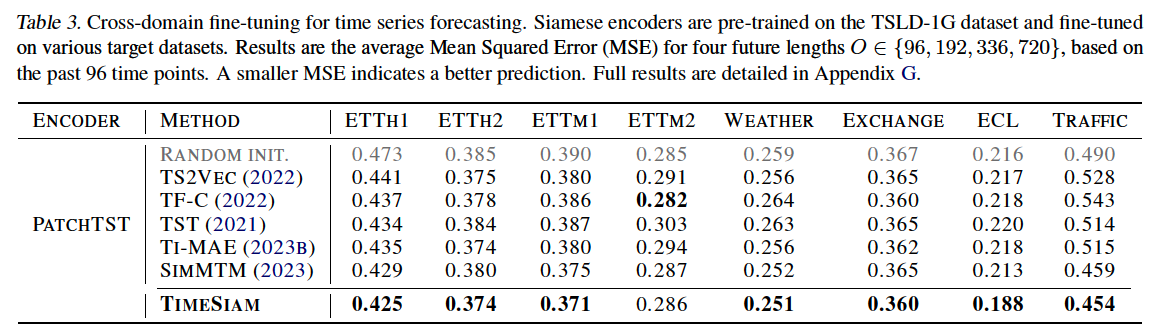
Use the TSLD-1G dataset

• Large-scale TS samples from diverse domains
• Even show superior performance compared to the in-domain scenario in some datasets
  • ex) TSLD-1G → {ETTh1, ETTm1}.

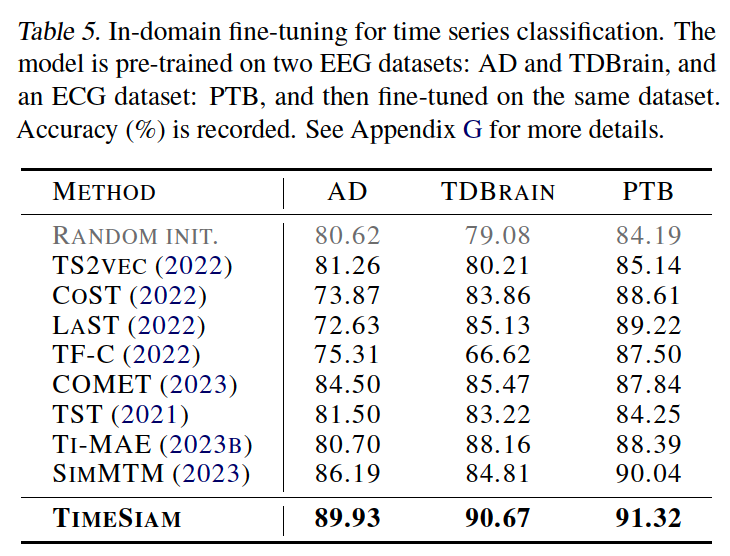
(4) Classification

a) In-domain

<br

b) Cross-domain

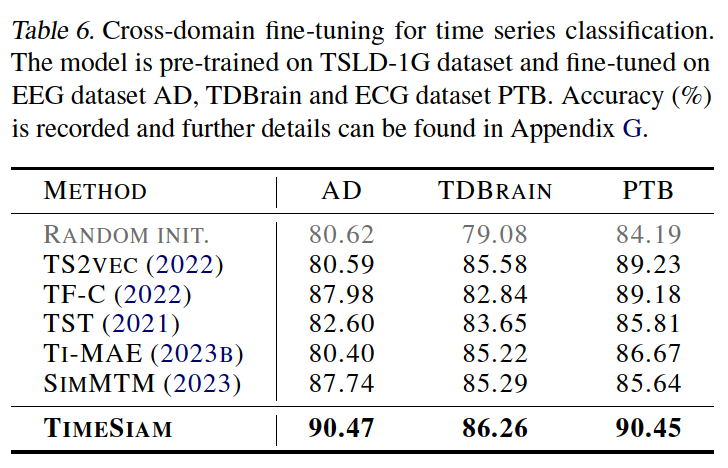
(5) Ablation Studies

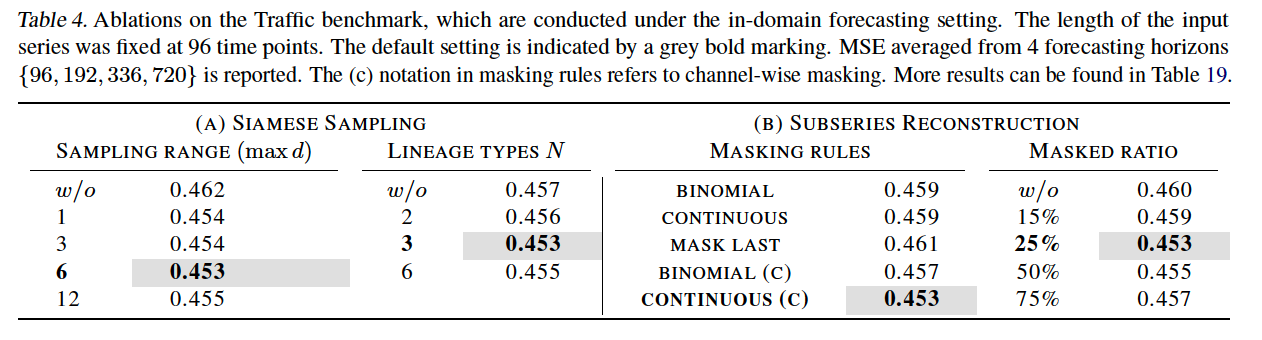
• (c) : channel-wise

(6) Analysis Experiment

a) Data Scale and Model Capacity

b) Adapt to Extended-Length Input

TimeSiam can natively adapt to longer inputs

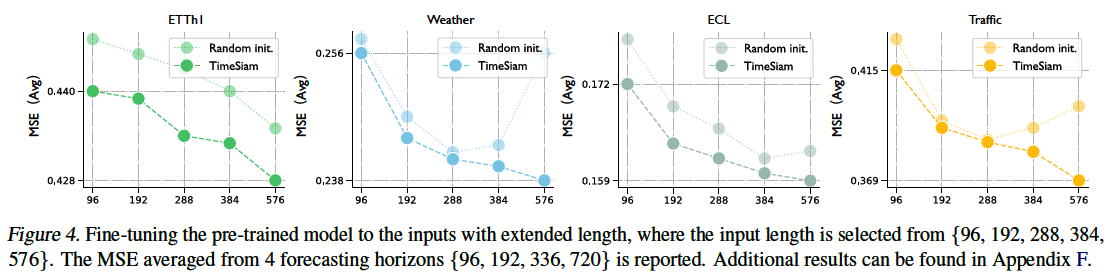
• [Standard] Degenerate under extended input length

c) Linear Probing

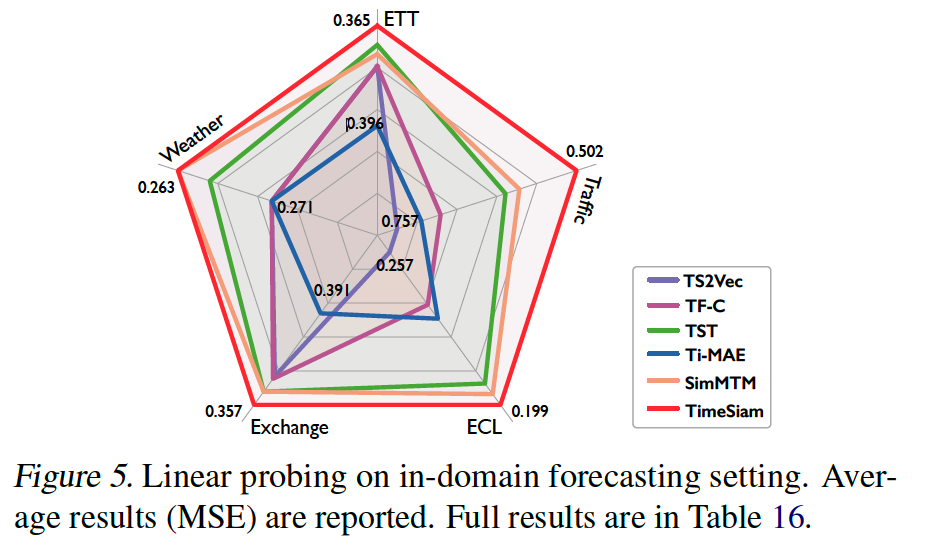
d) Embedding Effectiveness

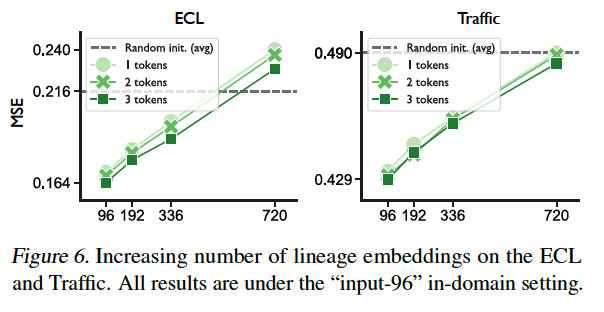
Advantages of employing varying numbers of lineage embeddings

\(\rightarrow\) Incorporation of lineage embeddings enhances prediction performance