Unsupervised Scalable Representation Learning for Multivariate Time Series (2019)
Contents
- Abstract
- Introduction
- Related Works
- Unsupervised Training
- Encoder Architecture
0. Abstract
Time Series의 특징
1) highly variable lengths 2) sparse labeling
\(\rightarrow\) Tackle this challenge, by proposing an UNSUPERVISED method to learn universal embedding of t.s
combine encoder ( based on causal dilated convolutions ) with triplet loss employing “time-based negative sampling”
1. Introduction
topic : unsupervised general-purpose representation learning
problem
- sparsely labeld
- unequal lengths
- scalability & efficiency
propose an unsupervised method to learn general purpose representations for MTS, that comply with the issues of varying and potentially high lengths
2. Related Works
2-1. Unsupervised learning for TS
few recent works tackle unsupervised representation learning for t.s
\(\rightarrow\) These are not scalable, nor suited to long time series
2-2. Triplet Loss
Widely used in various forms for representation learning in different domains
https://blog.kakaocdn.net/dn/mPpjh/btqw78y8fcw/nQlYdKKPbbx6IVABnntduk/img.png
This paper relies on more natural choice of positive samples, learning similarities using “subsampling”
2-3. Convolutional networks for TS
Dilated Convolutions ( ex. WaveNet )
3. Unsupervised Training
seek to train “encoder-only” arcthitecturee
introduce a novel triplet loss time series, inspired by word2vec
proposed triplet loss :
- uses original time-based sampling strategies to overcome the challenge of learning on unlabeled data
Objective
-
ensure that similar t.s obtain similar representations
( with NO supervision to learn such similarity )
Introduce an unsupervised time-based criterion
- take into account t.s with varying length
- Negative Sampling
- use assumption made by CBOW
- representation of the context of a word should probably be, on one hand, close to the one of this word, and on the other hand, distant from the one of randomly chosen word
- (context, word) & (context, random word) to be linearly separable

Notation
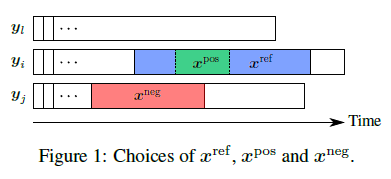
- random subseries \(x^{\text {ref }}\) of a given time series \(y_{i}\)
- representation of \(x^{\text {ref }}\) should be close to the one of any of its subseries \(x^{\text {pos }}\) (a positive example).
- another subseries \(x^{\mathrm{neg}}\) (a negative example) chosen at random (in a different random time series \(\boldsymbol{y}_{j}\) )
- its representation should be distant from the one of \(x^{\text {ref }}\)
- comparison to word2vec
- \(x^{\text {pos }}\) corresponds to a word
- \(x^{\text {ref }}\) to its context
- \(x^{\text {neg }}\) to a random word
- as in word2vec, several negative samples \(\left(\boldsymbol{x}_{k}^{\mathrm{neg}}\right)_{k \in [1, K ]}\), chosen independently at random.
Loss Function
- \(-\log \left(\sigma\left(\boldsymbol{f}\left(\boldsymbol{x}^{\mathrm{ref}}, \boldsymbol{\theta}\right)^{\top} \boldsymbol{f}\left(\boldsymbol{x}^{\mathrm{pos}}, \boldsymbol{\theta}\right)\right)\right)-\sum_{k=1}^{K} \log \left(\sigma\left(-\boldsymbol{f}\left(\boldsymbol{x}^{\mathrm{ref}}, \boldsymbol{\theta}\right)^{\top} \boldsymbol{f}\left(\boldsymbol{x}_{k}^{\mathrm{neg}}, \boldsymbol{\theta}\right)\right)\right)\).
several epochs, picking tuples \(\left(x^{\text {ref }}, x^{\text {pos }},\left(x_{k}^{\text {neg }}\right)_{k}\right)\) at random
Computational Cost
- computational and memory cost : \(\mathcal{O}(K \cdot c(\boldsymbol{f}))\)
- \(c(\boldsymbol{f})\) : the cost of evaluating and backpropagating through \(\boldsymbol{f}\) on a time series
\(\rightarrow\) scalable
4. Encoder Architecture
stacks of exponentially dilated causal convolutions
each layer of network : combination of …
- 1) Causal convolutions
-
- Weight normalizations
-
- Leaky ReLUs
-
- Residual Connections

output of causal network is then given to global max pooling layer, squeezing the temporal dimension & aggregating all temporal information in a fixed sized vector
