Time-LLM; TS Forecasting by Reprogrammming LLM

Time-LLM; Time Series Forecasting by Reprogrammming Large Language Models

Contents

1. Abstract
2. Introduction
3. Related Work
4. Methodology
   1. Model structuere

Abstract

NLP.CV vs. TS

• NLP & CV) single large model can tackle multiple tasks

• TS) specialized

  \(\rightarrow\) Distinct designs for different tasks and applications

Foundation models in TS: has been constrained by data sparsity

TIME-LLM

• Reprogramming framework to repurpose LLMs for general TS forecasting

  ( with the backbone language models kept intact )

• How? by reprogramming the input TS with text prototypes before feeding it into the frozen LLM to align the two modalities.

• Prompt-as-Prefix (PaP)

  • To augment the LLM’s ability to reason with TS data
  • Enriches the input context and directs the transformation of reprogrammed input patches.

• TS patches from the LLM

  • Projected to obtain the forecasts
• Excels in both few-shot and zero-shot learning
• https://github.com/KimMeen/Time-LLM

1. Introduction

Pre-trained foundation models

LLMs’ impressive capabilities have inspired their application to TS forecasting

Several desiderata for leveraging LLMs to advance forecasting

• (1) Generalizability.
  • Capability for few-shot and zero-shot transfer learning
  • Potential for generalizable forecasting across domains without requiring per-task retraining from scratch.
• (2) Data efficiency.
  • Ability to perform new tasks with only a few examples.
  • Enable forecasting for settings where historical data is limited
• (3) Reasoning.
  • Sophisticated reasoning and pattern recognition capabilities
  • Allow making highly precise forecasts by leveraging learned higher-level concepts
• (4) Multimodal knowledge.
  • Gain more diverse knowledge across modalities like vision, speech, and text
  • Enable synergistic forecasting that fuses different data types.
• (5) Easy optimization.
  • Applied to forecasting tasks without learning from scratch.

\(\rightarrow\) Offer a promising path to make time series forecasting more general, efficient, synergistic, and accessible compared to current specialized modeling paradigms.

Key point: effective alignment of the modalities of TS & NLP

\(\rightarrow\) Challenging task, because…

Reason 1)

• (NLP) LLMs operate on discrete tokens
• (TS) Inherently continuous.

Reason 2)

• Knowledge and reasoning capabilities to interpret TS patterns are not naturally present within LLMs’ pre-training.

Time-LLM

Reprogramming framework to adapt LLM for TS forecasting while keeping the backbone model intact.

Corer Idea:

• Reprogram the input TS into text prototype representations

Propose Prompt-as-Prefix (PaP)

• To further augment the model’s reasoning about TS concepts
• Enrich the input TS with additional context and providing task instructions in the modality of natural language.

Output of the LLM

• Projected to generate TS forecasts.

Contribution

• (1) Introduce a novel concept of reprogramming LLM for TS forecasting without altering the pre-trained backbone model.

• (2) Propose a new framework, Timee-LLM

  • encompasses reprogramming the input tS into text prototype representations

    ( that are more natural for the LLM )

  • augment the input context with declarative prompts (e.g., domain expert knowledge and task instructions) to guide LLM reasoning.

• (3) SOTA performance in mainstream forecasting tasks

  • especially in few-shot and zero-shot scenarios

2. Related Work

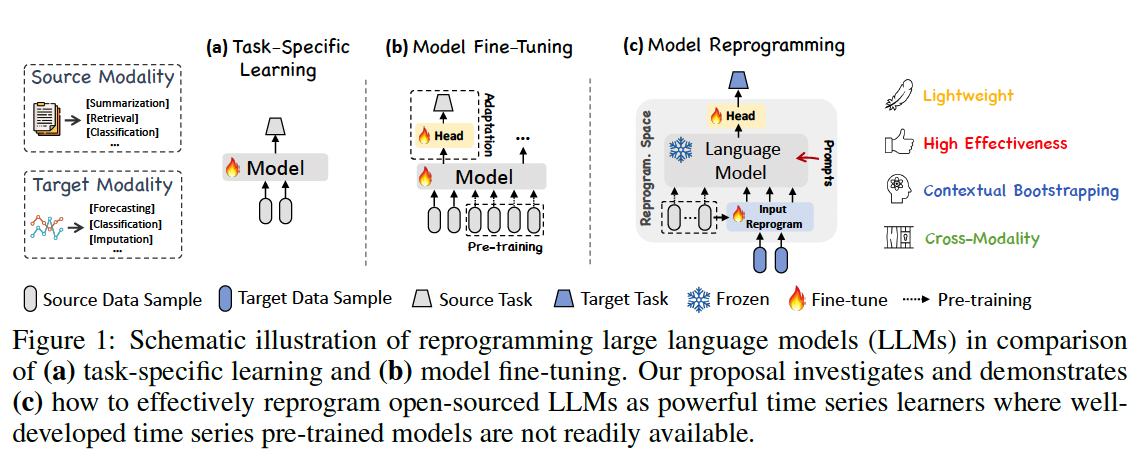
3. Methodology

Goal: Reprogram an embedding-visible language foundation model for general time series forecasting without requiring any fine-tuning of the backbone model.

Notation

• Historical observations: \(\mathbf{X} \in \mathbb{R}^{N \times T}\)
  • \(N\) different 1-dimensional variables across \(T\) time steps.
• LLM: \(f(\cdot)\)
• Goal: forecast \(H\) future time steps ( = \(\hat{\mathbf{Y}} \in \mathbb{R}^{N \times H}\) )

Loss function: \(\frac{1}{H} \sum_{h=1}^H \mid \mid \hat{\mathbf{Y}}_h-\mathbf{Y}_h \mid \mid _F^2\).

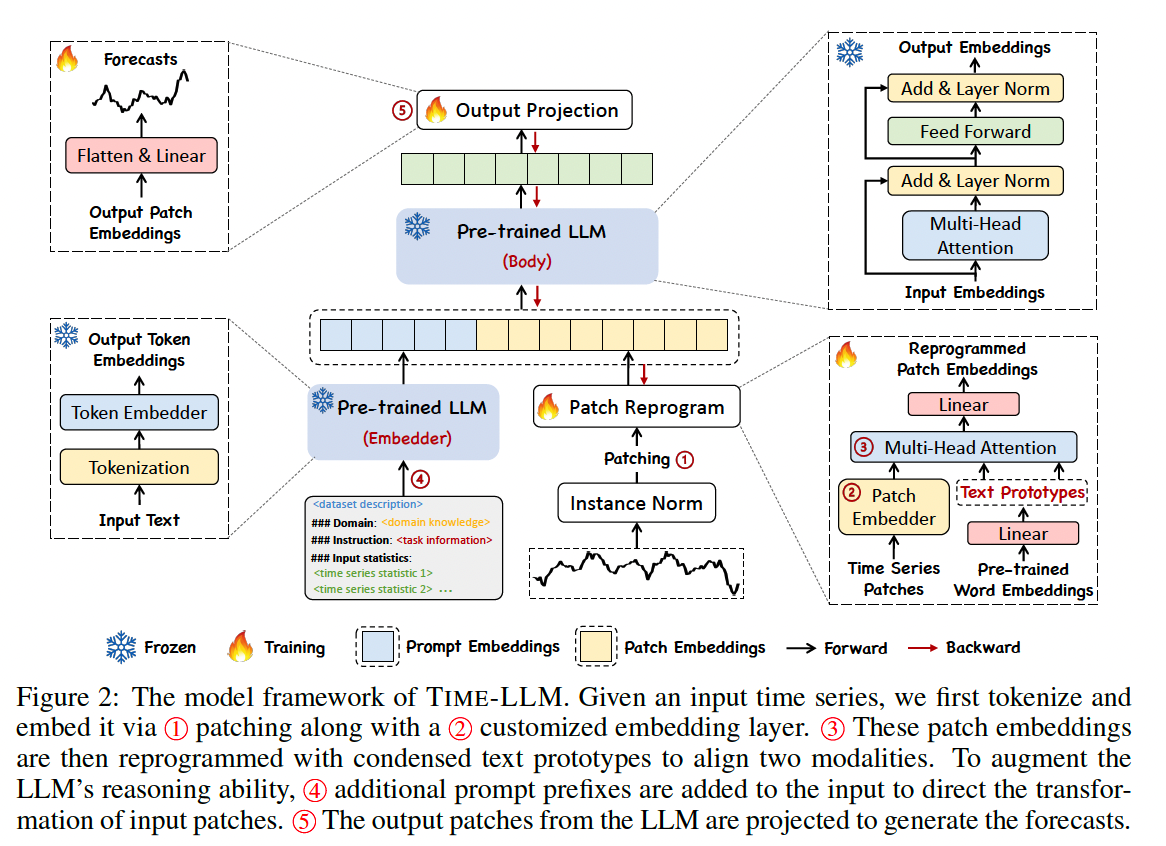
Three main components

• (1) input transformation
• (2) a pre-trained and frozen LLM
• (3) output projection

(Channel Independence) MTS is partitioned into \(N\) UTS! …. \(\mathbf{X}^{(i)} \in \mathbb{R}^{1 \times T}\)

Procedure

• Step 1) Normalization, patching, and embedding ( before being reprogrammed )
• Step 2) Augment the LLM’s TS reasoning ability
  • by prompting it together with reprogrammed patches to generate output representations,
• Step 3) Projected to the final forecasts \(\hat{\mathbf{Y}}^{(i)} \in \mathbb{R}^{1 \times H}\).

Efficiency

• Only the parameters of the lightweight input transformation and output projection are updated

• Directly optimized
  • available with only a small set of TS and a few training epochs
• To further reduce memory footprints, various off-the-shelf techniques (e.g., quantization) can be seamlessly integrated

(1) Model Structure

a) Input Embedding

Unit: each input channel \(\mathbf{X}^{(i)}\)

Procedure

• Step 1) RevIN
• Step 2) Patching ( overlapped or non-overlapped ) with length \(L_p\)
  • Total number of input patches: \(P=\left\lfloor\frac{\left(T-L_p\right)}{S}\right\rfloor+2\),
  • Underlying motivations
    • (1) Better preserving local semantic information by aggregating local information into each patch
    • (2) Serving as tokenization to form a compact sequence of input tokens, reducing computational burdens.
• Step 3) Embeddding ( with simple linear layer )
  • With \(\mathbf{X}_P^{(i)} \in \mathbb{R}^{P \times L_p}\), we embed them as \(\hat{\mathbf{X}}_P^{(i)} \in \mathbb{R}^{P \times d_m}\),

b) Patch Reprogramming

Goal: To align the modalities of TS and natural language to activate the backbone’s TS understanding and reasoning capabilities.

How?

• Reprogram \(\hat{\mathbf{X}}_P^{(i)}\) using pre-trained word embeddings \(\mathbf{E} \in \mathbb{R}^{V \times D}\) in the backbone
• But, no prior knowledge indicating which source tokens are directly relevant!

Simple solution:

• Maintain a small collection of text prototypes by linearly probing \(\mathbf{E}\), denoted as \(\mathbf{E}^{\prime} \in \mathbb{R}^{V^{\prime} \times D}\), where \(V^{\prime} \ll V\).

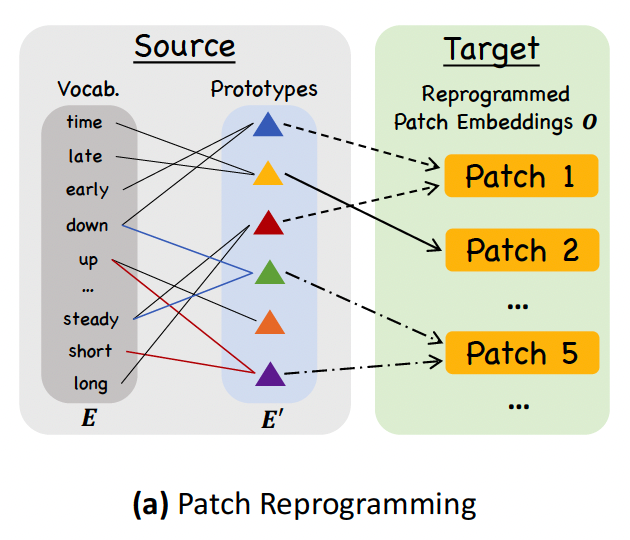
• Efficient & allows for the adaptive selection of relevant source information

• Employ a multi-head cross-attention layer

• Operation to reprogram TS patches in each attention head defined as:

  • \(\mathbf{Z}_k^{(i)}=\operatorname{ATTENTION}\left(\mathbf{Q}_k^{(i)}, \mathbf{K}_k^{(i)}, \mathbf{V}_k^{(i)}\right)=\operatorname{SOFTMAX}\left(\frac{\mathbf{Q}_k^{(i)} \mathbf{K}_k^{(i) \top}}{\sqrt{d_k}}\right) \mathbf{V}_k^{(i)}\).

• Aggregate each \(\mathbf{Z}_k^{(i)} \in \mathbb{R}^{P \times d}\) in every head

  \(\rightarrow\) Obtain \(\mathbf{Z}^{(i)} \in \mathbb{R}^{P \times d_m}\).

  \(\rightarrow\) Linearly projected to align the hidden dimensions with the backbone model: \(\mathbf{O}^{(i)} \in \mathbb{R}^{P \times D}\).

c) Prompt-as-Prefix

Prompting

• Straightforward & effective approach task-specific activation of LLMs
• Problem) Direct translation of TS into natural language ???
• Recent works) Other data modalities can be seamlessly integrated as the prefixes of prompts,
  • Facilitating effective reasoning based on these inputs

Alternative question:

• Can prompts act as prefixes to enrich the input context and guide the transformation of reprogrammed TS patches?

  \(\rightarrow\) Prompt-as-Prefix (PaP)

Prompt-as-Prefix (PaP)

• Significantly enhances the LLM’s adaptability to downstream tasks
• while complementing patch reprogramming

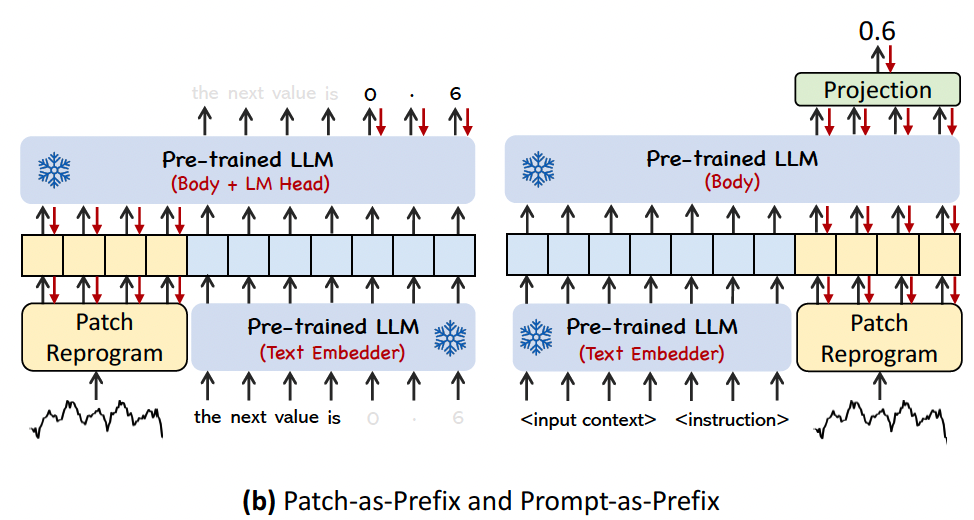
Patch-as-Prefix,

Predict subsequent values in a TS, articulated in natural language

Constraints:

• (1) LLM typically exhibit reduced sensitivity in processing high-precision numerals without the aid of external tools

  \(\rightarrow\) Challenges in accurately addressing practical forecasting tasks over long horizons

• (2) Intricate, customized post-processing is required for different language models

  • Forecasts being represented in disparate natural language formats
    • ex) [’ 0 ‘, ‘, ‘, 6 ‘, ‘ 1 ‘] and [’ 0 ‘, ‘, ‘, ‘61’], to denote the decimal 0.61

Prompt-as-Prefix,

Tactfully avoids these constraints!!!

Identify 3 pivotal components for constructing effective prompts:

• (1) Dataset context
• (2) Task instruction
• (3) Input statistics.

• (1) Dataset context
  • Furnishes the LLM with essential background information concerning the input TS
    • Exhibits distinct characteristics across various domains
• (2) Task instruction
  • Serves as a crucial guide for the LLM in the transformation of patch embeddings for specific tasks.
• (3) Input statistics.
  • Enrich the input TS with additional crucial statistics
    • ex) trends and lags

d) Output Projection.

Discard the prefixal part and obtain the output representations.

Flatten & linear project them: \(\hat{\mathbf{Y}}^{(i)}\).

4. Experiments

Refer to the paper!