On the Importance of Noise Scheduling for Diffusion Models

On the Importance of Noise Scheduling for Diffusion Models

Contents

1. Abstract
2. Why is noise scheduling important for diffusion models?
3. Strategies to adjust noise scheduling
   1. Strategy 1: changing noise schedule functions
   2. Strategy 2: adjusting input scaling factor
   3. Putting it together: a simple compound noise scheduling strategy

0. Abstract

Effect of noise scheduling strategies for diffusion models

Three findings

• (1) Noise scheduling is crucial for the performance
  • Optimal one depends on the task (e.g., image sizes)
• (2) When increasing the image size, the optimal noise scheduling shifts towards a noisier one
  • \(\because\) Increased redundancy in pixels
• (3) Simply scaling the input data by a factor of \(b\) is a good strategy across image sizes.

1. Why is noise scheduling important for diffusion models?

Noising process of data

\(\boldsymbol{x}_t=\sqrt{\gamma(t)} \boldsymbol{x}_0+\sqrt{1-\gamma(t)} \boldsymbol{\epsilon}\).

• \(\boldsymbol{x}_0\) : input example
• \(\boldsymbol{\epsilon}\) : sample from a isotropic Gaussian distributio
• \(t\) : continuous number between 0 and 1 .

Training of diffusion models

• Step 1) Sample \(t \in \mathcal{U}(0,1)\)
• Step 2) Diffuse the input example \(\boldsymbol{x}_0\) to \(\boldsymbol{x}_t\)
• Step 3) Train a denoising network \(f\left(\boldsymbol{x}_t\right)\) to predict
  • either noise \(\boldsymbol{\epsilon}\)
  • or clean data \(\boldsymbol{x}_0\).

\(\rightarrow\) Noise schedule \(\gamma(t)\) determines the distribution of noise levels

Importance of noise schedule

• As we increase the image size, the denoising task at the same noise level (i.e. the same \(\gamma\) ) becomes simpler

• Reason:

  • (1) Redundancy of information in data typically increases with the image size

  • (2) Noises are independently added to each pixels

    \(\rightarrow\) Making it easier to recover the original signal when image size increases

\(\rightarrow\) Optimal schedule at a smaller resolution may not be optimal at a higher resolution

2. Strategies to adjust noise scheduling

Two different noise scheduling strategies

(1) Strategy 1: changing noise schedule functions

Parameterized noise schedule

• based on part of cosine or sigmoid functions + with temperature scaling

Noise schedules

a) Original Cosine schedule [13]

• Fixed part of cosine curve that cannot be adjusted

b) Sigmoid schedule [10]

c) This paper: \(\gamma(t)=1-t\)

• propose a simple linear noise schedule function
  • not the linear schedule proposed in [7]

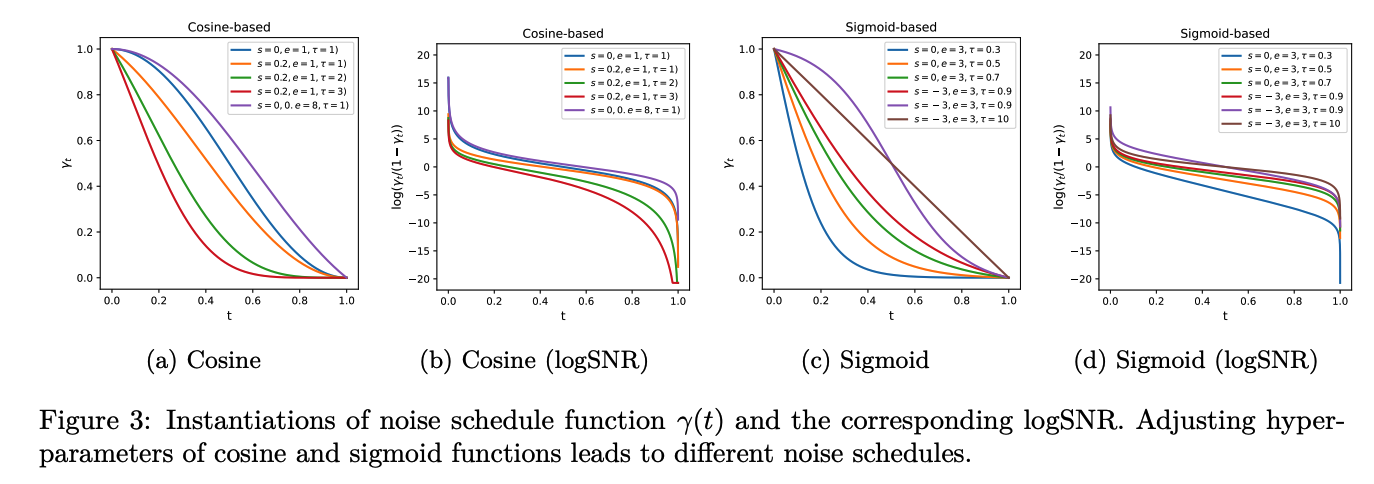
• noise schedule functions under different choice of hyper-parameters

  & corresponding logSNR (signal-to-noise ratio)

• Both cosine and sigmoid functions can parameterize a rich set of noise distributions

  \(\rightarrow\) Choose the hyper-parameters so that the noise distribution is skewed towards noisier levels

(2) Strategy 2: adjusting input scaling factor

Indirectly adjust noise scheduling

\(\rightarrow\) scale the input \(\boldsymbol{x}_0\) by a constant factor \(b\),

• \(\boldsymbol{x}_t=\sqrt{\gamma(t)} b \boldsymbol{x}_0+\sqrt{1-\gamma(t)} \boldsymbol{\epsilon}\).

• As we reduce the scaling factor \(b\), it increases the noise levels

When \(b \neq 1\) …

\(\rightarrow\) Variance of \(\boldsymbol{x}_t\) can change …. could lead to decreased performance

\(\rightarrow\) To ensure the variance keep fixed, scale \(\boldsymbol{x}_t\) by a factor of \(\frac{1}{\left(b^2-1\right) \gamma(t)+1}\).

• However, in practice, we find that it works well by simply normalize the \(\boldsymbol{x}_t\) by its variance to make sure it has unit variance before feeding it to the denoising network \(f(\cdot)\).

  = Variance normalization operation

  = Can be seen as the first layer of the denoising network

Similar to changing the noise scheduling function \(\gamma(t)\) ….

But achieves slightly different effect in the logSNR when compared to cosine and sigmoid schedules, particularly when \(t\) is closer to 0 [ Figure 5 ]

Input scaling = shifts the logSNR along y-axis while keeping its shape unchanged

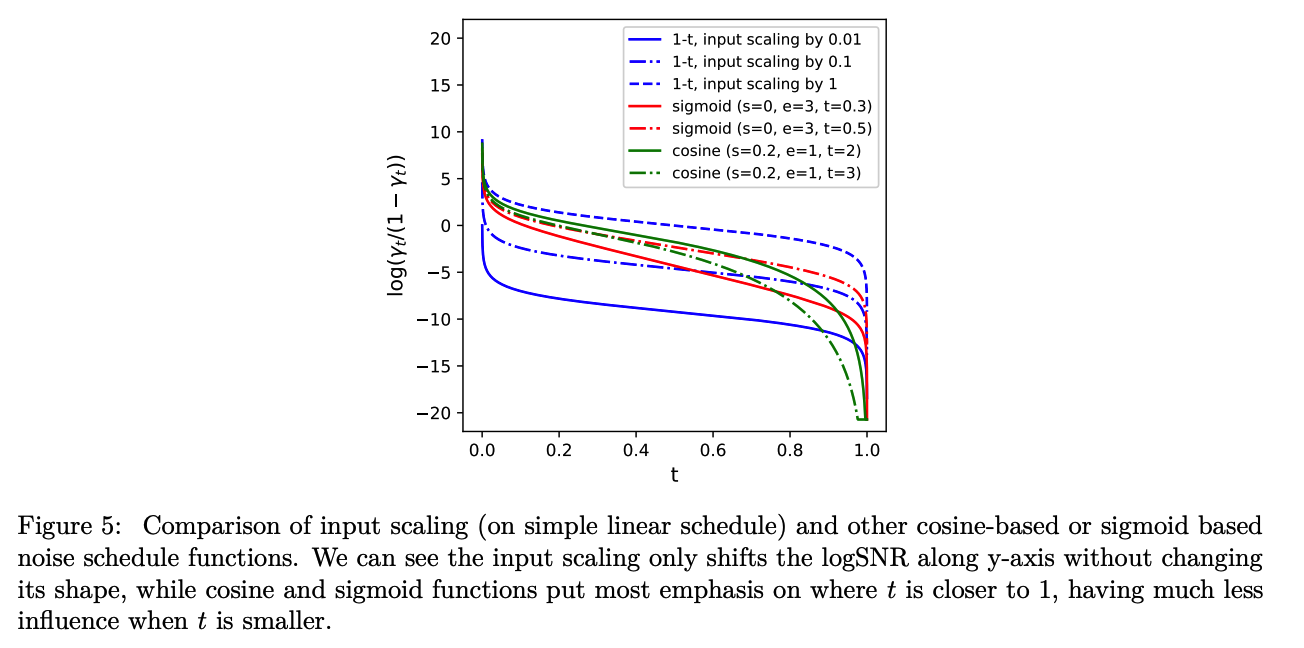
(3) Putting it together: a simple compound noise scheduling strategy

Propose to combine these two strategies

• by having a single noise schedule function, such as \(\gamma(t)=1-t\), & **scale the input by a factor of \(b\). **