Transformer-Modulated Diffusion Models for Probabilistic MTS Forecasting

Transformer-Modulated Diffusion Models for Probabilistic MTS Forecasting

Contents

1. Abstract
2. Introduction
3. Diffusion model in TS
4. TMDM
   1. Learning Transformer powered conditions
   2. Conditional Diffusion-based TS Generative Model

Abstract

Transformer: neglect uncertainty in predicted TS

TMDM (Transformer-Modulated Diffusion Model)

• Harness the power of transformer
  • Utilize the information from transformer as prior
  • Capture covariate-dependence in both forward & reverse
• Introduce 2 novel metrics for uncertainty estimation

1. Introduction

Uncertainty estimation

= capture the uncertainty of \(\boldsymbol{y}_{0: M}\) given \(\boldsymbol{x}_{0: N}\).

Transformer-Modulated Diffusion Model (TMDM)

Unifies the conditional diffusion generative process with transformers

Primary objective:

• Recover the full distn of future TS \(\boldsymbol{y}_{0: M}\),
• Conditioned on the representation captured by existing transformer-based method

2. Diffusion model in TS

Conditional embedding is fed into the denoising network

• TimeGrad: hidden state from RNN
• TimeDiff: embedding based on two features explicitly designed for TS
• TMDM: employs conditional information as a prior knowledge for both forward & reverse process

Contributions

1. TMDM, a transformer-based diffusion generative framework
2. Integrates diffusion & transformer-based models within a cohesive Bayesian framework
3. Explore the application of PICP & QICE as metrics in probabilistic MTS forecasting for uncertainty estimation

3. TMDM

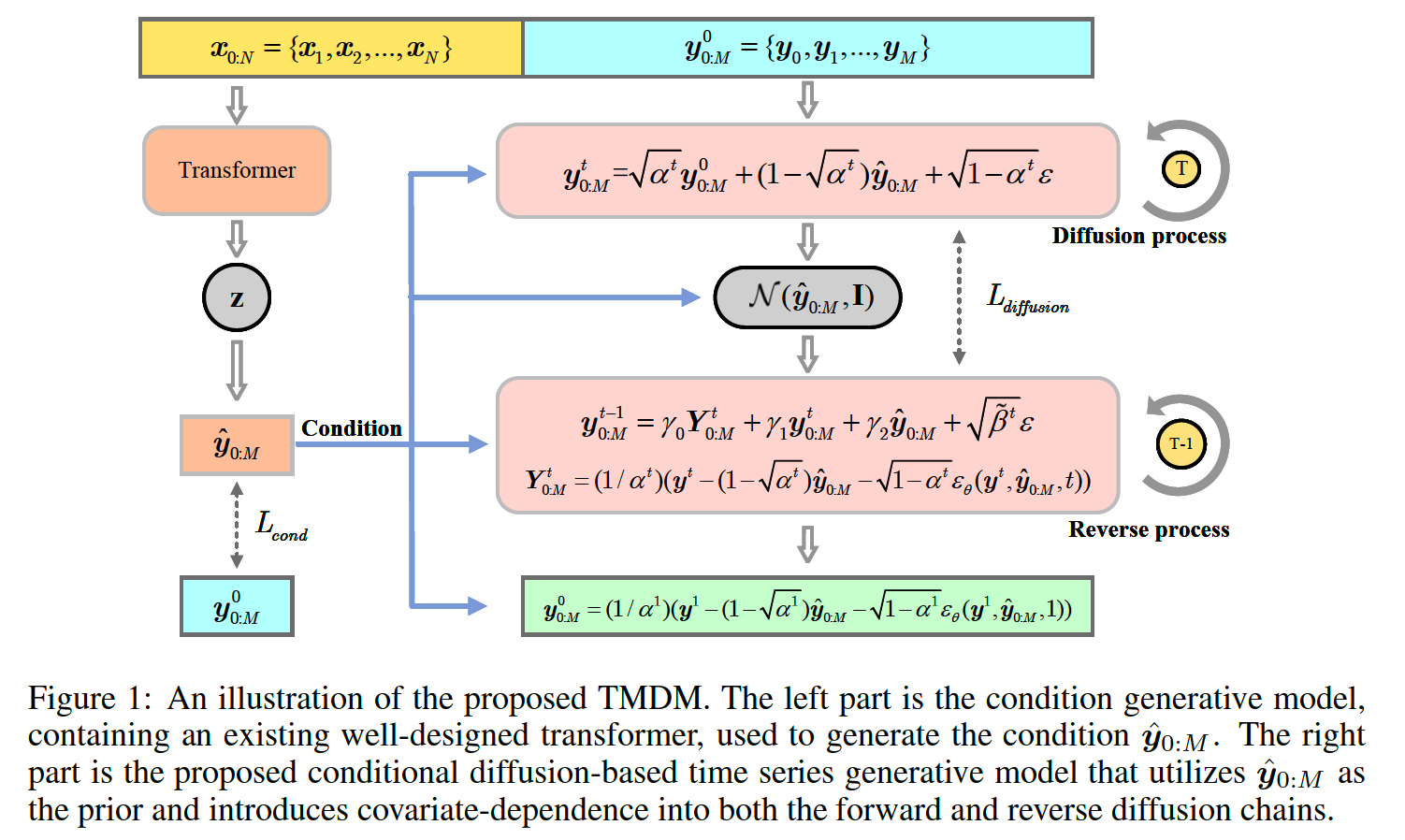
Transformer models

• excel at accurately estimating the conditional mean \(\left.\mathbb{E} \mid \boldsymbol{y}_{0: M} \mid \boldsymbol{x}_{0: N}\right]\)

TMDM

• extends this capability to recover the full distribution of the future time series \(\boldsymbol{y}_{0: M}\).

2 main components

1. Transformer-powered conditional distribution learning model (condition generative model)
2. Conditional diffusion-based time series generative model

\(\rightarrow\) Integrated into a unified Bayesian framework, leveraging a hybrid optimization approach

\(p\left(\boldsymbol{y}_{0: M}^0\right)=\int_{\boldsymbol{y}_{0: M}^{1: T}} \int_{\boldsymbol{z}} p\left(\boldsymbol{y}_{0: M}^T \mid \hat{\boldsymbol{y}}_{0: M}\right) \prod_{t=1}^T p\left(\boldsymbol{y}_{0: M}^{t-1} \mid \boldsymbol{y}_{0: M}^t, \hat{\boldsymbol{y}}_{0: M}\right) p\left(\hat{\boldsymbol{y}}_{0: M} \mid \boldsymbol{z}\right) p(\boldsymbol{z}) d \boldsymbol{z} d \boldsymbol{y}_{0: M}^{1: T}\).

• historical time series \(\boldsymbol{x}_{0: M}\)
• model a latent variable \(\boldsymbol{z}\) using transformer
• generates a conditional representation \(\hat{\boldsymbol{y}}_{0: M}\) with \(\boldsymbol{z}\)
  • \(\rightarrow\) us this as a condition for forward and reverse processes

(1) Learning Transformer powered conditions

\(q\left(\boldsymbol{z} \mid \mathscr{T}\left(\boldsymbol{x}_{0: N}\right)\right) \sim \mathcal{N}\left(\tilde{\boldsymbol{\mu}}_z\left(\mathscr{T}\left(\boldsymbol{x}_{0: N}\right)\right), \tilde{\boldsymbol{\sigma}}_z\left(\mathscr{T}\left(\boldsymbol{x}_{0: N}\right)\right)\right)\).

• Transformer structure \(\mathscr{T}(\cdot)\)
• Historical time series \(\boldsymbol{x}_{0: N}\)

\(\rightarrow\) Capture the representation by \(\mathscr{T}\left(\boldsymbol{x}_{0: N}\right)\).

\(\rightarrow\) Serves as the guiding factor for approximating the true posterior distribution of \(z\).

Given a well-learned \(\boldsymbol{z}\) ….. generate the conditional representation \(\hat{\boldsymbol{y}}_{0: M}\) :

\(\boldsymbol{z} \sim \mathcal{N}(0,1) \quad \text { and } \quad \hat{\boldsymbol{y}}_{0: M} \sim \mathcal{N}\left(\boldsymbol{\mu}_z(\boldsymbol{z}), \boldsymbol{\sigma}_z\right)\).

\(\rightarrow\) Used in forward and reverse processes in TMDM.

(2) Conditional Diffusion-based TS Generative Model

Incorporate the conditional representation \(\hat{\boldsymbol{y}}_{0: M}\) into \(p\left(\boldsymbol{y}_{0: M}^T\right)\)

• can be viewed as prior knowledge for estimating the conditional mean \(\mathbb{E}\left[\boldsymbol{y}_{0: M} \mid \boldsymbol{x}_{0: N}\right]\)

a) Forward

Conditional distributions for the forward process

• \(q\left(\boldsymbol{y}_{0: M}^t \mid \boldsymbol{y}_{0: M}^{t-1}, \hat{\boldsymbol{y}}_{0: M}\right) \sim \mathcal{N}\left(\boldsymbol{y}_{0: M}^t \mid \sqrt{1-\beta^t} \boldsymbol{y}_{0: M}^{t-1}+\left(1-\sqrt{1-\beta^t}\right) \hat{\boldsymbol{y}}_{0: M}, \beta^t \boldsymbol{I}\right)\).

b) Backward

• \(q\left(\boldsymbol{y}_{0: M}^{t-1} \mid \boldsymbol{y}_{0: M}^0, \boldsymbol{y}_{0: M}^t, \hat{\boldsymbol{y}}_{0: M}\right) \sim \mathcal{N}\left(\boldsymbol{y}_{0: M}^{t-1} \mid \gamma_0 \boldsymbol{y}_{0: M}^0+\gamma_1 \boldsymbol{y}_{0: M}^t+\gamma_2 \hat{\boldsymbol{y}}_{0: M}, \tilde{\beta}^t \boldsymbol{I}\right)\).
  • \(\gamma_0=\frac{\beta^t \sqrt{\alpha^{t-1}}}{1-\alpha^t}, \gamma_1=\frac{\left(1-\alpha^{t-1}\right) \sqrt{\bar{\alpha}^t}}{1-\alpha^t}, \gamma_2=1+\frac{\left(\sqrt{\alpha^t}-1\right)\left(\sqrt{\bar{\alpha}^t}+\sqrt{\alpha^{t-1}}\right)}{1-\alpha^t}, \tilde{\beta}^t=\frac{\left(1-\alpha^{t-1}\right)}{1-\alpha^t} \beta^t\).