(paper) Multivariate Time Series Regression with Graph Neural Networks

Multivariate Time Series Regression with Graph Neural Networks (20202)

Contents

1. Abstract
2. Introduction
3. Related Works
   1. Deep Learning on Graphs
   2. GNN
   3. GNN for Time Series Analysis
   4. Deep Learning for Seismic Analysis
4. Method
   1. Basic Model Architecture
   2. Model Implementation
      1. CNN for Feature Extraction
      2. GNN Processing
   3. Model Training

0. Abstract

Spatial-Temporal GNNs for TS forecasting

• (1) spatial info can be exploited by graph structures,

• along with (2) sequential info

1. Introduction

combine the capabilities of ..

• (1) CNN (feature extraction)
• (2) GNN (spatial information)

test our proposed models on network-based seismic data

2. Related Works

(1) Deep Learning on Graphs

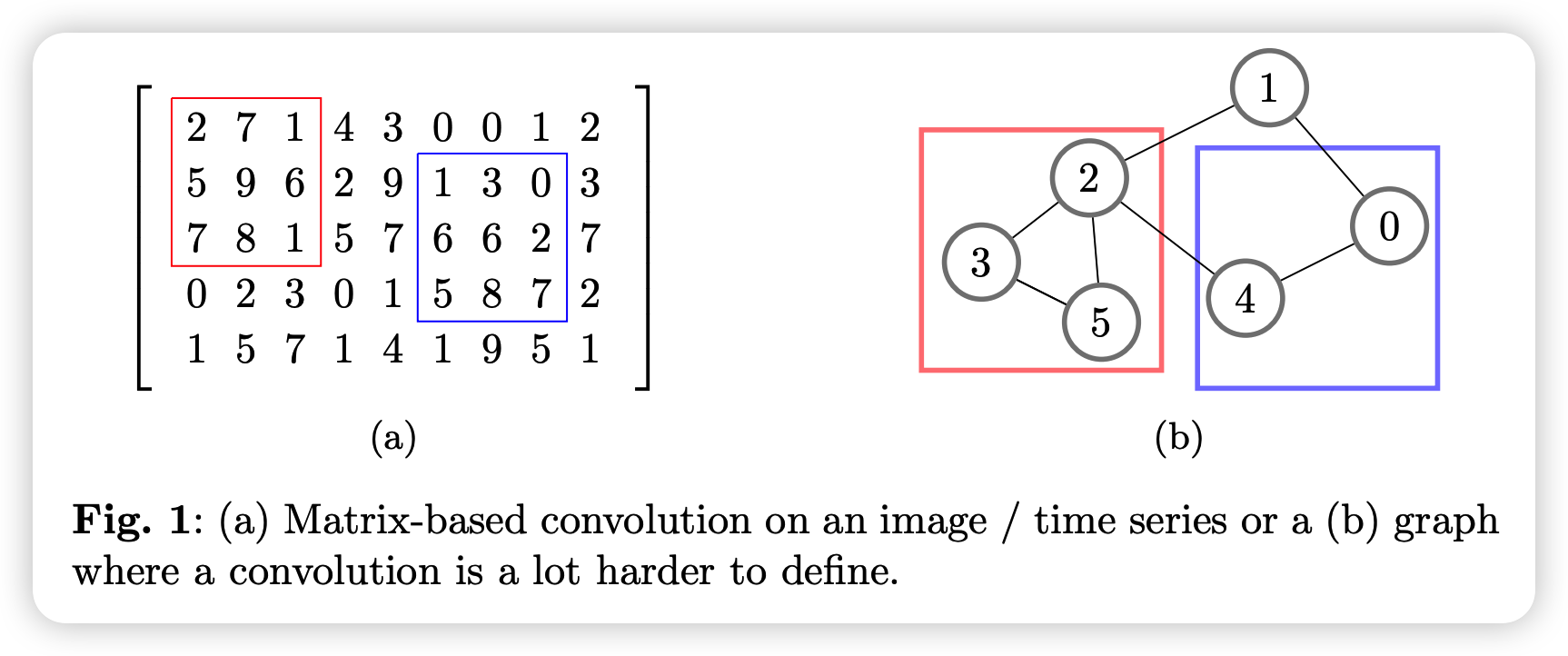
standard CNN convolutions are not applicable to graph-structed data, due to non-euclidean nature

(2) GNN

there are 2 main classes of methods that GNN us

• (1) spectral methods
• (2) spatial methods

Spectral methods

• use eigenvectors and eigenvalues of a matrix, with eigendecomposition
• perform convolutions with the
  • Graph Fourier Transformation
  • inverse Graph Fourier Transformation

Spatial methods

• use message passing
  • look at local neighborhood of nodes
  • perform calculations on their top-k neighbors
• node aggregation/update function \(f\)
  • node representation : \(Z = f(G)X\)
    • \(G\) : adjacency/Laplacian matrix
    • \(X\) : node features in \(G\)

Spatial methods :

• focus more on connectivity

Spectral methods :

• focuson eigenvalues & eigenvectors of a graph

GCN ( Graph Convolutional Networks )

propoagation rule :

• \(H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right)\).

Notation

• \(H^{(l)} \in \mathbb{R}^{N \times D}\) : matrix of activations of the \(l\) th layer,

• \(\tilde{D}=\sum_{j} \tilde{A}_{i j}\) : dgree matrix

• \(\tilde{A}=A+I_{N}\) : adjacency matrix of the undirected graph \(G\)

  ( with the added self-connections \(I_{N}\) )

(3) GNN for Time Series Analysis

most of proposed models combine GNN + RNN

• focus on modeling long-term dependencies

However, when the task is classification / regression ….

\(\rightarrow\) there is a lack of long-term dependecies

(4) Deep Learning for Seismic Analysis

for waveform analysis…CNN has been applied

3. Method

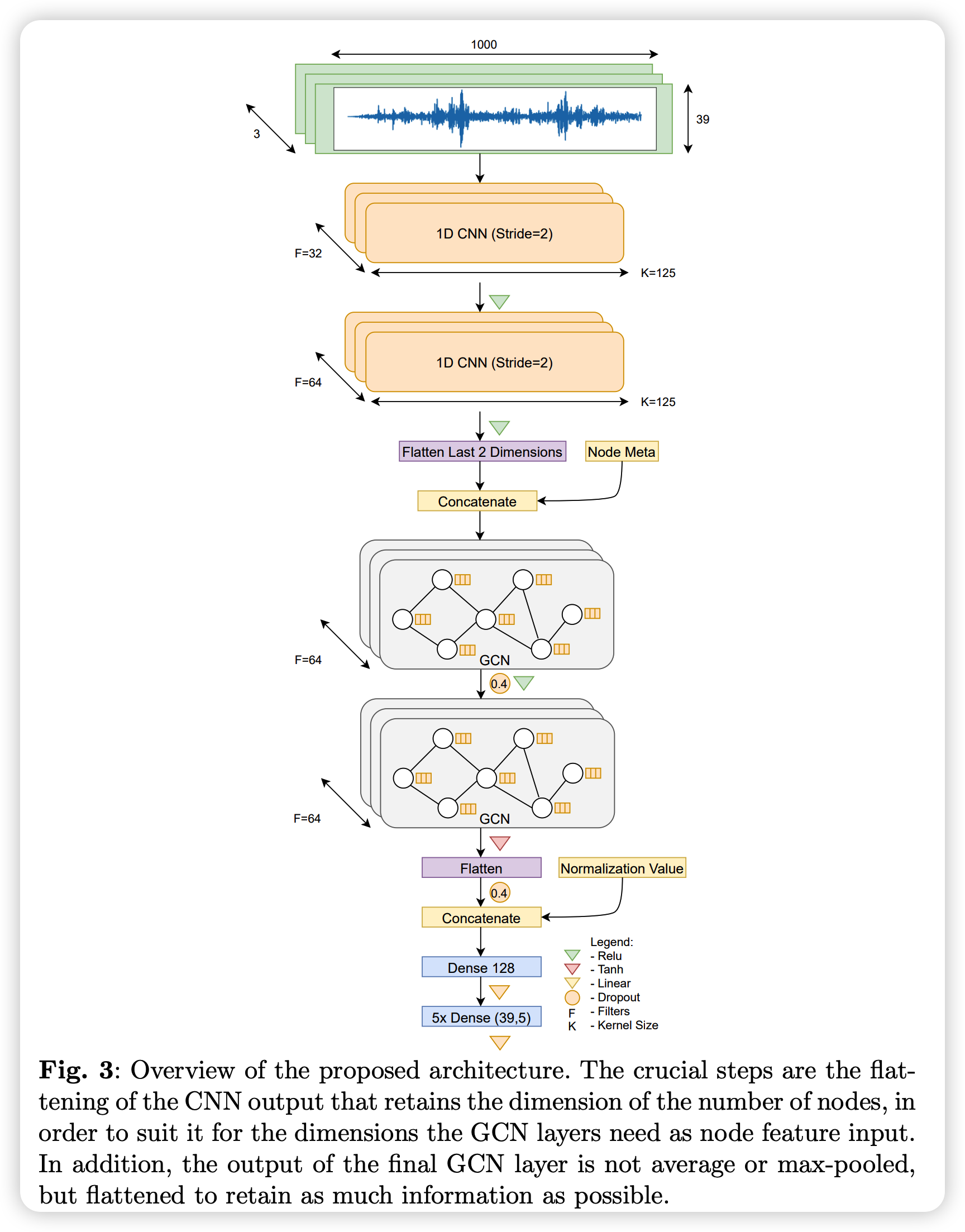
(1) Basic Model Architecture

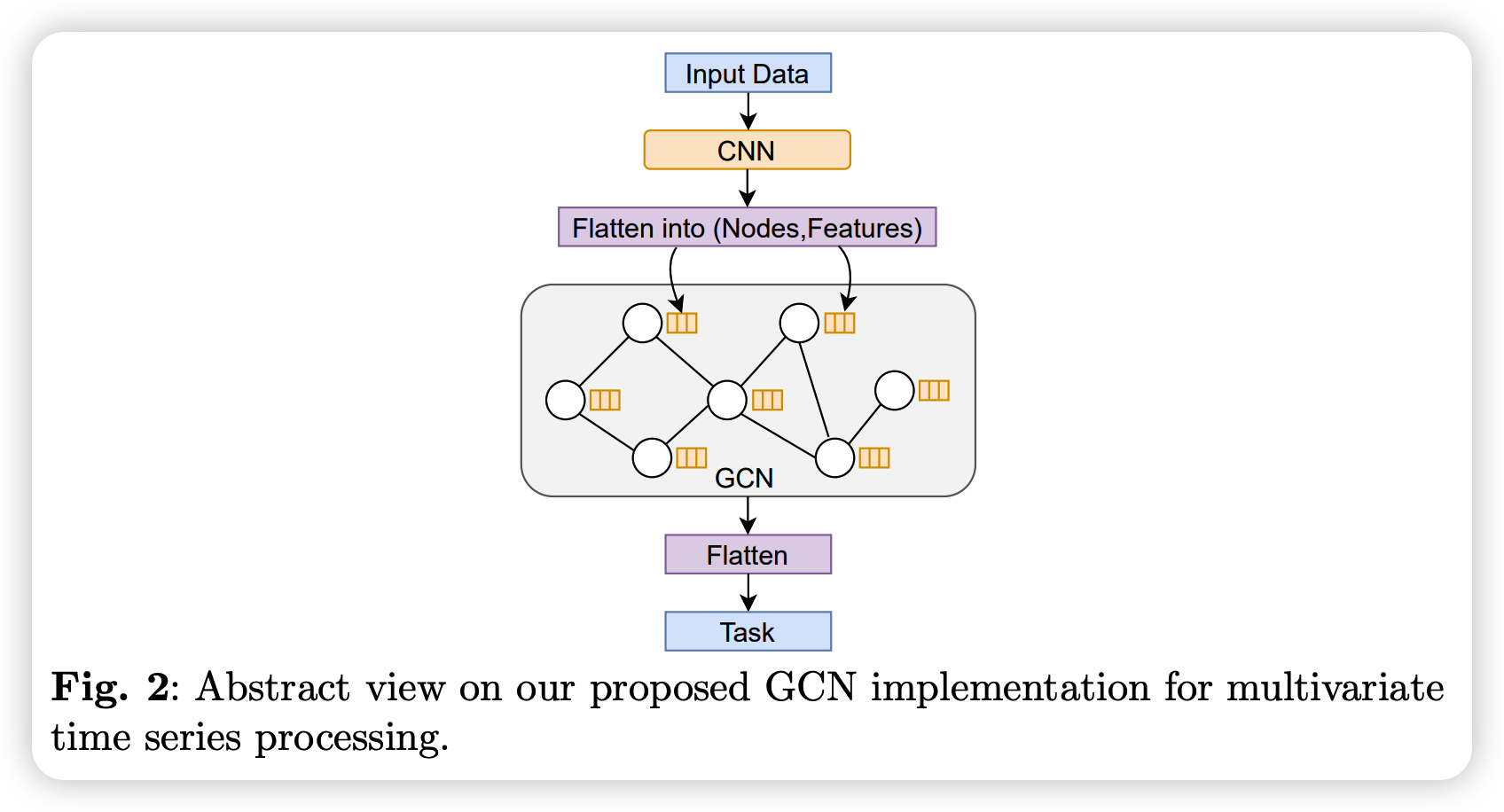
3 key points

• (1) to obtain node features..
  • use 1D-CNN
• (2) GNN of \(n\) layers
  • for processing these feature vectors
• (3) flatten entire GCN feature output
  • put on dense layer for desired task
  • average/max pooling (X)

(2) Model Implementation

CNN for Feature Extraction

1D-conv

• second block ( in the pciture above )

• TWO 1d-cnn layers : act as feature extractors

• purpose : learn temporal patterns

• last 2 dimensions of the second CNN are flattened

  \(\rightarrow\) make the dimension fitted for GNN layers ( input : (\(N,F\) ) )

• Notation

  • \(N\) : number of nodes
  • \(F\) : 1-d vector of node feature \([x_1, … x_n]\)

GNN Processing

next layer: GNN layers ( which uses GCN )

(3) Model Training