Lag-Llama: Towards Foundation Models for Time Series Forecasting
Contents
- Abstract
- Introduction
- Probabilistic TS Forecasting
- Lag-Llama
- Experiments
Abstract
Lag-Llama
- General-purpose univariate probabilistic TS forecasting model
- Trained on a large collection of TS data.
- Good zero-shot prediction capabilities on unseen “out-of-distribution” TS datasets
- Use smoothly broken power-laws to fit and predict model scaling behavior
( Code: https://github.com/kashif/pytorch-transformer-ts )
1. Introduction
Train a transformer model on a large collection of TS datasets and evaluate its performance on an unseen “out-of-distribution” dataset
( large collection of time series from the Monash Time Series Repository )
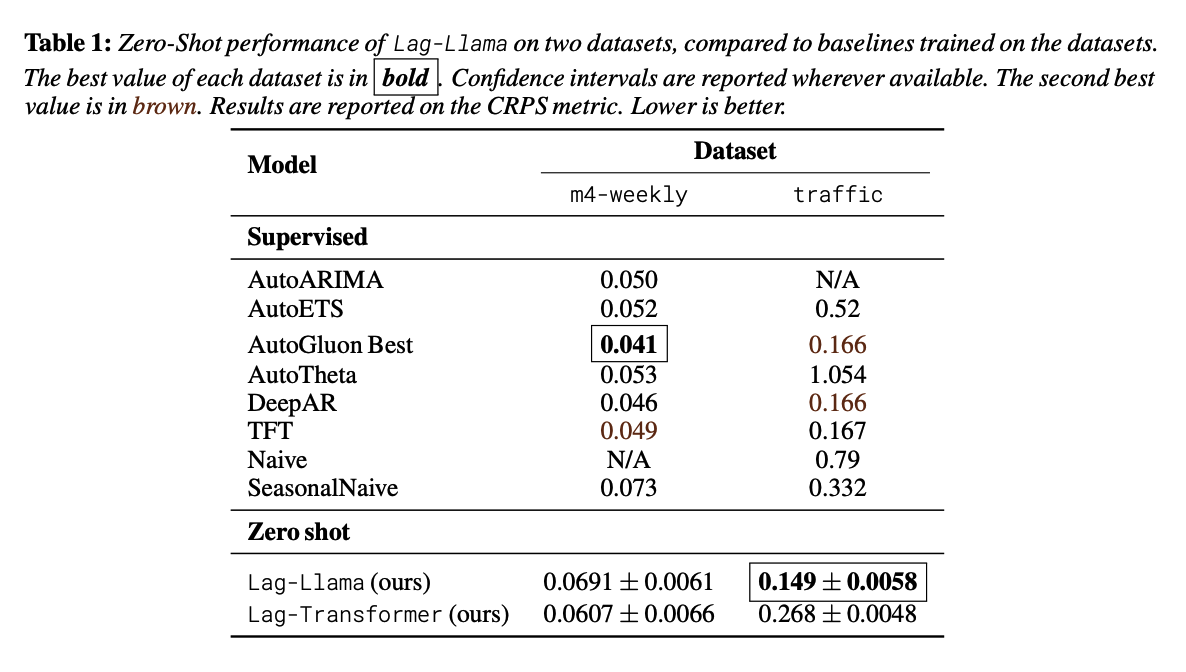
Experiments
- Test-set performance of this model on unseen time-series datasets
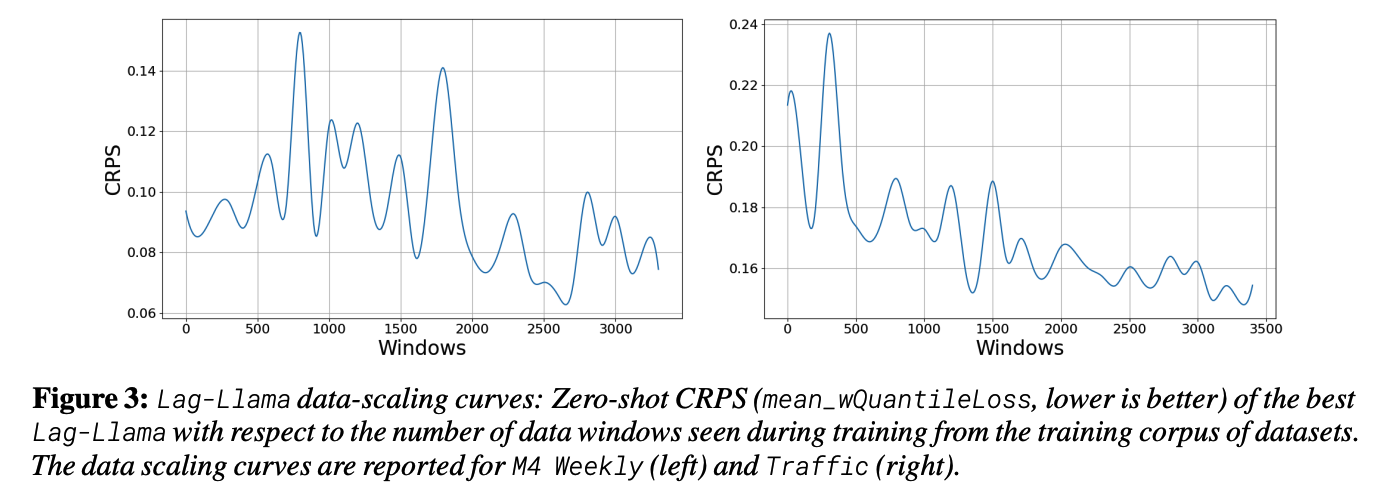
- Present a neural scaling laws study on the number of parameters and training data.
Contributions
-
Propose Lag-Llama
- a model for univariate probabilistic time-series forecasting
- suitable for scaling law analyses of TS foundation models
-
Train Lag-Llama on a corpus of TS datasets
Test zero-shot on unseen time series datasets
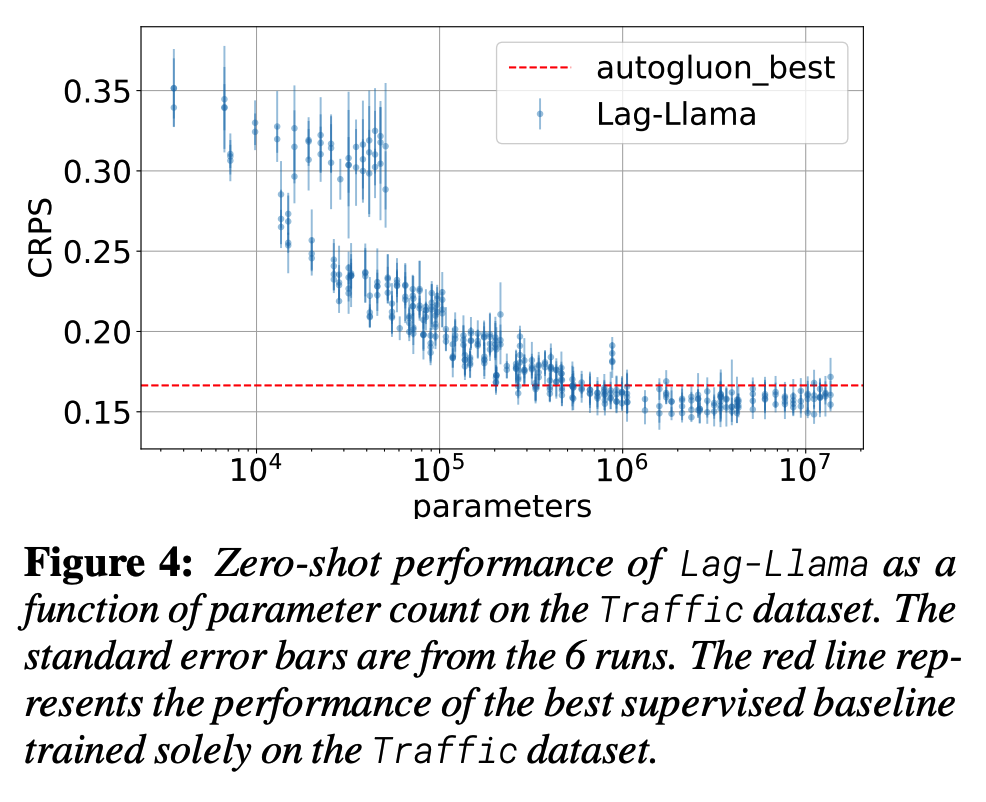
Identify a “stable” regime where the model constantly outperforms the baselines beyond a certain model size
-
Fit empirical scaling laws of the zero-shot test performance of the model as a function of the model size
\(\rightarrow\) allowing us to potentially extrapolate and predict generalization beyond the models used in this paper.
2. Probabilistic TS Forecasting
Notation
- \(\mathcal{D}_{\text {train }}=\left\{x_{1: T^i}^i\right\}_{i=1}^D\),
- at each time point \(t \in\left\{1, \ldots, T^i\right\}, x_t^i \in \mathbb{R}\)
- Goal: predict \(P \geq 1\) steps into the future
- \(\mathcal{D}_{\text {test }}=\left\{x_{T^i+1: T^i+P}\right\}_{i=1}^D\) or some held-out TS dataset
- Covariates \(\mathbf{c}_t^i\)
- assumed to be non-stochastic and available in advance for the \(P\) future time points.
Univariate probabilistic time series forecasting
- \(p_{\mathcal{X}}\left(x_{t+1: t+P}^i \mid x_{1: t}^i, \mathbf{c}_{1: t+P}^i\right)\).
Sub-sample fixed context windows of size \(C \geq 1\)
- \(p_{\mathcal{X}}\left(x_{C+1: C+P}^i \mid x_{1: C}^i, \mathbf{c}_{1: C-1+P}^i\right)\).
Autoregressive model
- \(p_{\mathcal{X}}\left(x_{C+1: C+P}^i \mid x_{1: C}^i, \mathbf{c}_{1: C-1+P}^i ; \theta\right)=\prod_{t=C+1}^{C+P} p_{\mathcal{X}}\left(x_t^i \mid x_{1: t-1}^i, \mathbf{c}_{1: t-1}^i ; \theta\right)\).
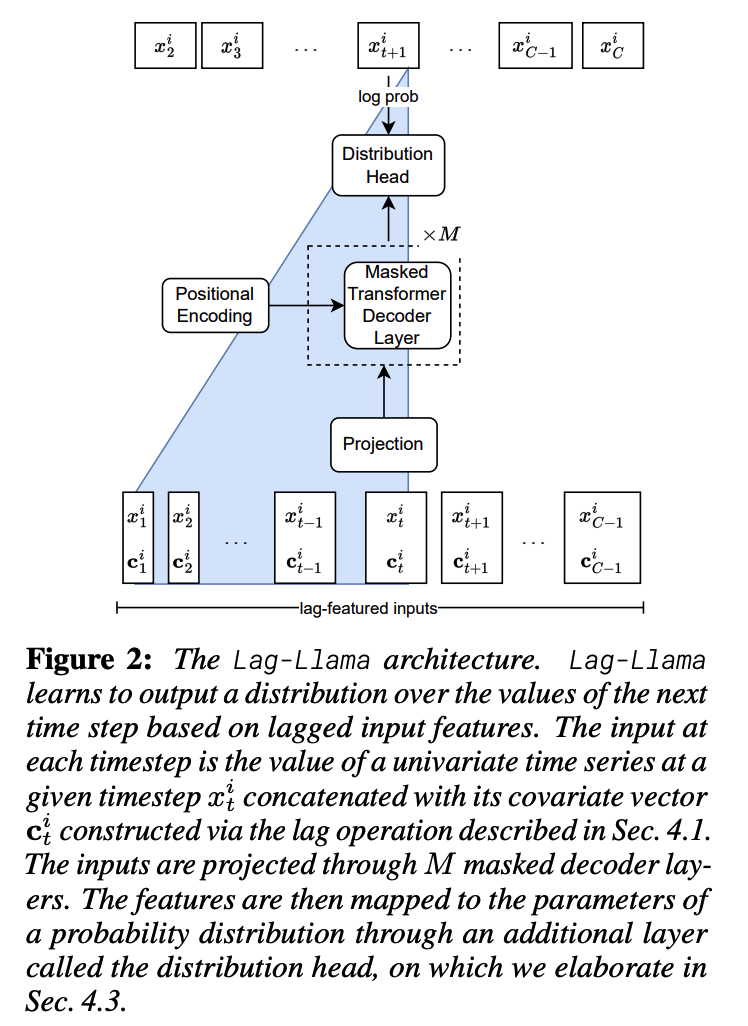
3. Lag-Llama
(1) Lag Features
The only covariates we employ in this model are from the target values, in particular lag features
- lags are constructed from a set of appropriate lag indices for quarterly, monthly, weekly, daily, hourly, and second-level frequencies that correspond to the frequencies in our corpus of time series data
Lag
-
Lag indices \(\mathcal{L}=\{1, \ldots, L\}\)
-
Lag operation on a particular time value as \(x_t \mapsto \mathbf{c}_t \in \mathbb{R}^{ \mid \mathcal{L} \mid }\)
- where each entry \(j\) of \(\mathbf{c}_t\) is given by \(\mathbf{c}_t[j]=x_{t-\mathcal{L}[j]}\).
-
Thus to create lag features for some context-length window \(x_{1: C}\) …
\(\rightarrow\) Need to sample a larger window with \(L\) more historical points denoted by \(x_{-L+1: C}\).
Other than lag, use overlapped patches
\(\rightarrow\) resulting in a sequence of vectors whose dimension can be specified
\(\rightarrow\) can lead to vectors whose entries are causally mixed. See Fig. 1 for an example of both approaches
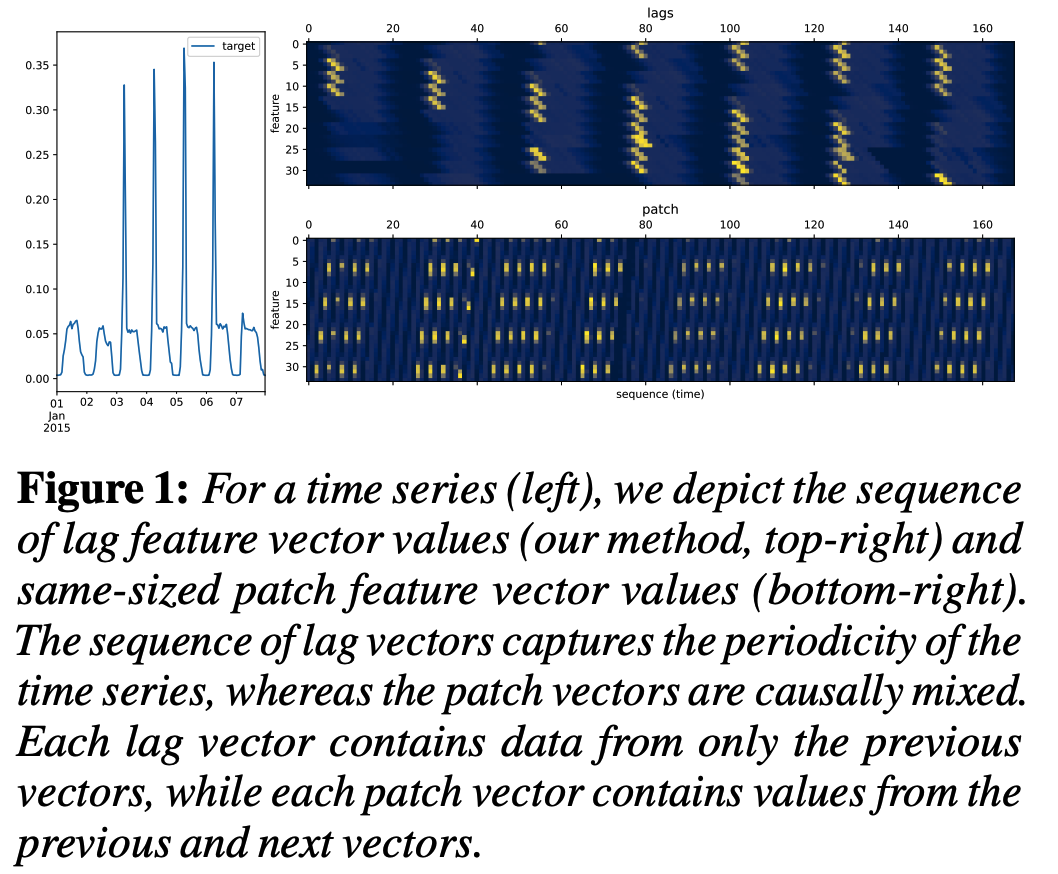
Lag vs. Patch
-
Both approaches essentially serve the same purpose
-
Lag Pos
-
Indices of the lags correspond directly to the various possible seasonalities of the data
\(\rightarrow\) advantage of preserving the date-time index causal structure
-
Can use masked decoders during training and autoregressive sampling at inference time
( which is not trivial with patches. )
-
-
Lag Cons
- Cownside to using lags is that it requires an \(L\)-sized or larger context window at inference time.
(2) Architecture
Based on the recent LlaMA [43] architecture
- incorporates prenormalization via the RMSNorm
- adds Rotary Positional Encoding (RoPE)
- to each attention layer’s query and key representations.
Inference time
-
Construct a feature vector
-
Can obtain many samples from the predicted distribution
& Concatenate them to the initial sequence to obtain further lag vectors
-
( via greedy autoregressive decoding ) Able to obtain many simulated trajectories
\(\rightarrow\) Can calculate the uncertainty intervals for downstream decision-making tasks and metrics with respect to held-out data.
(3) Choice of Distribution Head
Last layer of Lag-Llama = Distribution head
- Projects the model’s features to the parameters of a probability distribution.
- Use Student’s \(t\)-distribution: output the three parameters corresponding to this distribution
- degrees of freedom
- mean
- scale
(4) Value Scaling
Dataset can have any numerical magnitude11
\(\rightarrow\) Utilize the scaling heuristic from [36]
- For each univariate window, we calculate its
- mean value \(\mu^i=\sum_{t=-L}^C x_t^i /(C+L)\)
- variance \(\sigma^i\).
- Time series \(\left\{x_t^i\right\}_{t=-L}^C\) \(\rightarrow\) \(\left\{\left(x_t^i-\mu^i\right) / \sigma^i\right\}_{t=-L}^C\).
- Also incorporate \(\mu^i\) via \(\operatorname{sign}\left(\mu^i\right) \log \left(1+ \mid \mu^i \mid \right)\) as well as \(\log \left(\sigma^i\right)\) as time independent real-valued covariates.
During training and obtaining likelihood…
- the values are transformed using the mean and variance
During sampling…
- every timestep of data that is sampled is de-standardized using the same mean and variance.
(5) Augmentation
Freq-Mix & Freq-Mask
4. Experiments