Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting (2019, 193)
Contents
- Abstract
- Introduction
- Background
- Problem Definition
- Transformer
- Methodology
- Enhancing the locality of Transformer
- Breaking the memory bottleneck of Transformer
0. Abstract
propose to tackle Transformer
2 major weakness
- 1) locality-agnostic
- point-wise dot-production self attention is “insensitive” to local context
- 2) memory bottleneck
- space complexity of Transformer “grows quadratically” with sequence length $L$
Proposal
- propose “CONVOLUTIONAL self-attention”
- by producing Q & K with “causal convolution”
- propose “LogSparse Transformer”
- $O(L(logL)^2)$ memory cost
1. Introduction
Traditional TSF models
- ex) SSMs, AR models $\rightarrow$ fit EACH TS independently & manually select trend/seasonality
Transformer
- leverage attention mechansim
- BUT, canonical dot-product self-attention : insensitive to LOCAL context
- also, BAD space complexity
2. Background
(1) Problem Definition
Univariate Time Series ( # of data : $N$ ) :
- $\left{\mathbf{z}{i, 1: t{0}}\right}_{i=1}^{N}$
- $\mathbf{z}{i, 1: t{0}} \triangleq\left[\mathbf{z}{i, 1}, \mathbf{z}{i, 2}, \cdots, \mathbf{z}{i, t{0}}\right]$ , where $\mathbf{z}_{i, t} \in \mathbb{R}$
Covariate : $\left{\mathrm{x}{i, 1: t{0}+\tau}\right}_{i=1}^{N}$
- known entire period
Goal : predict the next $\tau$ time steps ( $\left{\mathbf{z}{i, t{0}+1: t_{0}+\tau}\right}_{i=1}^{N} $ )
Model : conditional distribution…
$p\left(\mathbf{z}{i, t{0}+1: t_{0}+\tau} \mid \mathbf{z}{i, 1: t{0}}, \mathbf{x}{i, 1: t{0}+\tau} ; \boldsymbol{\Phi}\right)=\prod_{t=t_{0}+1}^{t_{0}+\tau} p\left(\mathbf{z}{i, t} \mid \mathbf{z}{i, 1: t-1}, \mathbf{x}_{i, 1: t} ; \boldsymbol{\Phi}\right)$.
- reduce to “one-step-ahead prediction model”
- use both “observation & covariates”
- $\mathbf{y}{t} \triangleq\left[\mathbf{z}{t-1} \circ \mathbf{x}{t}\right] \in \mathbb{R}^{d+1}, \quad \mathbf{Y}{t}=\left[\mathbf{y}{1}, \cdots, \mathbf{y}{t}\right]^{T} \in \mathbb{R}^{t \times(d+1)}$.
(2) Transformer
capture both LONG & SHORT term dependencies ( with different attention heads )
$\mathbf{O}{h}=\operatorname{Attention}\left(\mathbf{Q}{h}, \mathbf{K}{h}, \mathbf{V}{h}\right)=\operatorname{softmax}\left(\frac{\mathbf{Q}{h} \mathbf{K}{h}^{T}}{\sqrt{d_{k}}} \cdot \mathbf{M}\right) \mathbf{V}_{h}$.
-
$\mathbf{Q}{h}=\mathbf{Y} \mathbf{W}{h}^{Q}$.
-
$\mathbf{K}{h}=\mathbf{Y} \mathbf{W}{h}^{K}$.
-
$\mathbf{V}{h}=\mathbf{Y} \mathbf{W}{h}^{V}$.
with $h=1, \cdots, H .$
-
$\mathbf{M}$ : mask matrix ( setting all upper triangular elements to $-\infty$ )
Parameters
- $\mathbf{W}{h}^{Q}, \mathbf{W}{h}^{K} \in \mathbb{R}^{(d+1) \times d_{k}}$.
- $\mathbf{W}{h}^{V} \in \mathbb{R}^{(d+1) \times d{v}}$.
Afterwards, $\mathbf{O}{1}, \mathbf{O}{2}, \cdots, \mathbf{O}_{H}$ are concatenated & FC layer
3. Methodology
(1) Enhancing the locality of Transformer
Patterns in time series may evolve with time!
Self-attention
- original ) point-wise
- proposed ) convolution
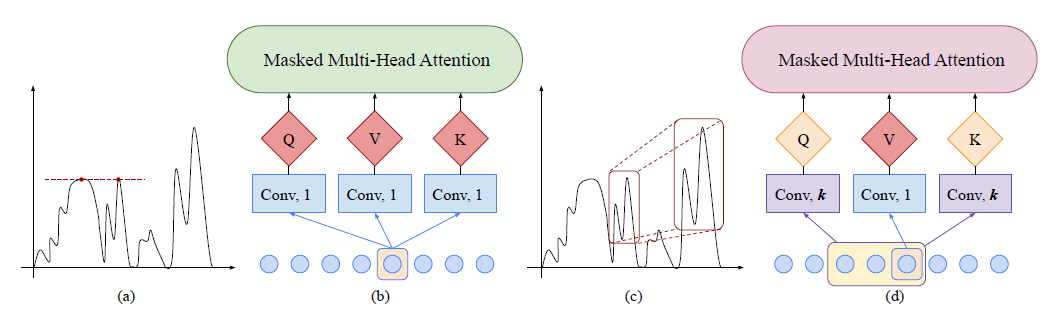
Causal Convolution
-
filter of kernel size $k$ with stride $1$
-
to get Q & K
( V is still produced by point-wise attention )
-
more aware of local context
(2) Breaking the memory bottleneck of Transformer
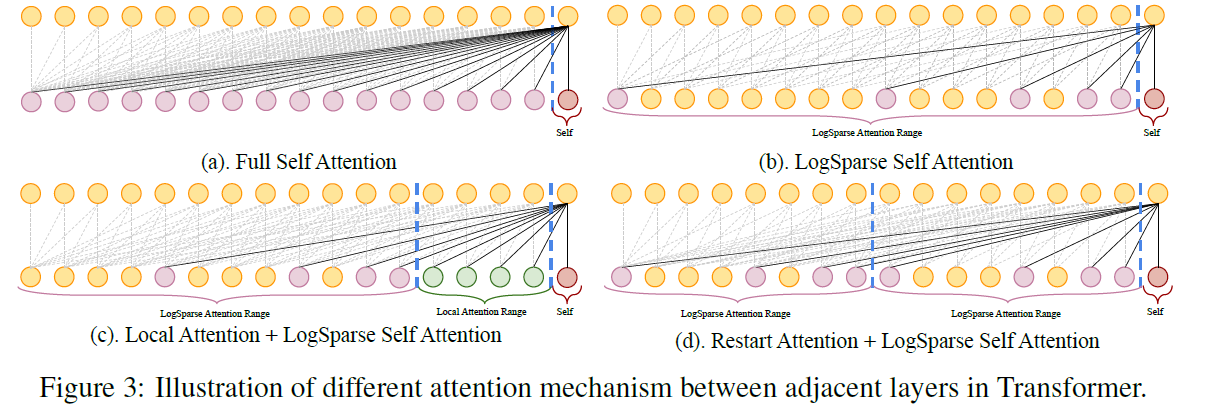
4. Experiment
(1) Synthetic datasets
$f(x)= \begin{cases}A_{1} \sin (\pi x / 6)+72+N_{x} & x \in[0,12) \ A_{2} \sin (\pi x / 6)+72+N_{x} & x \in[12,24) \ A_{3} \sin (\pi x / 6)+72+N_{x} & x \in\left[24, t_{0}\right) \ A_{4} \sin (\pi x / 12)+72+N_{x} & x \in\left[t_{0}, t_{0}+24\right)\end{cases}$.
- where $x$ is an integer,
- $A_{1}, A_{2}, A_{3}$ are randomly generated by Unif $[0,60]$
- $A_{4}=$ $\max \left(A_{1}, A_{2}\right)$ and $N_{x} \sim \mathcal{N}(0,1)$.
(2) Real-world Dataset
electricity-f( fine )electricity-c( coarse)traffic-ftraffic-c
