Conditional Time Series Forecasting with CNN (2017, 303)
Contents
- Abstract
- Introduction
- Model
- Structure
- Conditioning
0. Abstract
conditional MTS forecasting, based on convolutional WaveNet
- proposed network contains “stacks of dilated convolutions”
- capture correlation structure between MTS
- test on
- S&P500, Volatility Index, CBOE interest rate, exchange rates…
1. Introduction
main focus of this paper :
- MTS forecasting ( especially “financial” )
Characteristic of Financial TS
- 1) high noise component
- 2) changing financial environment
- 3) strongly correlated financial TS exist
Advantage of CNN over RNN
- # of trainable weights is small & more efficient
Contributions
- 1) present a CNN, inspired by WaveNet
- 2) successful in forecasting “Financial TS” with “Limited length”
- 3) time-efficient & easy to implement
- 4) experiments on various examples
2. Model
(1) Structure
consider 1-D time series : \(x=\left(x_{t}\right)_{t=0}^{N-1}\)
Task : predict \(\hat{x}(t+1)\), given \(x(0), \ldots, x(t)\)
Model : \(p(x \mid \theta)=\prod_{t=0}^{N-1} p(x(t+1) \mid x(0), \ldots, x(t), \theta)\).
- use CNN in the form of WaveNet
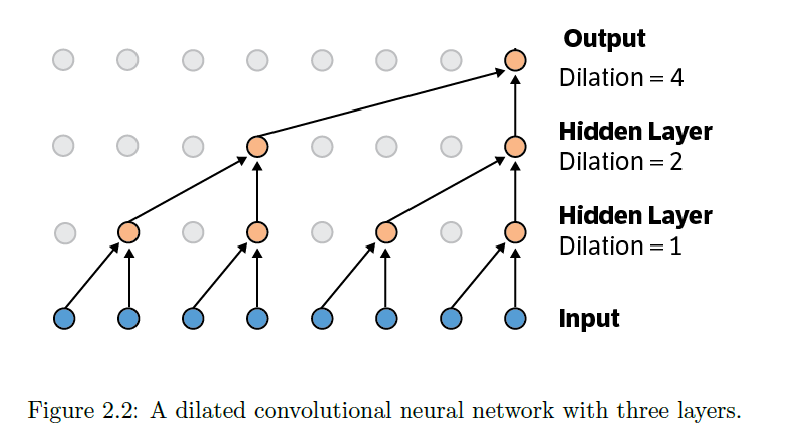
Idea of the network :
-
use the capabilities of CNN as “AUTOREGRESSIVE forecasting models”
( \(\hat{x}(t+1)=\sum_{i=1}^{p} \alpha_{i} x_{t-i}+\epsilon(t)\) )
Objective Function
- minimize MAE & L2 reg
\(E(w)=\frac{1}{N} \sum_{t=0}^{N-1} \mid \hat{x}(t+1)-x(t+1) \mid +\frac{\gamma}{2} \sum_{l=0}^{L} \sum_{h=1}^{M_{l+1}}\left(w_{h}^{l}\right)^{2}\).
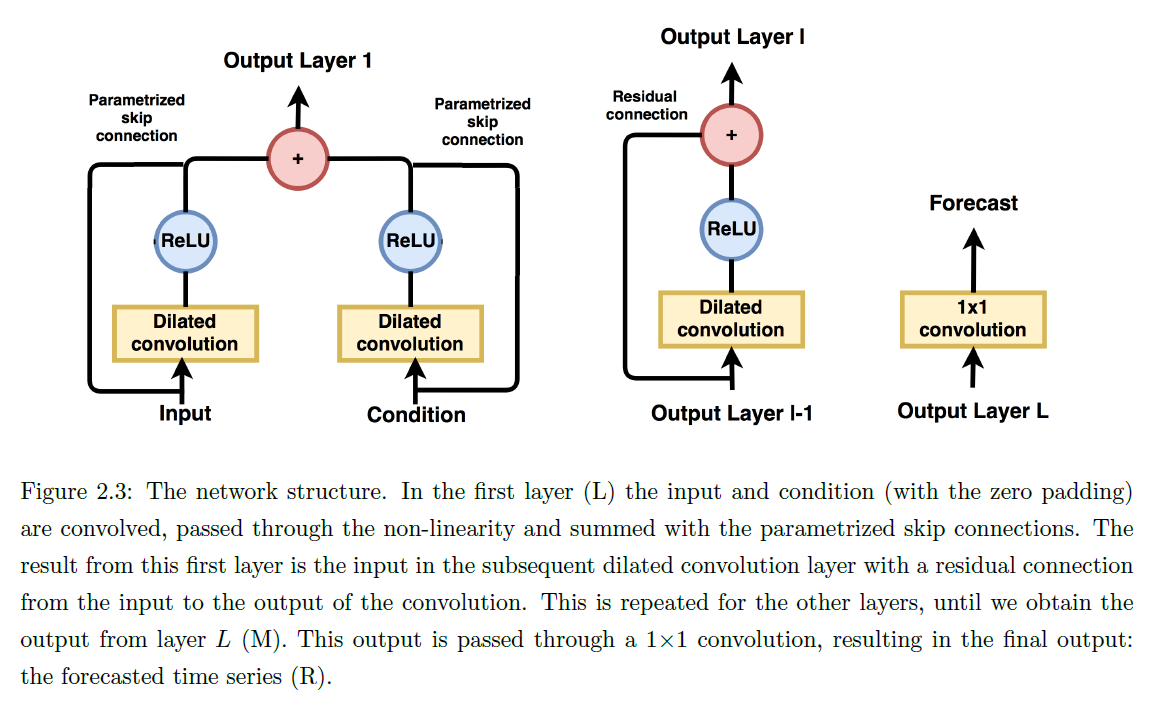
Residual Learning
add residual connection after each dilated convolution
(2) Conditioning
when forecasting (a) TS \(x\), conditioning on (b) TS \(y\)…
aim to maximize :
- \(p(x \mid y, \theta)=\prod_{t=0}^{N-1} p(x(t+1) \mid x(0), \ldots, x(t), y(0), \ldots, y(t), \theta)\).
Activation function + Convolution with filters \(w_{h}^{1}\) and \(v_{h}^{1}\) :
-
\(\operatorname{ReLU}\left(w_{h}^{1} *_{d} x+b\right)+\operatorname{ReLU}\left(v_{h}^{1} *_{d} y+b\right)\).
-
instead of residual connection in the first layer,
add skip connections parameterized by 1x1 conv