(paper) A Multi-Horizon Quantile Recurrent Forecaster

A Transformer-based A Multi-Horizon Quantile Recurrent Forecaster (2017, 137)

Contents

1. Abstract
2. Introduction
3. Related Works
4. Methodology
   1. loss function

   2. architecture

   3. training method

   4. encoder extension
   5. practical consideration

0. Abstract

Probabilistic Multi-step TS regression

• key 1) seq2seq
• key 2) Quantile Regression
• new training scheme : forking-seqeuences
• Multivariate
  • use both “temporal & static” covariates

Test on

• 1) Amazon.com
• 2) electricity price and load

1. Introduction

Goal :

• predict \(y_{t+1}\)
• given \(y_{: t}=\left(y_{t}, \cdots, y_{0}\right)\)

Many related time-series are present!

• ex 1) dynamic historical features
• ex 2) static attributes

most of models are built on “one-step-ahead” approach

• estimate \(\hat{y}_{t+1}\), given \(y_{: t}\)

• called Recursive Strategy

  ( = Iterative = Read-outs )

• problem : error accumulation

Direct strategy

• direclty predicts \(y_{t+k}\) given \(y_{: t}\)
• less biased / more stable / more robust
• Multi-horizon strategy
  • predict \(\left(y_{t+1}, \cdots, y_{t+k}\right)\)
  • avoid error accumulation
  • retains efficiency by sharing parameters

Probabilistic Forecast

• \(p\left(y_{t+k} \mid y_{: t}\right)\).

• traditionally achieved by assuming an error distribution ( or stochastic process )

  ( Gaussian, on the residual series \(\epsilon_{t}=y_{t}-\hat{y}_{t}\). )

• Quantile Regression

  • predict conditional quantiles \(y_{t+k}^{(q)} \mid y_{: t}\)
  • \(\mathbb{P}\left(y_{t+k} \leq y_{t+k}^{(q)} \mid y_{: t}\right)=q\).
  • robust ( \(\because\) no distributional assumptions )

MQ-R(C)NN

• seq2seq framework
• generate Multi-horizion Quantile forecasts
• \(p\left(y_{t+k, i}, \cdots, y_{t+1, i} \mid y_{: t, i}, x_{: t, i}^{(h)}, x_{t:, i}^{(f)}, x_{i}^{(s)}\right)\).
  • \(y_{\cdot, i}\) : \(i\) th target TS
  • 1) \(x_{: t, i}^{(h)}\) : temporal covariates ( available in history )
  • 2) \(x_{t:, i}^{(f)}\) : knowledge about the future
  • 3) \(x_{i}^{(s)}\) : static, time-invariant features

• each series : considered as one sample

  ( fed into single RNN / CNN )

• enables cross-series learning, cold-start forecasting

First work to combine RNNs & 1d-CNNs with QR or Multi-horizon forecasts

2. Related Work

[1] RNNs & CNNs

• point forecasting

[2] Cinar et al (2017)

• attention model for seq2seq

  on both UNIVARIATE & MULTIVARIATE ts

• but, built on Recusrive Strategy

[3] Taieb and Atiya (2016)

• multi-step strategies on MLP
• Direct Multi-horizon strategy

[4] DeepAR (2017)

• probabilistic forecasting
• outputs “parameters of Negative Binomial”
• trained by maximizing likelihood & Teacher Forcing

[5] MQ-R(C)NN

• more practical than relevant Multi-horizon strategy
• more efficient training strategy

3. Method

1. loss function

2. architecture

3. training method

4. encoder extension
5. practical consideration

(1) loss function

Quantile Loss :

• \(L_{q}(y, \hat{y})=q(y-\hat{y})_{+}+(1-q)(\hat{y}-y)_{+}\).
  • \((\cdot)_{+}=\max (0, \cdot)\).
  • when \(q=0.5\) : just MAE
• \(K\) : # of horizons of forecasts
• \(Q\) : # of quantiles of interest

\(\hat{\mathbf{Y}}=\left[\hat{y}_{t+k}^{(q)}\right]_{k, q}\) :

• \(K \times Q\) matrix
• output of of parametric model \(g\left(y_{: t}, x, \theta\right)\)

Total Loss : \(\sum_{t} \sum_{q} \sum_{k} L_{q}\left(y_{t+k}, \hat{y}_{t+k}^{(q)}\right)\)

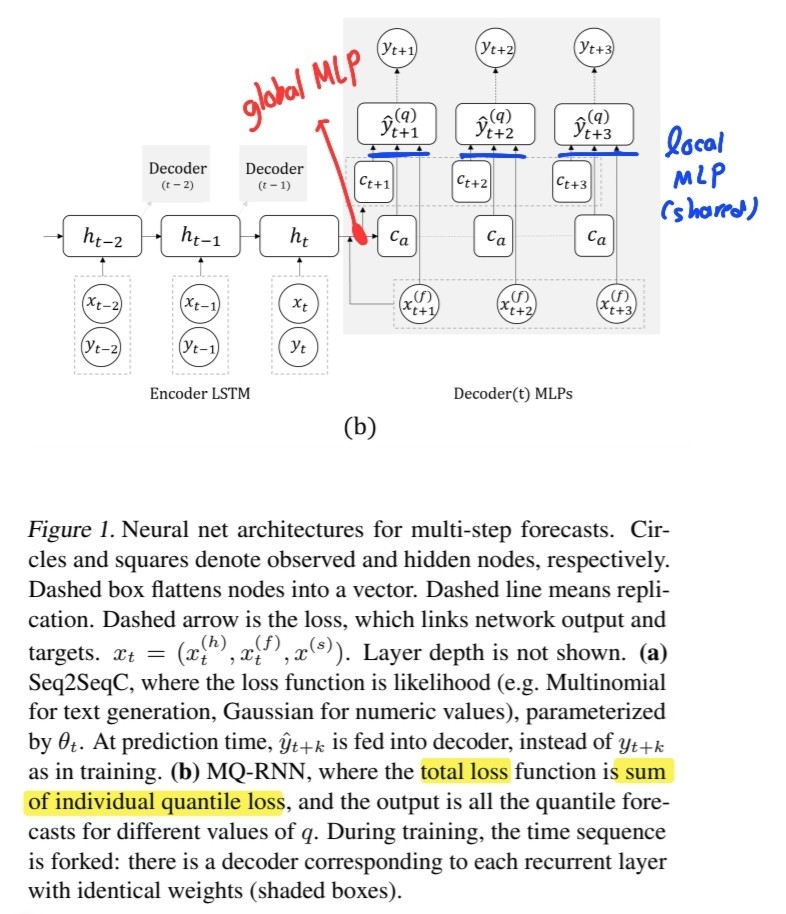
(2) architecture

• base : RNN seq2seq
• encoder : LSTM
• (recursive) deocder :2 MLP branches
  • 1) (global) MLP
  • 2) (local) MLP

1) (global) MLP

• \(\left(c_{t+1}, \cdots, c_{t+K}, c_{a}\right)=m_{G}\left(h_{t}, x_{t:}^{(f)}\right)\).
• input : “encoder output” & “future inputs”
• output : 2 contexts
  • # 1) horizon-specific context : \(c_{t+k}\) ( for each \(K\) future points )
  • # 2) horizon-agnostic context : \(c_a\)

2) (local) MLP

• \(\left(\hat{y}_{t+k}^{\left(q_{1}\right)}, \cdots, \hat{y}_{t+k}^{\left(q_{Q}\right)}\right)=m_{L}\left(c_{t+k}, c_{a}, x_{t+k}^{(f)}\right)\).

• applies to each specific horizon

• parameters are shared across all horizons \(k \in\{1, \cdots, K\}\)
• generate sharp & spiky forecats
• tempting to use LSTM, but unnecessary & expensive!

(3) training method

Forking-sequences training scheme

• endpoint
  • where ENC & DEC exchange
  • also called FCT(Forecast Creation Time)
  • time step where future horizons must be generated
• mathematical expression
  • 1) encoder : LSTM
    • \(\forall t, h_{t}=\operatorname{encoder}\left(x_{: t}, y_{: t}\right)\).
  • 2) decoder : global/local MLPs
    • \(\hat{y}_{t:}^{(q)}=\operatorname{decoder}\left(h_{t}, x_{t:}^{(f)}\right)\).

Direct strategy :

• criticized as not being able to use data between \(T-K\) & \(T\)
• thus, mask all the error terms after that point

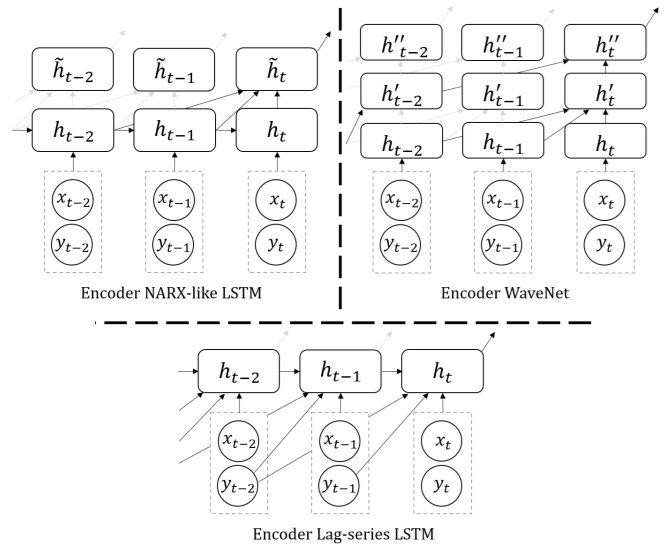
(4) encoder extension

many forecasting problems have long periodicity ( e.g 365 days)

& suffer from memory loss

NARX RNN

• compute hidden state \(h_t\),

  • not only based on \(h_{t-1}\)

  • but also \((h_{t-2},...h_{t-D})\)

    ( = skip connection )

• put an extra linear layer on top of LSTM to summarize them

  • \(\tilde{h}_{t}=m\left(h_{t}, \cdots, h_{t-D}\right)\).

Lag-seires LSTM

• feed past series as lagged feature inputs
  • \(\left(y_{t-1}, \cdots, y_{t-D}\right)\).

WaveNet

• not restricted to RNN
• WaveNet : stack of dilated causal 1d-Conv

(5) future & static features

[1] Future Features

• [1-1] seasonal features
• [1-2] event features

[2] Static Features