(paper) Neural Decomposition of TD data for Effective Generalization

Neural Decomposition of TD data for Effective Generalization (2017,40)

Contents

1. Abstract
2. Introduction
3. Related Works
   1. Models for TS prediction
   2. Harmonic Analysis
   3. Fourier NN
4. Neural Decomposition

0. Abstract

Neural Decomposition (ND)

• NN for “analysis” & “extrapolation” of time-series data

• use 2 kinds of units

  • 1) Units with “sinusoidal activation function”

    ( perform Fourier-like decomposition )

  • 2) Units with “non-periodic activation function”

    ( to capture linear trend & other non-periodic components )

1. Introduction

Analyzing time series data 2 ways :

[ approach 1 ] interpretation

interpret TS as a signal & apply Fourier transform to decompose it into a sum of sinusoids

• Fourier transform = uses a pre-determined set of sinusoid frequencies ( DO NOT LEARN )

  \(\rightarrow\) effective at interpolation, but bad at extrapolation

[ approach 2 ] regression & extrapolation

use models, such as NN

• Fourier NN : “sinusoidal activation functions”

  \(\rightarrow\) but, difficult to train

• RNN : difficulty in handling unevenly sampled TS

Proposal : ND

effective generalization can be achieved by…

• regression & extrapolation, using a model with 2 properties!

2 properties

• 1) combine both PERIODIC & NON-PERIODIC components
• 2) must be able to TUNE its components & weights ( = learnable )

Neural Decomposition (ND)

• 1) like Fourier Transform….
  • decompose signal into sum of constituent parts
• 2) unlike Fourier Transform….
  • able to reconstruct a signal “that is useful for extrapolating”
  • does not require the number of samples to be a power of two
  • does not require that samples be measured at regular intervals
• 3) includes “non-periodic” components
  • ex) linear, sigmoidal components
  • account for trends & non-linear irregularities

2. Related Works

(1) Models for TS prediction

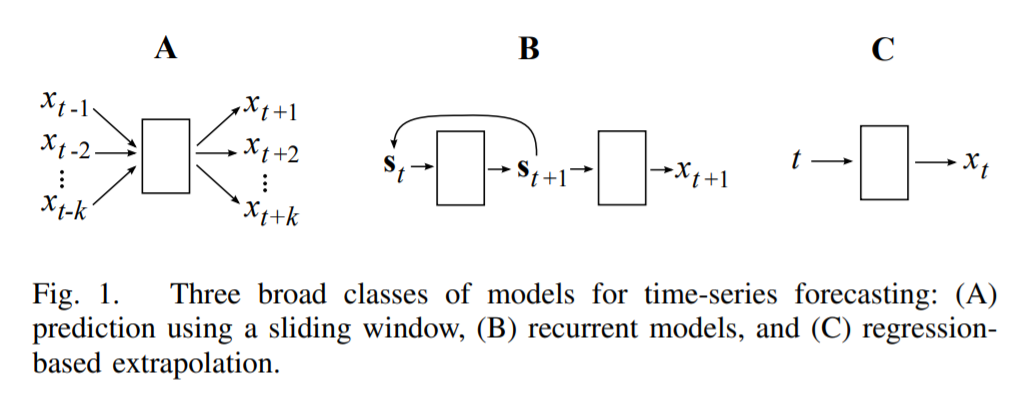
ND falls into (C) regression-based extrapolation

• fit a curve to a data & predict new data using the trained curve

• advantage over RNN

  • can make continuous predictions

• closely related to Fourier NN

  ( due to its use of “sinusoidal activation functions” )

(2) Harmonic Analysis

Harmonic Analysis of signal

( = Spectral analysis, Spectral density estimation )

• transform a set of samples from “TIME” domain \(\rightarrow\) “FREQUENCY” domain
• Interpolation & Extrapolation
  • ( interpolation ) able to reconstruct the original signal
  • ( extrapolation ) able to forecast values beyond the sampled time window
• ex) DFT (Discrete Fourier Transform)

DFT & iDFT

• ( DFT ) time \(\rightarrow\) frequency

  • use “negative multiples of \(2\pi / N\)” as frequencies

• ( iDFT ) frequency \(\rightarrow\) time

  • can be used as a continuous representation of the originally discrete input
  • use “positive multiples of \(2\pi / N\)” as frequencies
  • contains normalization term \(1/N\)

• written as a sum of \(N\) complex exponentials

  ( in terms of sines & cosines )

iDFT

Notation

• \(R_k\) : “REAL” components of \(k\)th complex number, returned by DFT
• \(I_k\) : “IMAGINARY” components of \(k\)th complex number, returned by DFT
• \(2\pi k /N\) : “frequency” of \(k\)th term
  • first frequency ( \(k=0\) ) : bias ( \(\because\) \(cos(0)=1\), \(sin(0)=0\))
  • second frequency ( \(k=1\) ) : single wave
  • third frequencey ( \(k=2\) ) : two waves
  • …
• cosine with \(k\)-th frequency : scaled by \(R_k\)
• sine with \(k\)-th frequency : scaled by \(I_k\)

Summary :

• sum of \(N/2 +1\) terms, with \(sin(t)\) & \(cos(t)\) in each term

• \(x(t)=\sum_{k=0}^{N / 2} R_{k} \cdot \cos \left(\frac{2 \pi k}{N} t\right)-I_{k} \cdot \sin \left(\frac{2 \pi k}{N} t\right)\).

  \(\rightarrow\) useful as a “continuous representation” of the real-valued discrete input

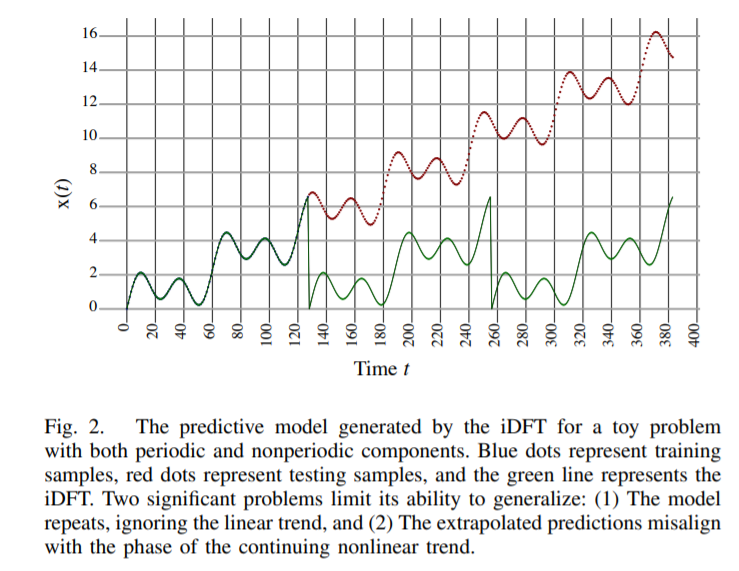
Problem :

• iDFT assumes …. \(x(t+N)=x(t)\) for all \(t\)
• cannot effectively model the “non-periodic components of a signal”

(3) Fourier NN

Fourier NN = NN that use a Fourier-like neuron

• case 1) input = Fourier transform of some data
• case 2) weight = Fourier transform

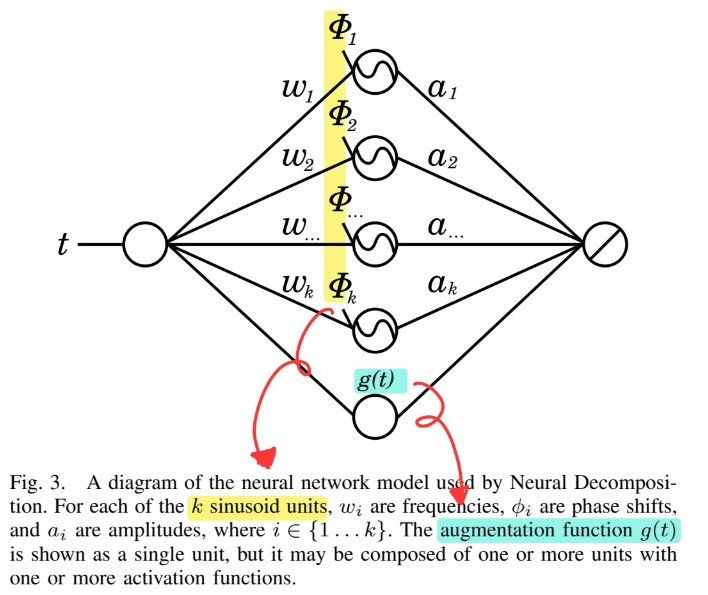
3. Neural Decomposition

describe ND (Neural Decomposition) for analysis & extrapolation of TS data

1. allow sinusoid frequencies to be TRAINED
2. augment the sinusoids with a NON-PERIODIC FUNCTION, to model non-periodic components

Notation

• \(a_k\) : amplitude

• \(w_k\) : frequency

• \(\phi_k\) : phase shift

• \(g(t)\) : augmentation function

  ( = represents the non-periodic components of the signal )

Model

• \(x(t)=\sum_{k=1}^{N}\left(a_{k} \cdot \sin \left(w_{k} t+\phi_{k}\right)\right)+g(t)\).
• comparison with iDFT
  • (1) \(k=0\) \(\rightarrow\) \(k=1\)
    • no need for bias term ( now, we have \(g(t)\) )
  • (2) \(N/2\) \(\rightarrow\) \(N\)
    • \(N/2\) sines & cosines each \(\rightarrow\) \(N\) sines only